（1）对于核电厂关键的SSC进行脆弱性评估（FA）时，需用到如下信息：

●SSC设计的布置图纸与计算书

●SSC抗震设计准则与规程

●抗震鉴定（试验或分析）报告

●重要的SSC有关设计规格书、管道和仪表系统详细布置图

●常用的脆弱性数据

●系统与部件在SSE下的设计反应谱

（2）SSC的HCLPF值可根据如下方法中的一种加以确定：

●概率脆弱性分析（PFA）

●保守的确定论失效裕度法（CDFM）

●抗震鉴定试验结果

●确定论方法

●常规的脆弱性数据

这里重点简述第1种PFA方法。

如脆弱性分析（FA）方法中采用概率论方法计算时，可得到重要SSC完整的易损度分布，如对部件进行地震峰值加速度承载值计算时，需考虑到保守性和随机性的众多不确定性因素，则HCLPF值反映具有“高置信度和低概率失效”准则，即从中可反映不超过5%的失效概率具有95%的置信度。而HCLPF值一般可通过对数正态概率分布加以定义的，该对数正态概率分布是地震承载中值Am与复合标准差βc的函数：

式中，Am为地震承载的中值，βc=为复合标准差，βR为地震随机不确定性的综合标准差，βv为SSC模型不确定性的综合标准差。

地震承载中值Am与地震承载均值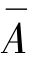之间关系为

地震承载均值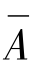与应力、强度设计裕量因子之间关系为

式中，A0为以地震地面加速度峰值计及的承载名义值，Xi为第i个设计平均裕量因子（i=1，2，…，N）。

复合标准差βc等于各个裕量因子Xi相关标准差βi的均方根值，即可表示为

由式（6.6.1）～式（6.6.3），HCLPF可表示为

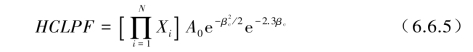
式中，A0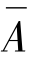， ，Am的单位均可用重力加速度g来表示（9.81 m/s2）。(www.daowen.com)

裕量因子Xi的基本种类包括确定性强度因子、可变强度因子、材料阻尼比、非弹性的能量吸收（延性）、分析或模型误差、±结构相互作用（SSI）等方面。如确定HCLPF值的部件，其对于SSE的阻尼比可取表6.6.1中的值。

表6.6.1　不同部件SSE下的阻尼比

（续表）

注：超过屈服强度变形的部件，可取等于7%或更高。

又如分析误差类中为了反映用于计算地震承载的动态振型模型中的建模误差，SMA分析中可计及分析误差产生的标准差为

（3）概率脆弱性曲线。

根据式（6.6.1）给出求解HCLPF值的概率脆弱性公式以及它们的对数正态分布假设，可以计算一组近似表达脆弱性不确定性的概率脆弱曲线。给定峰值地面加速度（PGA）a与条件失效概率f0的关系式为

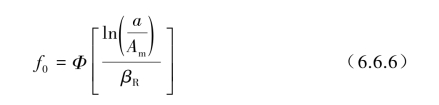
式中，Φ［·］为标准高斯正态概率分布函数，表达式为Φ（x）=

如果也考虑SSC模型随机不确定的综合标准差的话，该脆弱性曲线可由两组复合随机不确定标准差来表示。在任意峰值地面加速度值作用下，脆弱性条件失效概率f′均可以由重合概率密度来表达。式中，Q=P［f＜f′|a］为PGA=a时的条件概率f＜f′的置信度值，Φ-1［·］为标准高斯正态概率分布反函数。

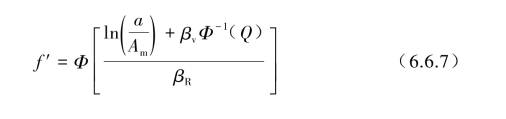
例如某部件的地面加速度中值Am=0.67g，βR=0.25，βv=0.35，其条件失效概率f0和a关系的PFA曲线如图6.6.1所示。

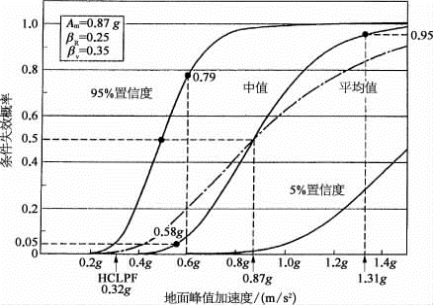
图6.6.1　部件的均值、中值、5%和95%不超越失效概率（置信度）的脆弱性曲线

当PGA=0.6g时，由式（6.6.7）计算出具有95%条件失效概率f′=0.79，即在图6.6.1中由95%置信度的曲线所示。失效概率在5%～95%置信度区间内的f′变化范围为0～0.79。图6.6.1还给出了由式（6.6.6）得到的平均概率脆弱性曲线和中值概率脆弱性曲线。

中值Am=0.87g，βc==0.43，按式（6.6.1）可计算出HCLPF=Ame-2.3βc=0.32g。

当条件失效概率中值（即置信度）从5%变化到95%时，其地面加速度的对数正态概率分布是±1.65倍综合标准差βR的函数，即地面加速度峰值将从Ame-1.65βR变化到Ame1.65βR，在图6.6.1中的中值曲线上，求得a=（0.58～1.31）g。

（4）特例。

某核电厂一次侧部件进行PFA评估得到的Am，βc和HCLPF值如表6.6.2所示。

表6.6.2　一次侧部件PFA结果

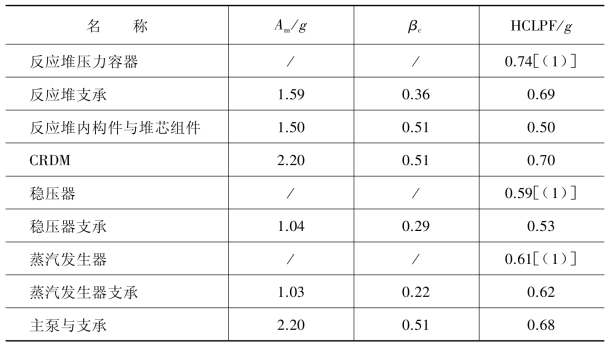
注（1）：基于确定论法。