核电厂构筑物、系统和部件抗震分析最常用的方法为：反应谱法、模态叠加法与时程分析法3种分析方法。

1）反应谱法

大多数核电厂抗震设计规范中，采用反应谱法来确定地震作用，其中以加速度反应谱应用为最广泛。3.3.4节专门论述了地面反应谱的基本概念、如何从地面输入求得反应谱以及地震楼面反应谱的生成技术，图6.3.5的核电厂SSC抗震设计分析流程图清楚表征了在反应谱分析方法中如何应用获得的楼面设计反应谱作为地震分析的输入。反应谱法先以动力分析方法求得设备的动态特性（包括各阶固有频率及振型）后，在设备支承位置处所对应的设计楼面加速度反应谱上查到每阶固有频率所对应的加速度反应值，再在设备上施加每阶的等效加速度值，采用静力法分别求解每阶模态的反应，包括位移、内力、内矩或应力，然后最终将各阶的反应组合成总反应。

例如某单跨直梁或多质点自由度系统在支承处有一地震加速度时程输入时（见图6.3.7），其模态振动反应方程同式（5.5.69）。

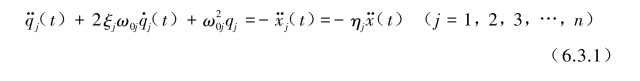
式中，ω0j，ξj为第j阶模态固有频率和模态阻尼比；为第j阶模态相对于支承的模态位移、速度和加速度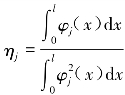；为振型参与系数，为第j阶梁模态振型函数，x和l为梁上距离长度和跨长度。

图6.3.7　多自由对振动系统在基础上地震输入

式（6.3.1）是表征了多自由弹性体系分解为第j阶模态下的一个标准单自由度振动方程。式（3.3.57）是式（3.3.6）的特解，也是制作相对位移、相对速度和绝对加速度最大峰值反应谱Sd（ξ，ω0），Sv（ξ，ω0）和Sa（ξ，ω0）的表达式。

模态振动方程式（6.3.1）与式（3.3.6）比较可清楚看出，从分解为第j阶模态振动方程后两者从单自由振动方程出发完全是等效的，不同的是，在（6.3.2）反应谱中参数需用第j阶（ξj，ω0j）参数代入，并差一个模态参与系数ηj的倍数，当已知梁在基础A和B支承处有一设计楼面反应谱Sd（ξ，ω0），Sv（ξ，ω0）或Sa（ξ，ω0）输入时，对应梁各阶模态位移、速度和加速度最大峰值则与式（6.3.2）相对应，可得到如下倍数关系。

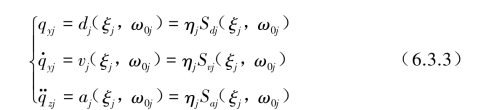
式中，qyj，为第j阶模态振型下的相对位移、速度和加速度，脚标y，z表示相对和绝对的含义，其中

梁上各坐标点x上总的相对位移w（x）、相对速度和绝对加速度则由式（5.5.71）和式（6.3.3）得到。

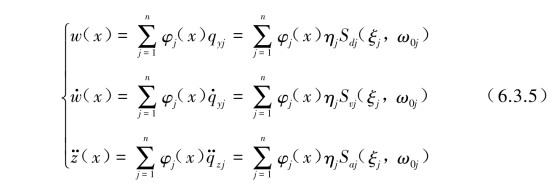
梁各截面上的法向弯矩和法向弯曲应力由式（5.5.72）和式（6.3.3），并应用近似关系Sdj（ξj，ω0j）≈Saj（ξ，ω0j）/ω0j后得到

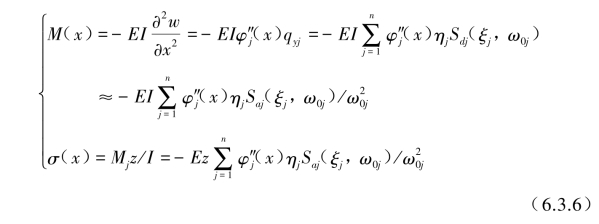
对于模态组合结果式（6.3.5）和反应式（6.3.6）可清楚看出反应谱方法与5.5节中模态叠加法相同之处是都需要求解结构的模态频率、阻尼、振型、参与系数等特性。但反应谱方法最本质的区别是当结构的模态位移、速度和加速度由反应谱直接求得后，由静力方法直接求得结构中的内力（或内矩）与应力，而模态叠加法的求解模态位移、速度和加速度以及内力和应力的全过程均采用动力法，可认为这是时程法中的一种特定的方法。

所以在了解了反应谱方法的实质后，可清楚看出式（6.3.5）和式（6.3.6）中所有qyj，值不是时间t的函数，而是直接取自单自由度系统中反应的最大峰值，因此总输出也按式（6.3.5）和式（6.3.6）中各个模态最大峰值的线性组合，其结果将会十分保守，甚至不可信，为此在工程中采用常规处理每个方向上的模态反应的组合可表示为

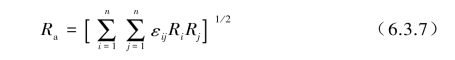
式中，Ra为总的模态反应；n为重要模态的总数；Ri=Aiψi为第i阶模态的反应，Rj=Ajψj为第j阶模态的反应，Ai，Aj分别为第i阶、第j阶模态的振型系数，ψi，ψj分别为第i阶、第j阶模态的振型；εij为耦合系数或互相关系数。

ψi和ψj可以是位移、反力或应力所对应的振型。Ri和Rj也可以是位移、反力或应力所对应的反应。

其组合方法主要有以下3种：

（1）平方和开根（SRSS）组合方法。

所有的模态不相互耦合时，式（6.3.7）为

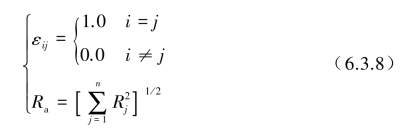
（2）双和（DS）组合方法。

式（6.3.7）变为

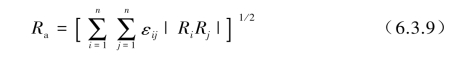
式中，εij=　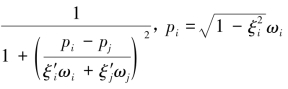为第i阶模态下有阻尼的固有圆频率，ωi，ξi分别为第i阶模态无阻尼下固有圆频率和阻尼比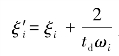，为第i阶模态的修正模态阻尼比，td为地震持续时间。

（3）完全二次项（CQC）组合方法。

其组合反应表示为

式中，k=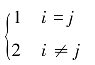　

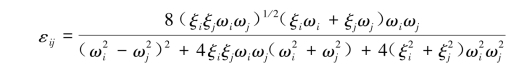
ξi，ωi分别为第i阶的模态阻尼比与无阻尼固有圆频率。

其他组合方法可参见文献［19］。

对于两个水平和一个垂直方向的模态反应，可将各个模态反应按上述方法之一进行组合后，3个方向激励的总的组合反应可表示为

式中，k=1，2，3表示地震3个主方向，如两个水平和一个垂直方向。

另外也可接受的方法为百分比组合，对于|R1|≥|R2|≥|R3|时，

R=1.0|R1|+0.4|R2|+0.4|R3|

（6.3.12）

反应谱方法分析时需注意几点：

（1）由动力法求解结构的模态特性（固有频率、振型等）后，从输入的设计反应谱上获得对应的反应值，再由静力法求解各阶模态的位移、反力、内力、内矩和应力。

（2）再由式（6.3.7）对各种反应进行组合得到各点上的总反应值。

（3）对结构上各个截面的应力分解（Pm，Pb，Q，F）是由各阶模态中分别求得的，所得到总的应力分解值也是按式（6.3.7）分别求得Pmj，（Pm+Pb）j，（Pm+Pb+F）j后进行组合，得到总Pm，Pm+Pb，Pm+Pb+Q和Pm+Pb+Q+F值。而不是在截面上的最终组合应力分量结果上进行应力分解。

（4）当结构多点支承处有不同反应谱输入时，可保守地用包络各输入反应谱作为输入，也可用其他适用的方法。

（5）特别注意结构上所得到的位移值均是相对于不动支承处的相对位移。

［例］ 简支梁尺寸与材料参数（见图6.3.8）为

L=10 m，b=0.05 m，h=0.1 m，E=2×1011 N/m2，ρ=7.8×103 kg/m3，ξ=4%

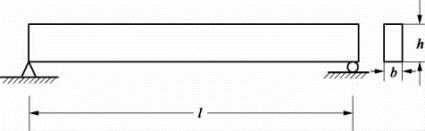
图6.3.8　简支梁尺寸(www.daowen.com)

解：两端简支梁的齐次特征方程与振型为

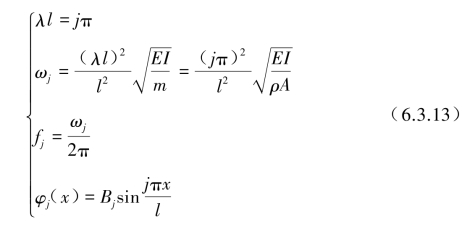
图6.3.9为支承上输入的地震设计加速度楼面反应谱。

（1）求梁模态固有频率与振型。

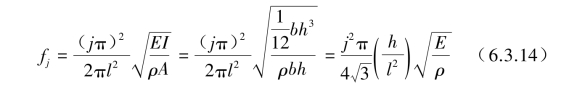
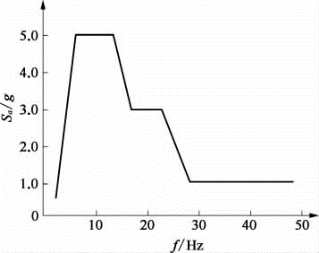
图6.3.9　地震设计加速度楼面反应谱

将E，ρ代入fj得

将h和l代入后得前5阶固有频率，如表6.3.2所示。

表6.3.2　前5阶固有频率

设振型φj（x）的系数Bj=1

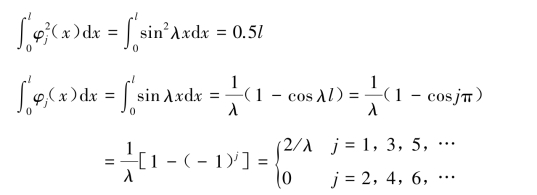
振型参与系数ηj为

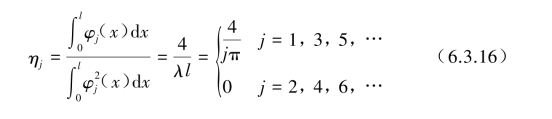
（2）求解各阶模态的最大位移和最大应力。

由式（6.3.4）求解作用在梁垂直方向上的线分布力，对于每阶模态所对应参数值和计算结果如表6.3.3所示。

表6.3.3　各阶模态所对应的参数

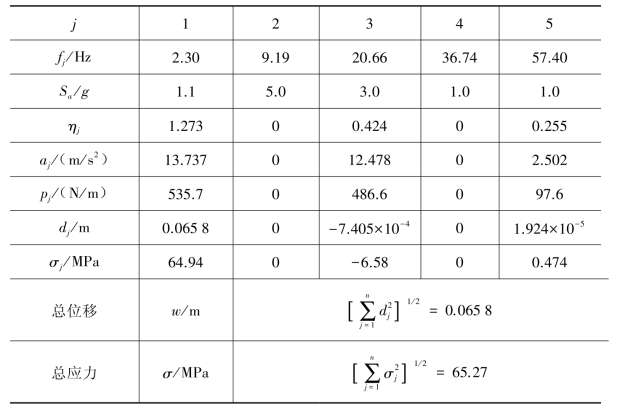
表6.3.3中的每阶模态的最大位移和最大作用分布力的计算式为

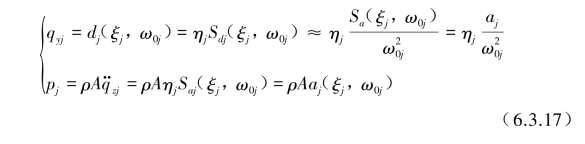
由式（6.3.6）求得每阶模态弯曲应力最大值为

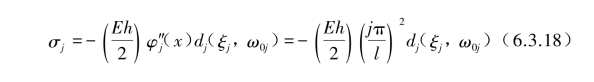
梁上各点x对应的总位移w（x）和总弯曲应力σ（x）为

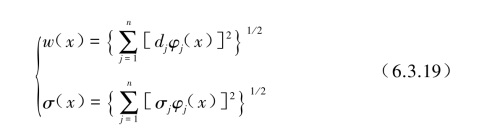
（3）应力分类。

由式（6.3.18）计算的各阶模态下的应力σj应归属为一次弯曲应力强度（Pb）j=σj，而由式（6.3.19）所计算的总应力σ则为总一次弯曲应力强度Pb=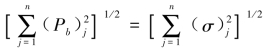。各个应力强度分类计算值如表6.3.4所示。

表6.3.4　应力强度分类表

2）时程法

时程法包括模态叠加分析方法和全瞬态动力分析方法两种，与反应谱方法最本质区别是，它是全程与时间t有关的动态分析方法。

（1）模态叠加法是多步、时间步长的线性分析，该解法先是采用与反应谱方法相同的模态分析求解各阶模态，然后再由各阶模态时程分析，求得各阶模态位移、速度、加速度及应力，再线性叠加起来计算结构总响应，包括位移、速度、加速度及应力等反应。该基本理论详见5.4节。

对于地震分析常见的具有间隙支承的结构抗震分析，简化为模态叠加法是十分有成效的，读者可参考附录G。

（2）全瞬态动力分析方法是使用振动方程的全质量阵M、阻尼阵C和刚度阵k。它具有完整的非线性求解功能，在抗震分析中的重要设施，需要求解结构各处所需的楼面反应谱时采用该方法。另外，如不同支承处有不同的地震位移时程输入时也可应用该方法求解其反应，由于每个支承产生不同的运动，结构系统的反应可包括质量点上的惯性效应以及支承之间差异运动引起位移差等两种反应。具体如何分解可按如下步骤进行。

多自由度动力方程可表示为

式中，M，C，K分别为系统质量、阻尼和刚度矩阵，z··为质量点上的绝对加速度，y=z-x为节点上相对于支承激励处的相对位移。

假设系统内其中有一个支承认为是“基准支承”的不动点，则其余支承可作为基准支承的相对运动来描述，式（6.3.20）可分解为式中，Mm为系统集中质量矩阵；Ms为与系统相连支承惯性项的质量矩阵，如支承连接无质量时，认为Ms=0；Cm，Cs分别为集中质量点和支承点的阻尼矩阵；Kmm为质量有关的刚度矩阵；Kss为支承有关的刚度矩阵；Kms，Ksm分别为质量点与支承之间的耦合刚度矩阵；为质点动态自由度的绝对加速度；为支承点上的绝对加速度；ym为每个坐标方向上相对于基准支承点的位移；ys为非基准支承相对于基准支承点的位移；Fm为作用在质量点上的外力；Fs为作用在支承点上的外力。如仅仅在支承上输入位移时，则可以设Fm≡Fs≡0。

对于非基准支承上的支承运动应只计及系统产生变形（或应力）的支承位移，对于刚性平动或刚性转动不会产生变形的应通过非基准支承相对运动方法给予去除。

ys=（xs-xd）-Rsθsd

（6.3.22）

式中，xs为每个激励方向上非基准支承点的绝对位移（输入），xd为每个激励方向上基准支承点的绝对位移（输入），Rs为基准支承点与非基准支承点之间距离的3个正交矢量矩阵，θsd为支承结构绕三个坐标上每个轴的刚体转动（相对输入）。

式（6.3.21）中第1个方程可表示为

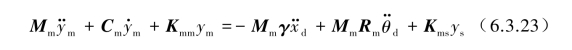
式中，xd，分别为基准点每个坐标方向上的绝对位移、速度和加速度，θd，分别为基准点每个坐标方向上的绝对转动、角速度和角加速度，Rm为基准支承点到质点之间每个转动分量距离矩阵，γ为每个自由度平动的方向矩阵。

式（6.3.23）左端表示系统相对于基准支承的动态3个自由度上惯性力、阻尼力和刚度力的合成，其右端表示相对于基准支承上的地震加速度产生的外力等效作用在系统上，其等效外力包括基准支承上平动加速度x··d和转动加速度所产生的等效惯性力，以及非基准支承相对于基准支承之间相对位移ys所产生的等效刚度力（-Kmsys）。

这两部分可以分别等效作用，图6.3.10为其典型的分解方法，第1部分作用在系统质点上，第2部分作用在非基准支承上，由式（6.3.17）分别求出其反应后，其第1部分所引起的应力可视为一次应力（Pm，Pm+Pb）。第2部分所引起的应力可视为二次应力（Q），分别与其他载荷组合后给予应力强度评定。

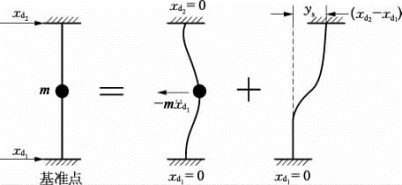
图6.3.10　典型支承激励的分解

这里值得注意的是，从图6.3.10中支承点运动可清楚看出，即使两处支承在水平方向以相同幅值和频率的绝对位移做同步运动时，在集中质量m处仍然会产生惯性效应的运动，这时在结构中所产生的应力将视为一次应力。

全瞬态动力方法求解方程式（6.3.23）可基于Newmark直接积分法和Newton-Raphson方法，具体步骤求解方法可参考有关资料。