1）强迫振动模态方程与解

设单跨梁的刚度为均布EI，单位长度质量也为均布ρA，跨长为L，截面积为A。在梁的强迫振动下还需考虑材料阻尼效应，设内阻尼与应变速率成正比，即梁的轴向应力式（5.5.3）可转化为

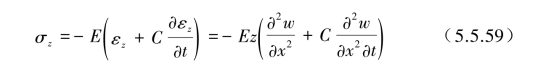
梁的振动方程式（5.5.7）则变为

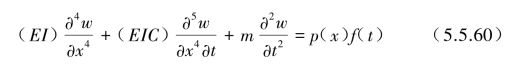
方程中p（x）为外载f（t）的沿梁长x上的无量纲分布函数，f（t）为作用在梁上的单位长度分布力（N/m）。

仍同式（5.5.9），将位移w（x，t）采用振型分离方法作分离：

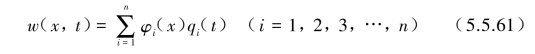
式中，φi（x）为梁的第i个模态振型函数，qi（t）为主坐标。将式（5.5.61）直接代入式（5.5.60），方程两边左乘振型函数φj（x）并对梁长0～l积分。则得

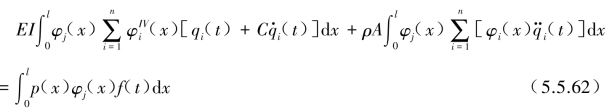
根据5.5.4节振型函数φi（x）的正交性质，由式（5.5.45）可知：

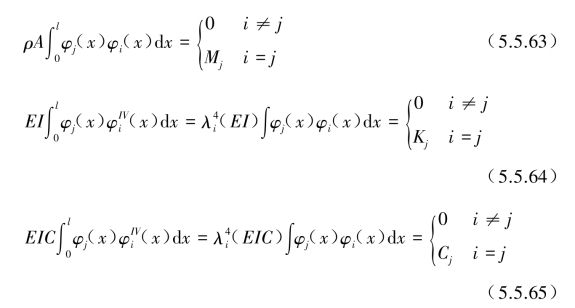
式中，Mj，Kj和Cj均定义为第j阶的模态质量、模态刚度和模态阻尼，代入式（5.5.62）后得到第j个模态独立的单自由度振动方程为

将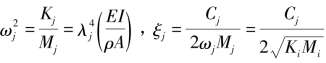分别代入标准单自由度振动方程得

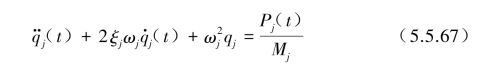
这里，模态质量、模态刚度、模态阻尼与模态力分别由梁振型函数φj（x）求得

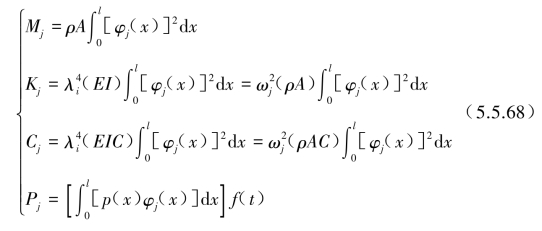
注意式（5.5.66）是针对外力p（x，t）直接作用在梁截面上，如果梁支承处有地震位移（或加速度）波形输入时，需要采用图5.4.1中关于地震基础输入的等效分析方法，即用替代式（5.5.66）中的Pj（t）。则模态正则方程式（5.5.67）改为类似式（5.4.6）的形式，由于假设各支承处的输入加速度是相同的，在梁上各点的输入加速度与位置x无关，因此分布函数p（x）=1。这时模态振动方程为

式中，为等效输入加速度，ηj为振型参与系数。

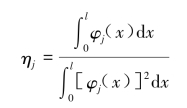
这里qj（t）是梁相对于基础支承运动xj（t）的位移，而梁的各位置上的绝对加速度应类似5.4.4节方法求得

式中，为第j阶模态振型下的输出绝对加速度，qyj（t）和则为第j个模态振型下的输出相对于基础xj（t）的位移与速度，即等于方程式（5.5.69）中的qj（t）的脚标改为yj。

则梁上各坐标点x上输出总的相对位移w（x，t）、相对速度和绝对加速度可表示为

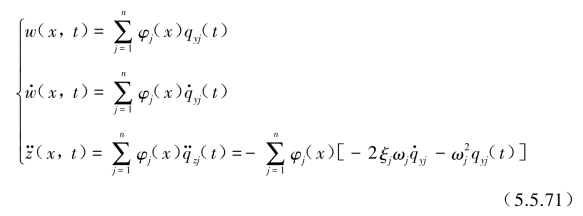
梁各截面上的法向弯矩和法向应力可由式（5.5.4）得到

模态方程（5.5.69）的解qyj（t），可按式（5.4.8）、式（5.4.9）或式（5.4.11）得到，则可由式（5.4.10）或式（5.4.11）求得，这里不再重复列出。

2）谐波激励的反应

当梁支承处输入时程加速度，如式（3.4.13）所示采用三角级数模型来模拟合成的人工地震波时，按式（5.5.69）右端项中可表示为

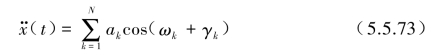(www.daowen.com)

式中，=4S（ωk）Δω=2G（fk）Δf，k=1，2，…，N。

S（ωk），G（fk），Δω，ωk和φk的含义均与式（3.4.14）和式（3.4.15）相同。

将代入式（5.5.69）可求得每个模态振型j的等效加速度为

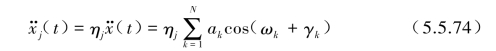
将式（5.5.73）代入式（5.4.11）单自由度强迫振动解，则可得到各模态解qyj（t），

从式（5.5.75）同样可看出qyj（t），结果均为3部分组成，第1部分属于纯初始条件所确定的自由振动反应项，由于阻尼比ξj使该时程很迅速衰减。第2部分属于伴随强迫振动反应项，此项也随时间增长而迅速衰减。第3部分才属于真正的强迫振动反应项，其反应按激励中圆频率ωk的谐振而变化。

当梁结构的某个或几个固有圆频率ωj与基础激励谐振圆频率ωk相等时，该系统会发生共振，将ωk=ωj与对应ak代入式（5.5.75）后得到共振状态下的解为

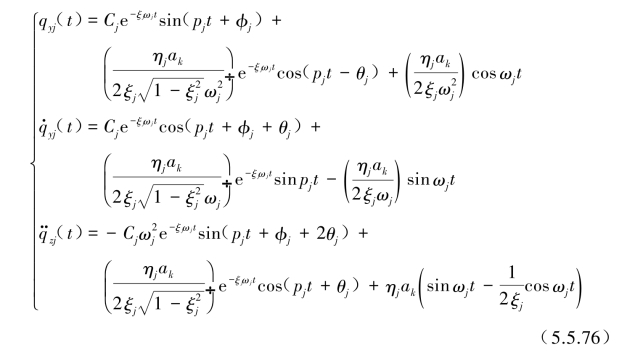
从上式结果可清楚看出，系统在共振时伴随强迫反应项与基础输入的谐振振幅值ak相比均放大了倍。将qyj（t），代入式（5.5.68），可得到梁位置x处上各个总的输出量，因各阶模态坐标中仅是第j阶模态的反应发生共振，可近似将共振ωj=ωk处的qyj（t），和中不随阻尼比衰减的第3部分单独取出，则w（x，t），和可表示为

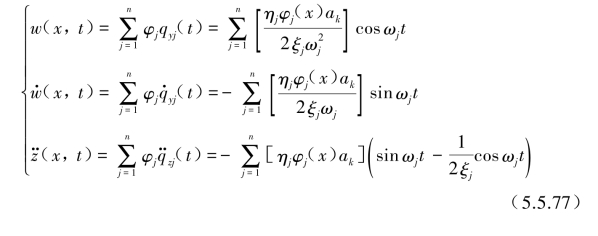
各截面上弯矩和轴向应力可表示为

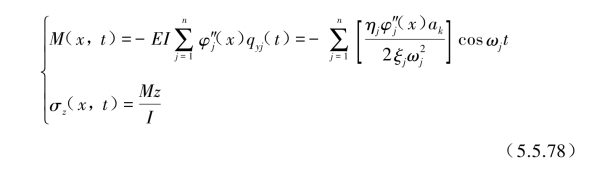
3）随机波激励的反应

当梁的支承处输入的加速度假设为一种随机信号波形时，即模态振动方程式（5.5.69）的右端项也可作为随机信号来处理，如果输入设为均值为零的平稳各态历经的高斯过程，其输入自功率谱密度为，则方程中每阶模态j对应的输出）的自功率谱密度按式（3.4.48）和式（3.4.54）表示为相对位移输出自功率谱密度为

式中，为各阶所对应的等效加速度自功率谱密度函数，ηj为式（5.5.69）所示的振型参与系数；ωj，ξj为梁各阶模态的固有圆频率的模态阻尼比；ω为输入自功率谱密度函数中的频率变量。

对于绝对加速度各阶模态输出自功率谱密度函数可由式（3.4.55）作转化。

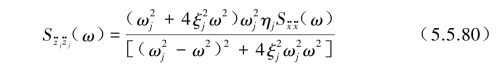
当梁的固有频率ωj互相离得较远，且阻尼比ξj很小情况下，可以假定各模态反应是统计上独立的。梁上任意点的位移w（x，t）功率谱密度函数Sw（x，ω）可认为各振型分量功率谱密度函数的线性组合，即

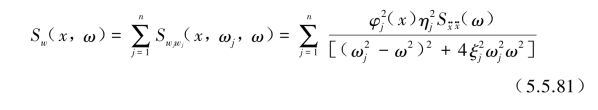
梁上任意点的绝对加速度功率谱密度函数为

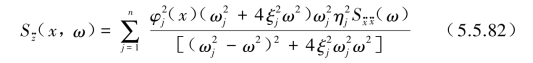
其输出相对位移w（x，t）和绝对加速度的均方值为

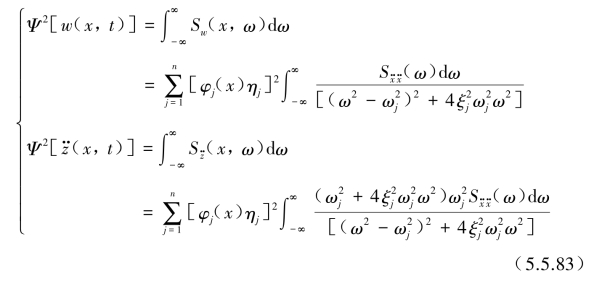
梁的轴向应力反应均方值为

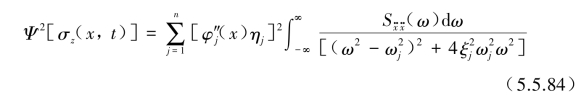
当输入加速度为一白噪声波形时，可知为常数，则输出可参照式（3.4.79）结果为的频带宽度比|H（jω）|2宽得多时，那么输入功率谱密度函数

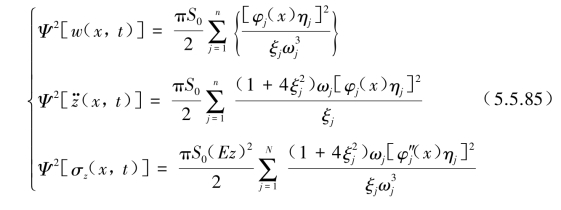
如果输入功率谱密度不是白噪声时，若就可以用共振点ω=ωj处的来替代，则输出的均方值可近似表示为

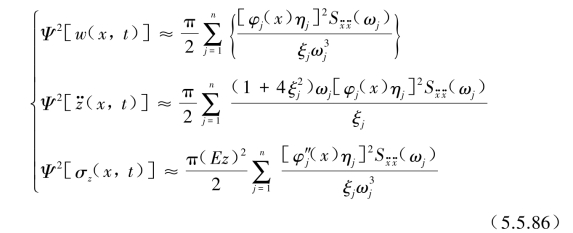
当振型阶数j增大时，上述的级数收敛很快，仅出现较低次的振型。另外，其反应均方值是坐标x的函数，在梁上如出现振型函数的节点时，将不会出现相应的反应值。