1）单跨简支梁在支承处弯矩作用下的振型

假设多跨梁的支持均为简支条件，如图5.5.6（a）和（b）所示，相邻两跨的支承上作用着数值相等、方向相反的弯矩，其中梁的一端作用弯矩Mν-1sin ωt，在梁的另一端作用弯矩Mνsin ωt。

图5.5.6　相邻两跨力矩平衡

由于梁上无其他干扰力，因此梁弯曲振动满足振型φ（x）方程：

φIV（x）-λ4φ（x）=0

（5.5.50）

其解为

φ（x）=Bsin（λx）+Ccos（λx）+Dsh（λx）+Ech（λx）

（5.5.51）

式中，λ与式（5.5.13）相同。

考虑图5.5.6（a）的简支边界条件，应用简支支承弯矩的条件，可列出边界条件为

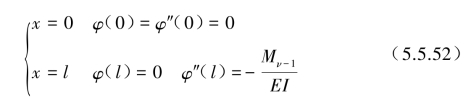
代入式（5.5.51）后得到

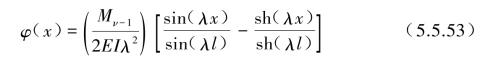
同理，考虑图5.5.6（b）的简支边界条件，可求得该梁上的振型为

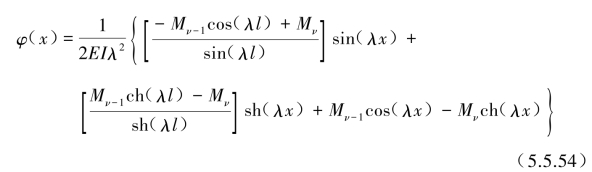
2）三弯矩方程

根据式（5.5.53）和式（5.5.54），可以得到连续梁自由振动的三弯矩方程。假定限于等截面等跨连续梁，所有ν支承上的弯矩Mν，由相邻两跨ν支承上的转角相等条件（见图5.5.7）可求得

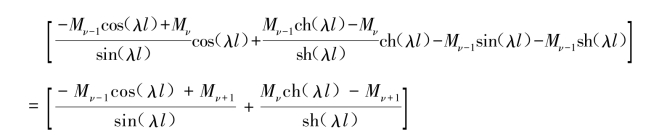
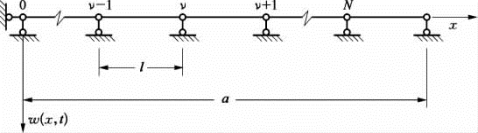
图5.5.7　连续梁支承标志号

整理后可得到连续梁自由振动的三弯矩方程为

ψMν-1+4θMν+ψMν+1=0

（5.5.55）

式中，(www.daowen.com)

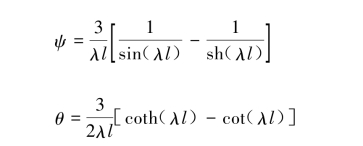
该方程表示了连续梁上每一个中间ν支承，都包含前（ν-1）和后（ν+1）两支承在内的Mν，Mν-1，Mν+1 3个弯矩。对于两端简支的连续梁，则可表示为N个线性代数方程。

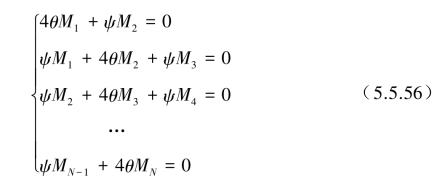
式中，N表示连续梁除两端处在中间的支座数，如两跨梁N=1；三跨梁N=2……

3）连续梁的自振圆频率求解

对方程式（5.5.56）的非零解为代数方程式的系数行列式等于零，即

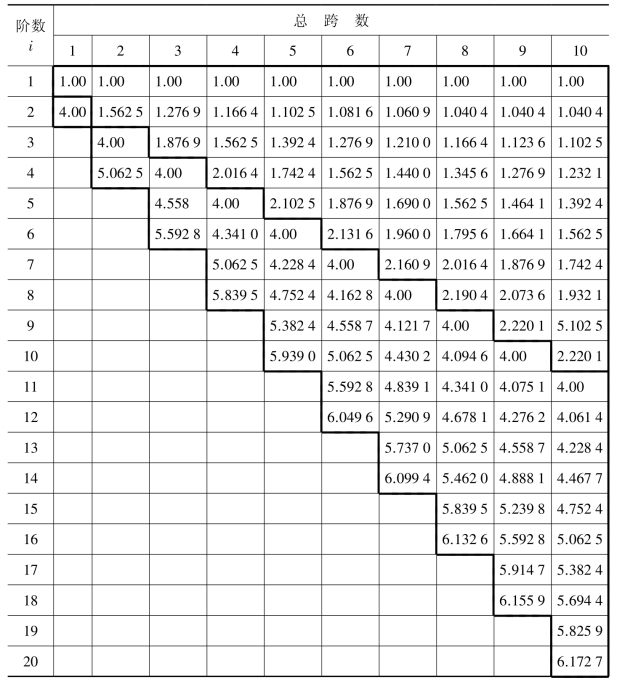
将行列式（5.5.57）展开后，可得出特征值λ的特征方程，便可求得λi（i=1，2，3，…），再由式（5.5.13）求得自振圆频率ωi，表5.5.4列出了1～10跨的连续梁，最高为20阶的固有圆频率比值。其中对所有跨数的第1阶固有圆频率ω1均设为ω1=1，其余i≥2的各阶ωi均为对ω1的比值（ωi/ω1）。从表中结果可清楚观察到以下现象。

（1）单跨简支梁第1阶ω1=1，第2、第3、第4阶以ωi=4，9和16…（i2）递增，且不存在频率密集区。

（2）多跨连续梁则不同，对应自振圆频率1～4之间还存在接近1的共振圆频率，称为第1频率密集区。在4～9之间存在接近4的共振圆频率，称为第2频率密集区。

（3）如果多跨连续梁各跨的跨长、刚度和质量相同，则对某个多跨梁每个密集区中相接近的共振圆频率数是相等的，且恰好等于该连续梁的跨数。

（4）每个密集区内所对应的频率范围基本上趋于恒定值，如第1密集区的频率范围从1.00～2.220 1，第2密集区的频率范围从4.00～6.172 7。且随着跨数的增加其范围趋于恒值。

（5）随着跨数N的增加，每个密集区内共振频率之间的间隔愈小，即邻近频率愈接近。如以10跨梁为例，（ω2/ω1）之比仅为1.040 4，（ω3/ω1）为1.102 5，也就是说跨数愈多，其密集区内的频率显得愈密集。

4）连续梁的振型φi（x）求解

将特征值λi代入方程式（5.5.55）可计算出θ和ψ。再将θ和ψ代入式（5.5.56），可得到连续梁按某i阶共振圆频率ωi下的支承弯矩比例值，再将这些支承弯矩的比例值代入式（5.5.53）和式（5.5.54）中，就可最终得到连续梁各跨上的振型曲线。

表5.5.4　多跨梁的自振圆频率比值

与单跨梁相同，连续梁振型函数φi（x）也具有正交性质。同理可证明，两个积分是对每跨在跨长l区间之内的积分之和。

附录F列出了2～10跨连续梁中前两个密集区处的振型曲线φi（x），这些曲线均为经过加权处理后的标准振型曲线，即满足

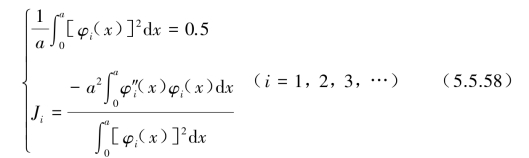
从多跨梁的振型分布曲线可清楚看出：

（1）每组密集区的第1个共振频率与振型与无密集区单跨梁的完全相同，例如5跨梁的（ω1，φ1），（ω6，φ6）与单跨梁的（ω1，φ1），（ω2，φ2）相同。

（2）在每个密集区中的振型的节点数仍按（i-1）规律递增。这里要注意：如在支承处振型曲线的斜率φ′i（x）=0（即曲率发生改变）时需认为是节点。

（3）只有在每个密集区第1个共振频率所对应的振型在每跨上最大振幅是完全相等的，如5跨梁中φ1和φ6、10跨梁中φ1与φ11的最大振幅均设定为1.00。