1)简支梁
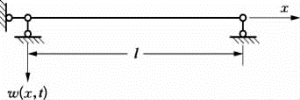
图5.5.2 简支支承的梁
简支梁的边界条件为两端支承的挠度和弯矩为零(见图5.5.2),即
φ(0)=φ′(0)=φ′(l)=φ″(l)=0
(5.5.14)
将式(5.5.14)代入式(5.5.12)第2式,得齐次特征方程为
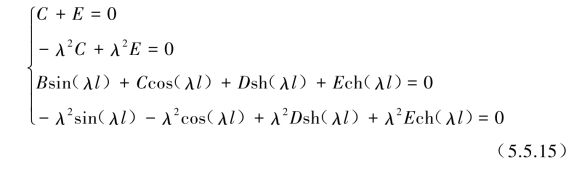
求得前两式C=E=0,后两式:
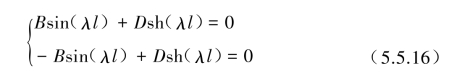
由于梁做自由振动,因此式(5.5.16)必须是方程的系数行列式为零,即
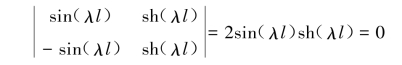
可得到
sin(λl)=0
求得
![]()
由式(5.5.13)可求得梁的固有圆频率ωi为
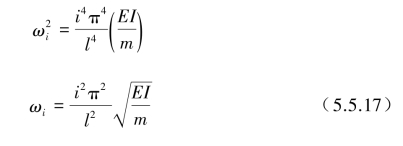
将λ=![]() 代入式(5.5.16)后得到对应ωi自由振动的振型φi为
代入式(5.5.16)后得到对应ωi自由振动的振型φi为
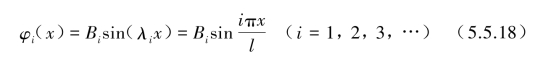
在梁上任一点x以及在任一时刻t的挠度wi(x,t)为
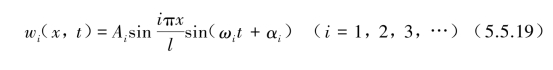
2)两端固支梁
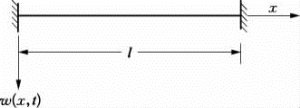
图5.5.3 两端固支梁
其固支梁的边界条件(见图5.5.3)为
φ(0)=φ′(0)=φ(l)=φ′(l)
(5.5.20)
由此得到齐次特征方程为(www.daowen.com)
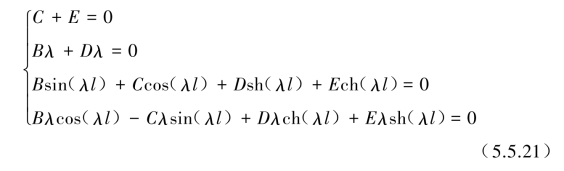
式(5.5.21)如存在非零的特征值解,其系数行列式为零,即
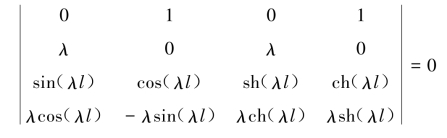
行列式展开后得特征方程为
cos(λl)·ch(λl)=1
(5.5.22)
求解式(5.5.22)可用数值解法,第一特征值为λl=4.730 0,后面各阶接近于cos(λl)=0的解,因此可近似表示为
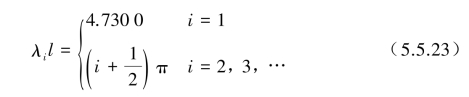
将λil代入式(5.5.21),求得B,C,D和E,然后代入式(5.5.12),得到两端固定梁的振型为
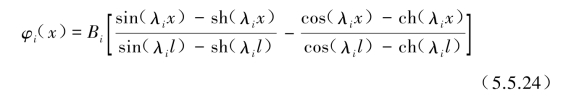
3)悬臂梁
悬臂梁的支承条件为一端固定,另一端自由(见图5.5.4)。
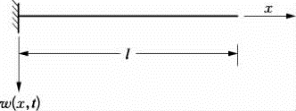
图5.5.4 悬臂梁
φ(0)=φ′(0)=φ″(l)=φ‴(l)=0
(5.5.25)
同理可得到特征值方程为
cos(λl)·ch(λl)=-1
(5.5.26)
近似解为
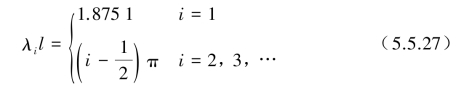
相应的振型为
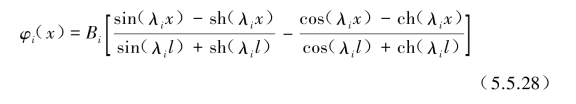
对于其他的边界条件,也可以得到固有频率与振型,这里不再赘述。6种不同边界条件下单跨梁的特征值λi、振型φi(x)及其φi的积分特性如表5.5.2所示。表中模态振型φi(x)为
φi(x)=Bsin(λix)+Ccos(λix)+Dsh(λix)+Ech(λix)
(5.5.29)
正则化的标准振型定义为
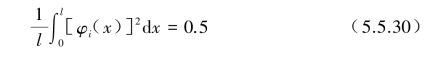
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








