设梁中性面的坐标为x轴，垂直于中性面的坐标为z轴。在梁的小挠度假设条件下，根据伯努利假设，当外载荷p作用在梁截面的对称平面内时，梁截面上距中性轴为z距离处的任何一点的水平位移u（x，t）与中性轴上的挠度w（x，t）的关系为

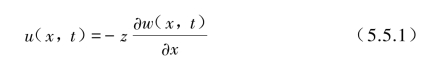
式中，表示梁弯曲的转角。图5.5.1中因z轴向下为正，所示转角为正条件下，离中性轴距离以下的z为正时，其对应的水平位移u则为负值，所以该式中需加负号来表示。

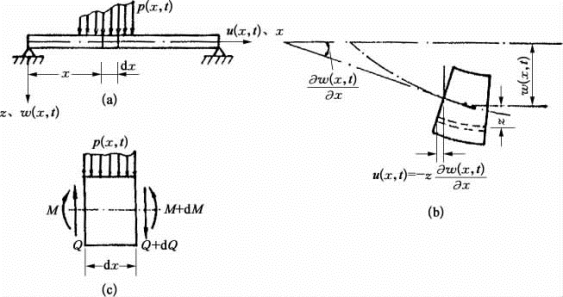
图5.5.1　变形协调关系

x方向的轴向应变εz（x，t）表示为

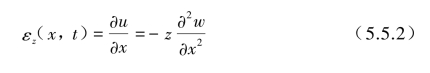
式中，表示在小位移w（x，t）条件下梁弯曲变形的曲率，也就是轴向应变εz与曲率变化成正比。根据材料胡克定律，梁截面上的法向正应力σz（x，t）为

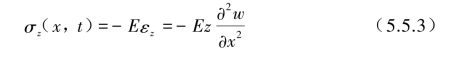
记梁截面上的轴向弯矩M（x，t）与σz关系为

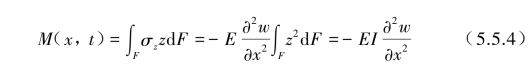(www.daowen.com)

式中，I=dF为梁截面上惯性矩，E为梁材料的弹性模量。

另外，根据梁微元dx截面上力系平衡条件［见图5.5.1（c）］得到

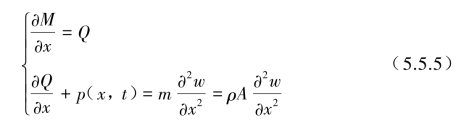
式中，p（x，t）为梁单位长度上的线分布载荷，Q为梁微元dx截面上的剪力，m为梁单位长度的质量，ρ为材料质量密度，m=ρA，A为梁截面的面积。

将上面两式合并后得

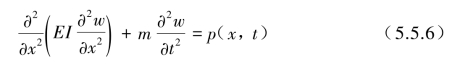
如等截面梁，惯性矩I为常数，因此有

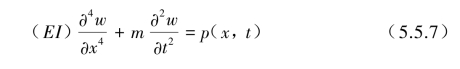
这是一个对坐标x的4阶，对时间t为二阶的偏微分方程。