当系统的基础上输入加速度时程，按式（5.4.3）与式（5.4.5）可求得模态激励力为

第j个模态力为fj=-。

假设系统是单个固定点或多个固定点输入相同的），则各整体坐标上的每个相对位移输出y均是相对于同一个输入的加速度值。因此式（5.4.17）中fj用来替代，可改写为

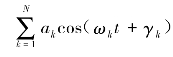地面加速度输入如按式（3.4.13）采用三角级数模型）=来模拟合成的人工地震波时，式（5.4.18）可表示为

式中，振型参与系数

再将式（5.4.19）代入式（5.4.11）积分项内的，并进行积分运算，可参考式（3.3.46）单自由度强迫振动解，则可得到各模态解qyj（t），和(www.daowen.com)

式中，Cj，φj，θj见式（5.4.12），其他

从模态主坐标qyj，谐振激励输出结果可清楚观察到均由3部分组成，第1部分是纯初始条件所确定的自由振动反应项，由于阻尼比ξj使该时程很迅速衰减。第2部分是伴随强迫振动反应项，它也随时间增长而迅速衰减。第3部分是真正的强迫振动反应项，其反应按激励圆频率ωk的谐振变化。

当系统结构的某个或几个固有圆频率ωj与基础激励谐振圆频率ωk相等时，该系统会发生共振，将ωk=ωj与对应ak值代入式（5.4.21）整理后得到的解为

从上式结果可明显看出，系统在共振时伴随强迫反应项和强迫反应项与基础输入的谐振幅值ak相比均放大了倍，将qyj，代入式（5.4.22）后得到整体位置i上的各个输出分量，因在各阶模态坐标中只是第j阶模态的反应发生共振，可近似将qyj，中不随阻尼比衰减的第3部分单独取出，则yi，可表示为