结构系统中的振动会消耗系统能量，这类能量损失的现象称为阻尼，结构系统能量损失的原因有：①结构阻尼，是由于材料内部摩擦或结构系统元件之间连接处的摩擦引起的；②黏性阻尼，是由于流体中运动所引起的；③库仑阻尼，是由一个物体在另一物体表面上的滑动摩擦运动引起的。在工程中与抗震设计分析中最常遇到的是上述第二种——黏性阻尼，多自由度振动系统的振动方程为

第2项表示黏性阻尼力与速度大小成正比。式中C为黏性阻尼矩阵，通常所使用的是比例黏性阻尼假设，即满足KM-1C=CM-1K假设条件。

瑞利阻尼又是一种特殊的比例黏性阻尼，假定质量矩阵M与刚度矩阵K线性组合与阻尼矩阵C成正比，它定义为

C=αM+βK

（5.3.2）

式中，α和β是比例系数（实常数），αM为质量阻尼矩阵，βK为刚度阻尼矩阵。

在应用质量和刚度阻尼时，整个系统的阻尼值由两个实常数α和β来确定，而α和β值则能用控制两个频率的阻尼比来确定。(www.daowen.com)

若ωr和ωs分别为阻尼比ξr和ξs所对应的模态圆频率，则

对于任何第j阶圆频率ωj所对应的阻尼比ξj可以将上式中α和β消去后算出：

式中，ξjm=　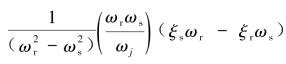为 质 量 阻 尼 引 起 的，ξjk为刚度阻尼所引起的。

式（5.3.4）表示阻尼比是质量阻尼与刚度阻尼的总和，当应用质量阻尼（α≠0，β=0）时，阻尼比将随频率的增加而减小。当应用刚度阻尼（α=0，β≠0）时，阻尼比将随频率的增加而增大。

在结构系统的地震分析时，由于运动方程通常是用相对于基础的位移来表示的，如果有两个主要频率的阻尼比已确定，则可采用质量和刚度阻尼，其他频率的阻尼比可借助式（5.3.4）算出。如果仅仅用刚度阻尼，对于主要频率ωr所确定的阻尼比是ξr，则采用β=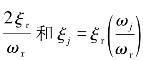）即可。

根据式（5.3.2），用无阻尼系统的实模态可以将比例阻尼矩阵C对角化，也就是说无阻尼系统下求得的实模态对这类比例阻尼具有正交性质。因此可以用实模态理论来分析具有比例阻尼的多自由系统的振动。5.2节中论述的关于无阻尼系统振动的实模态分析方法均可以直接用来分析具有比例系统的振动。