特征值ωj和特征向量｛φj｝是特征方程式（5.2.4）的解，因为每组｛φj｝也满足该方程，即为

将式（5.2.10）左乘｛φi｝T后得到

同理，对另一个特征值ωi和特征向量｛φi｝代入特征方程式（5.2.4），并左乘｛φj｝T得到

由于M和K矩阵的对称性，将式（5.2.12）两边转置，可得到

将式（5.2.11）与式（5.2.13）两边相减，得到

综上所述，ωi≠ωj条件下，则为

证明了模态关于质量矩阵M的正交性，同理也可得到

即是关于刚度矩阵K的正交性，式（5.2.15）和式（5.2.16）是对不同振动模态之间的特征值ωj不出现重根情况下成立，然而应用线性代数中的schur定理，仍可证明即使出现重根情况下，只要M是正定对称矩阵、K是半正定对称矩阵，同样可证明满足正交性模态。

当i=j时，可令：

式中，Mpj为第j阶模态质量，Kpj为第j阶模态刚度。

由式（5.2.12）或式（5.2.13）可得

该式的物理意义是对多自由度振动可以通过模态正则化后转化为在广义坐标系下成为独立的单自由度振动形式。

求得n个特征向量｛φj｝组成n×n的模态振型矩阵Φ为

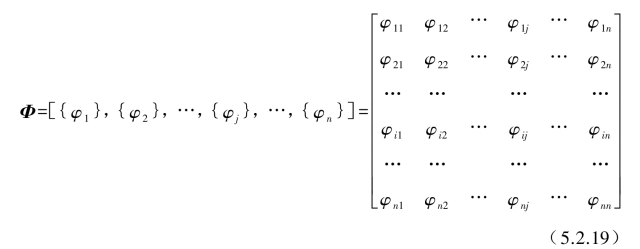
这里注意模态矩阵Φ中元素φij的含义，i代表在系统每个坐标上的位置，j代表第j阶固有频率下的振型。｛φj｝表示第j个固有频率下包含各坐标位置（i=1，2，…，n）上所对应振型的幅值大小。

根据质量矩阵M和刚度矩阵K的正交性，也可得到

式中，Mp=diag（Mpj）称为模态质量矩阵，Mpj称为第j个固有频率的模态质量值。同理可得到模态刚度矩阵Kp=diag（Kpj）为

这里注意由于模态是有正交特性且线性无关，因此模态矩阵Φ必定是满秩，即Φ也存在相应的逆阵。

由于Φ中各元素是相对长度关系，需要确定一个绝对长度来衡量，通常有两种方法来确定模态长度。

（1）式（5.2.15）在求解特征向量时，如令向量｛φj｝中的第1个分量定为φ1j=1，那么其他分量的大小就可根据φ1j来确定其比例值。

（2）如用模态质量来确定模态尺度，则称为质量归一化模态。

即令　对应的模态可记为ΦN，它与Φ的关系为

Mpj=1 （j=1，2，…，n）

（5.2.23）

将ΦN代入式（5.2.21）和（5.2.22）后相应变为模态质量和模态刚度归一化矩阵：

式中，I为单位矩阵，Ω=diag（）为对角元素矩阵，即

根据模态的正交性质，证明了各模态之间是线性无关的，也就是说，对一个n维（即n个自由度）多自由度系统可分解为n个独立的模态，构成n维向量空间正交组合群，那么向量y都可由这组正交组合群来表示，被称为模态坐标系，即

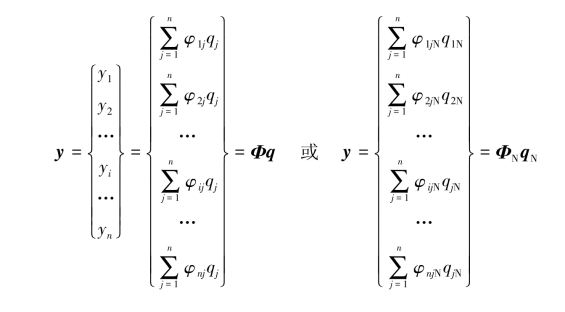
每个坐标点i上的输出位移为

式中，列向量q=｛q1，q2，…，qj，…，qn｝T称为模态坐标或主坐标列阵，列中元素qj称为系统的第j个模态坐标（或第j个主坐标），根据模态的正交性可得到

对于无阻尼下有n个自由度线性定常系统，动能T和势能U分别为

将式（5.2.29）分别代入式（5.2.31）后得到

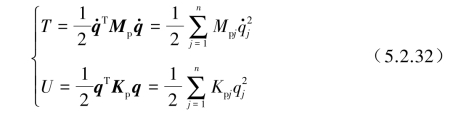
上式说明该线性系统的动能和势能等于各阶主振动各自的动能和势能之和。而且每一阶主振动的动能和势能之和在系统的自由振动中保持不变，即不同阶的主振动的能量互不交换，这是线性振动系统模态正交性最基本的物理意义。模态正交性还可以从另一角度理解为，若用模态坐标作为“广义坐标”来建立动力方程时，则系统在广义坐标下不存在惯性耦合与刚度耦合，也就是系统的模态质量矩阵和模态刚度矩阵是一个对角矩阵，因此该原理是模态叠加方法最基本的理论基础。

综合以上分析可知，对于多自由度系统固有特性的主要参数包括固有频率、模态振型、模态质量与刚度。

用式（5.2.30）中模态坐标来表征主振动时可以分解成n个独立模态坐标qi下的振动方程，即

［例1］ 图5.2.1所示为三自由度弹簧-质量系统，系统参数为m1=m3=2m，m2=m，k1=k4=3k，k2=k3=k，求该系统的固有圆频率与主振型。

图5.2.1　三自由度质量-弹簧系统

解：系统的质量和刚度矩阵分别为

系统的特征方程为

展开整理后得到特征固有频率方程式为

（k-mω2）（2k-mω2）（3k-mω2）=0

（5.2.37）（5.2.52）

解得3个固有圆频率为

将ω1代入式（5.2.33）得

设用第1种归一化振型方法，取φ11=1，代入式（5.2.39）后求得第1阶主振型为

同理将ω2和ω3分别代入式（5.2.36）后求得第2阶和第3阶主振型分别为

图5.2.2为各阶模态的振型图，从图上可清楚看出，对应第1阶固有频率ω1的模态的振型是各质点做同相位运动，振幅连线上没有节点。对应第2阶固有频率ω2的模态中，质点1和质点3做反相运动，而质点2处于平衡位置不动，各坐标的连线有一个零点，称为节点。对应第3阶固有频率ω3的模态中，质点1和质点3做同相运动，而质点2的相位与质点1和质点3的相位相反，则在坐标的连线上有两个节点。值得指出的是，系统的模态是固有的特性（包括固有频率与振型），与外部初始条件和激励均无关。

图5.2.2　各阶模态的振型(www.daowen.com)

模态质量为

模态刚度为

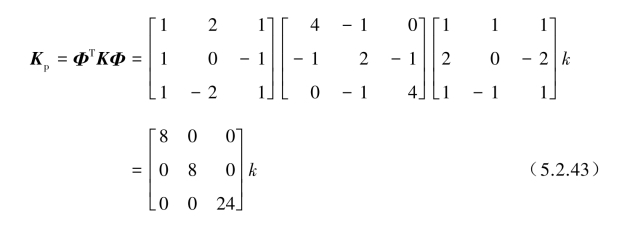
模态固有频率为

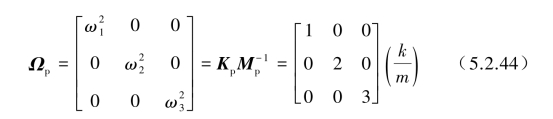
模态质量、模态刚度与模态固有频率分量的计算结果如表5.2.1所示。

表5.2.1　模态质量、模态刚度与模态固有频率结果

若用第2种质量归一化的模态求解方法，按式（5.2.24）可得到

由此可组合成质量归一化模态矩阵：

代入式（5.2.25）和式（5.2.26）可验证满足式（5.2.25）和式（5.2.26）。

［例2］ 图5.2.3（a）中，在两端简支梁上，有3个集中质量分布在等跨l/4处，设m1=m2=m，梁的弯曲刚度为EI，不计梁本身质量。试求梁弯曲振动式的固有频率与主振型。

图5.2.3　单位力F作用下的挠度

（1）求解简支梁在集中质量m1，m2和m3等3处的刚度矩阵时，可先采用柔度影响系数法建立3点上的柔度，再求逆后得到对应的刚度。

由材料力学公式可知，在x=a处有一单位力F=1作用在两端简支上，在距原点x处y方向的挠度δ计算式（见图5.2.4）为

式中，l为梁长，a，b为单位力作用点到梁两端的距离。

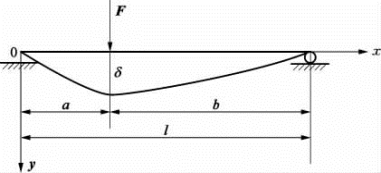
图5.2.4　简支梁在单位力作用下与位移δ的关系

当单位力F作用在x=l/4处质量m1点上时，其对应m1，m2和m3处的扰度设为δ11，δ21和δ31，将x=l/4，l/2和3l/4分别代入式（5.2.47）得

单位力F作用在x=l/2质量m2上时，同样可得到

单位力F作用在x=3l/4质量m3上时，同样可得到

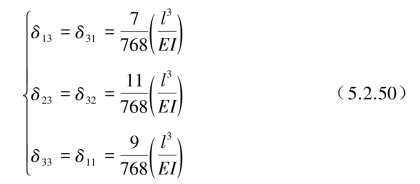
于是可以得到3×3的柔度矩阵：

柔度矩阵δ的含义是单位力F作用下的各点上的挠度y，之间的关系为

y=δF

式中

刚度矩阵K与柔度矩阵δ的关系为δ求逆，即K=δ-1，经矩阵求逆运算可得

（2）求解固有频率与主振型。

由自由振动方程式（5.2.1）左乘［δ］=K-1得

由K-1K=I得到

设α=，将式（5.2.51）的δ与M=m代入上式的振动方程后得

令主振型振动为式（5.2.2），将y=φsin（ωt+θ）代入式（5.2.55）得

令β=代入得到频率方程为

将行列式展开后得到方程：

β3-50β2+124β-56=（β-2）（β2-48β+28）=0（5.2.58）

由此可解得3个解为

β1=47.41，β2=2，β3=0.59

可得到3个固有圆频率ω为

当j=3，β3=0.59代入式（5.2.57）后，令φ31=1得

解得

同理i=2，β2=2；i=3，β3=0.59得到归一化主振型为

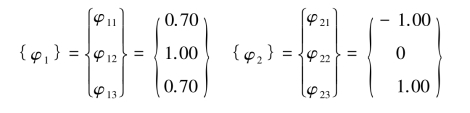
则归一化振型矩阵为

（3）求归一化质量的主振型。

模态质量为

求解各阶的可得

代入式（5.2.61）得到归一化质量的振型矩阵：

（4）验证。

归一化质量的模态质量是否为I

归一化质量的模态刚度是否与式（5.2.59）中相等。

证明该系统的尺寸归一化模态或质量归一化模态均正确。