方程式（5.1.1）求解无阻尼系统下的n个自由度自由振动问题可由下式列出：

y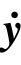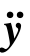，，为（n×1）位移、速度与加速度列阵。

自由振动微分方程式（5.2.1）的通解为

式中，

φ称为简谐振动振幅比值组成的n阶列向量，式（5.2.2）表示系统内各坐标在同时刻偏离平衡位置后，均在同一频率ω和同一相位θ条件下进行不同振幅的简谐振动。将式（5.2.2）代入式（5.2.1）后得到

变换成广义特征值代数形式的方程式，其中φ，ω2称为系统的特征向量和特征值（或通常称为固有频率）。将质量矩阵求逆，式（5.2.4）转化为

即

这就是线性系统中的特征值方程，式（5.2.5）是一个齐次线性代数方程组，其ω2非零解的条件是系数矩阵的行列式等于零，即

式（5.2.6）可以解得特征值ωj（j=1，2，…，n），从小到大排列为(www.daowen.com)

ω1＜ω2＜…　＜ωj＜…　＜ωn

（5.2.7）

ωj称系统第j阶无阻尼下的固有圆频率，ω1称为基频，一般情况下刚度矩阵K是半正定对称矩阵，det（K）≥0；质量矩阵M是正定对称矩阵，即det（M）＞0，因此系统的固有频率必定大于零或等于零。

将某个特征值ωj代入齐次代数方程式（5.2.6）后可得到与之相对应的特征向量｛φj｝，特征向量｛φj｝表达了各个坐标在以频率ωj做简谐振动时各个坐标幅值的相对大小，所以常常称为系统第j阶模态的固有振型，或简称为第j阶模态（或振型）。再将ωj和｛φj｝代入式（5.2.2）可得到

｛yj｝=aj｛φj｝sin（ωjt+θj） （j=1，2，…，n）

（5.2.8）

上式就是多自由度系统以ωj为固有频率以及｛φj｝为模态的第j阶主振动，系统的总反应就是各阶主模态振动的叠加，即

式中，aj和θj由初始条件来确定，θj在0～π之间变化。