【摘要】:图4.7.1子系统独立的抗震模型在抗震系统中的子系统和主系统不能满足4.4节的解耦条件时,如何将子系统从耦合主、子系统中分离出来,形成一个独立的单自由度系统进行分析,且需要满足何种条件等均是本节所要讨论的问题。该独立单自由度系统与子系统相同,为由m2,c2和k2所组成的模型,这时用从耦合模型中求得主系统的作为该模型的基础输入。
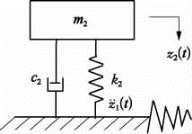
图4.7.1 子系统独立的抗震模型
在抗震系统中的子系统和主系统不能满足4.4节的解耦条件时,如何将子系统从耦合主、子系统中分离出来,形成一个独立的单自由度系统进行分析,且需要满足何种条件等均是本节所要讨论的问题。该独立单自由度系统与子系统相同,为由m2,c2和k2所组成的模型,这时用从耦合模型中求得主系统的![]() 作为该模型的基础输入(见图4.7.1)。
作为该模型的基础输入(见图4.7.1)。
单自由度振动方程为
![]()
设z2-z1=y2,代入式(4.7.1)后可整理为在相对坐标系统中的方程:
![]()
式中,ω2= ![]() 为子系统的固有圆频率,ξ2为子系统的阻尼比。
为子系统的固有圆频率,ξ2为子系统的阻尼比。
按式(4.6.16)相同表达,将基础输入![]() 由k个谐波组合的形式表示为
由k个谐波组合的形式表示为
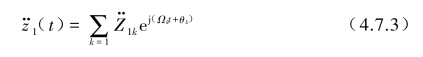
设在子系统上的相对位移反应为
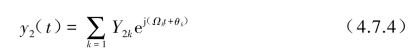
将式(4.7.3)和式(4.7.4)代入式(4.7.2)可求得输入![]() 幅值与输出幅值Y2k之间的关系为(www.daowen.com)
幅值与输出幅值Y2k之间的关系为(www.daowen.com)
![]()
由式(4.7.5)可得

再由式(4.7.1)可求得绝对加速度![]() 的幅值
的幅值![]() ,它与
,它与![]() 之间的关系为
之间的关系为
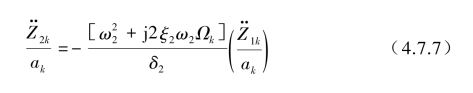
式中,δ2为
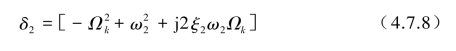
将δ2用幅值与相位关系表示为
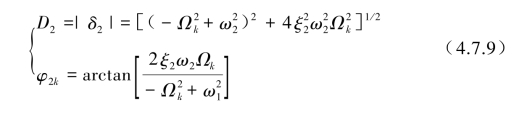
将式(4.7.6)和式(4.7.7)表示为
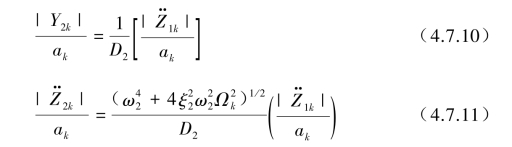
当已知输入加速度幅值![]() 后,从式(4.7.10)和式(4.7.11)可求得子系统相对位移y2的幅值|Y2k|和绝对加速度
后,从式(4.7.10)和式(4.7.11)可求得子系统相对位移y2的幅值|Y2k|和绝对加速度![]() 的幅值
的幅值![]() 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
有关核电厂设施抗震分析及应用的文章






