【摘要】:与4.2节采用相同的抗震系统,可简化为主系统和子系统组成的两个自由度振动系统,主系统由质量m1、刚度k1和阻尼c1组成,子系统由质量m2、刚度k2和阻尼c2组成。图4.6.1耦合抗震系统的两自由度模型由主系统m1上的绝对位移z1和子系统m2上的绝对位移z2所表示的振动方程为令相对位移:式中,y1是主系统相对于基础的相对位移,y2是子系统相对于主系统的相对位移。
与4.2节采用相同的抗震系统,可简化为主系统和子系统组成的两个自由度振动系统,主系统由质量m1、刚度k1和阻尼c1组成,子系统由质量m2、刚度k2和阻尼c2组成。基础地震输入的加速度时程为![]() (见图4.6.1)。
(见图4.6.1)。

图4.6.1 耦合抗震系统的两自由度模型
由主系统m1上的绝对位移z1和子系统m2上的绝对位移z2所表示的振动方程为

令相对位移:

式中,y1是主系统相对于基础的相对位移,y2是子系统相对于主系统的相对位移。代入式(4.6.1)得到一组由相对位移表示的耦合振动方程:

设
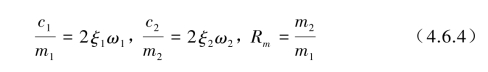 (https://www.daowen.com)
(https://www.daowen.com)
式中,ξ1,ξ2分别为主系统与子系统的阻尼比,将式(4.2.3)、式(4.2.4)、式(4.6.4)代入式(4.6.3)后可转化为以阻尼比ξ1,ξ2和ω1,ω2表示的振动方程:

设基础输入地震加速度时程![]() )由N个正弦谐波的组合式来模拟:
)由N个正弦谐波的组合式来模拟:
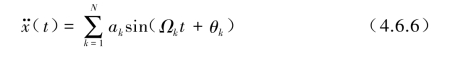
由于地震波是一类随时间变化的随机变量,因此其幅值ak可由![]() 对应的单边功率谱密度函数来表征:
对应的单边功率谱密度函数来表征:
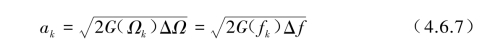
式中,G(Ωk)为![]() 在第k个圆频率Ωk上的单边目标功率谱密度函数,Δ?Ω是以Ωk(fk)为中心频率处的带宽,θk=0~2π内的随机数,k=1,2,…,N。
在第k个圆频率Ωk上的单边目标功率谱密度函数,Δ?Ω是以Ωk(fk)为中心频率处的带宽,θk=0~2π内的随机数,k=1,2,…,N。

式中,ΩH,ΩL为高、低端圆频率,N为高、低端圆频率的等分数。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章






