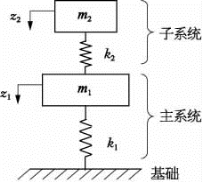
图4.2.1　主系统与子系统简化耦合模型

将抗震系统简化为主系统和子系统组成两个自由度振动系统，与基础相连的称为主系统，用质量m1和刚度k1表示；附在主系统上的称为子系统，用质量m2和刚度k2表示（见图4.2.1）。其无阻尼自由振动耦合方程为

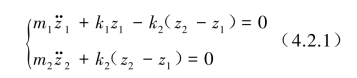
式中，z1和z2为质量m1和m2上的位移振动量。

设参数Rm和Rω（或Rf）为

式中，ω1和ω2分别为主系统和子系统独立时的自身固有圆频率。

将式（4.2.2）～式（4.2.4）代入式（4.2.1）后，可转化为如下的振动方程：

这是两个二阶线性常系数微分方程，它们的通解可用微分方程的两个特解按线性组合而成。式（4.2.5）为无外力作用、也不计阻尼的自由振动方程。若其特解为同步运动，即两个质点z1和z2各按不同的振幅Z1和Z2以相同的圆频率ω和相位α进行运动，则可设z1和z2为

如系统存在上式表述的特解，将式（4.2.6）代入式（4.2.5）后可得到一组与时间无关的恒等式，即sin（ωt+α）前的系数为零，整理后可得二阶矩阵方程，并能从中解出待定常数ω，Z1和Z2。

(www.daowen.com)

代数式（4.2.7）只有在方程系数行列式为零时，齐次代数方程才有不等于零的解，其系数行列式称为频率特征方程。

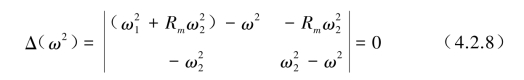
将式（4.2.8）展开后可得

这是ω2的二次方程式，它的两个根为

式中，

所以方程的根均为正实的重根，也就是说该系统只可能存在以为特征，另一个以为特征的两种形式的同步运动，为此这里可将称为该系统的主频率或固有圆频率。

对式（4.2.10）作根式运算可求得该系统耦合的固有圆频率更为简洁的解：

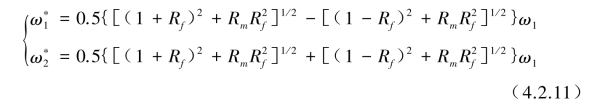
从式（4.2.11）可明显看出在系统主频率中的两个固有圆频率值有大小，在条件下，也可将称为基频，称为第二固有圆频率。