现以NRC发布的NUREG-0800-3.7.1《地震设计参数》中所规定的标准地面设计反应谱与对应的目标功率谱密度函数为例，该标准地面设计反应谱是以岩石为基础的水平分量，由图3.5.2（a）和表3.5.2给出，规定的最大水平地面加速度为1g（981 cm/s2），其适用的放大系数由5个频率控制点和5个不同阻尼比给出。所对应的目标功率谱密度函数由图3.5.2（b）和式（3.5.1）给出，表3.5.3是5个频率控制点上功率谱密度函数的计算值。

表3.5.2　标准地面水平加速度设计反应谱值Sa（f0，ξ）（cm/s2）

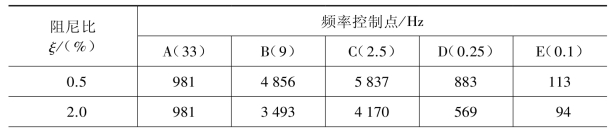
（续表）

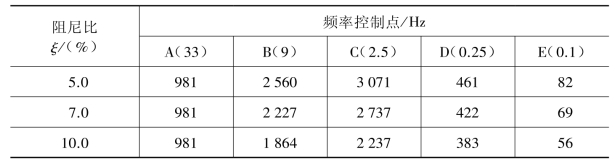
表3.5.3　目标加速度功率谱密度函数［（cm/s2）2/Hz］

从式（3.5.59）和式（3.5.60）可还原出由表征的求解超越阈值置信度Prob（λ，-λ）的表达式：

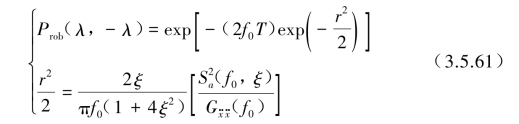
式（3.5.46）修正为

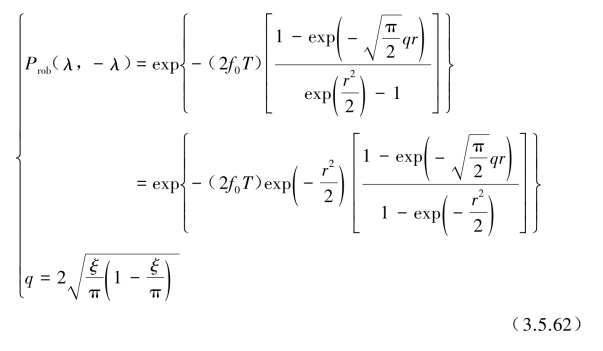
输入标准水平加速度设计反应谱）、目标功率谱密度函数、5个频率控制点f0和不同阻尼比ξ由表3.5.2和表3.5.3的值分别代入式（3.5.61）和式（3.5.62），这里设强震的时间为T=20 s，其Prob随f0和ξ关系结果列于表3.5.4和表3.5.5，其曲线如图3.5.7所示。

表3.5.4　按原始公式（3.5.61）计算的超越阈值概率置信度Prob(www.daowen.com)

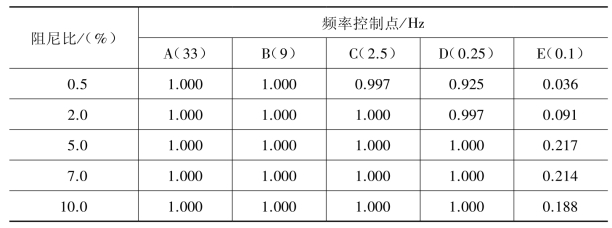
表3.5.5　按改进公式（3.5.62）计算的超越阈值概率置信度Prob

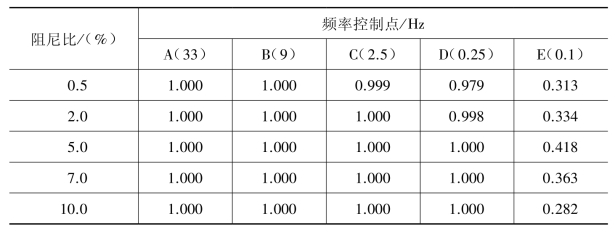
从计算结果表3.5.4、表3.5.5可清楚看出：

（1）按原始公式（3.5.61）计算置信度Prob时，随阻尼比ξ值的增加以及控制频率点f0的增加，其置信度也相应提高。

（2）按原始公式（3.5.61）计算置信度Prob时，控制点低频0.1 Hz处的Prob值最低，而按改进后公式（3.5.62）计算Prob值时，则可提高置信度Prob值，特别在0.5%和2%的小阻尼比ξ下可更明显地提高Prob。这主要由于公式中计入了功率谱参数q的作用，即形状扩展系数q随阻尼比ξ减小而同步在减少，因此在处理很低阻尼比时引入了马尔科夫假定，是为了处理反应中所产生连续穿越阈值诱发性，特别是针对较低控制频率0.1 Hz时更为明显。

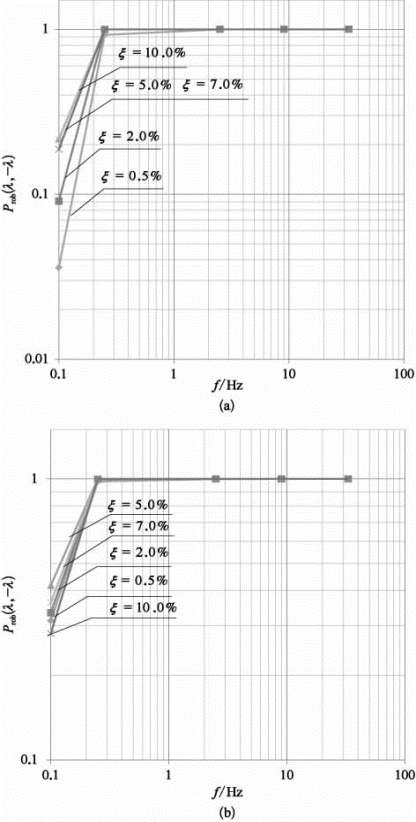
图3.5.7　超越阈值概率置信度Prob

（a）原始公式（3.5.61）计算；（b）改进公式（3.5.62）计算

（3）按原始公式（3.5.61），假设为平稳高斯随机过程，不考虑各控制频率f0和阻尼比ξ进入强震阶段的非平稳效应，在极小阻尼比ξ和极小固有频率f0下，进入平稳状态的强震区域时间会更长，因此造成在低阻尼比ξ和低控制频率f0下的Prob置信度偏低。尽管如此，对绝大多数Prob的置信度还是接近100%，说明该标准地面加速度设计反应谱Sa所对应的地面

输入加速度的目标功率谱密度函数还是确切的。

（4）采用假设的平稳高斯随机过程的公式（3.5.61）和局部采用式（3.5.62）作改进是可行的。我国有关地震学方面学者胡聿贤、赵凤新、张郁山等进行过详细的研究，并将该实用的公式推荐给国家标准《核电厂抗震设计》（GB50267-20XX）应用。