1）无穿阈次数问题的解析

2.4.2节已阐述随机过程的概率密度函数p（x）的应用问题，如某x（t）假设为平均为零的平稳随机过程，则其高斯分布形式的概率密度函数p（x）和对应的概率分布函数P（x）可表示为

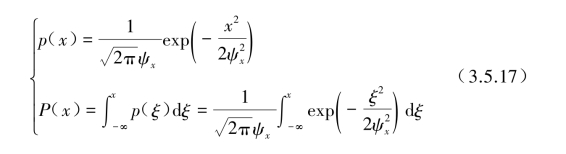
式中，ψx为x（t）的均方根值，即ψx=ψ［x（t）］。

典型标准化p（x）和P（x）可将式（3.5.17）中参数设为

标准化正态概率密度和分布函数可表示为

图3.5.4是标准化正态概率密度p（z）和分布函数P（z）与z的关系曲线，它表示了不同归一化幅值z=所对应的概率密度和概率分布值，也就是说在x（t）随机时程曲线上出现幅值大小与概率密度值的大小形成一定的统计定量值。

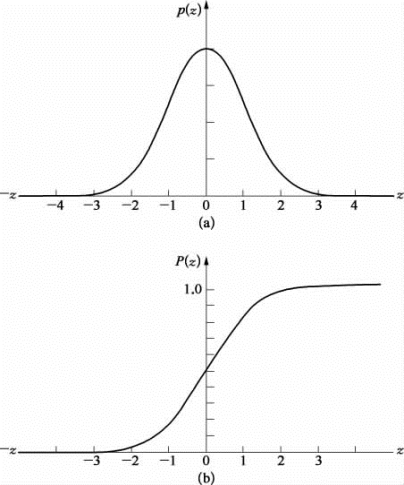
图3.5.4　标准化概率密度与分布函数

（a）概率密度函数；（b）概率分布函数

在以后的应用中，采用指定概率P（z）=1-α时的z值称为阈值zα，即式（3.5.19）可表示为

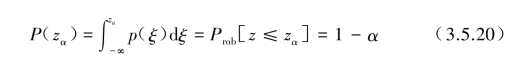
或

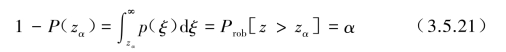
也就是说，α是表示幅值在整个时域中超出指定阈值zα时的概率，定义为［1-P（zα）］=Prob［z＞zα］。反之定义为P（zα）=Prob［z≤zα］为不超出指定阈值zα时的概率。

通常将阈值zα用百分比表示更为直观。对平稳随机过程x（t）可通过相关的幅值分析程序（如雨流法）得出类似于图3.5.4的正态分布概率密度函数p（z）和对应的分布函数P（z）。

2）有穿阈次数问题的解析

实际上针对一个随机过程x（t）的时程曲线上给定一个x=λ阈值时，如除波的峰值处外，均出现在一个正半波或负半波上各出现两个交点的情况（见图3.5.5），那么称为“有穿阈次数问题”，对穿阈次数的统计值是计算动态问题可靠性的一个重要的基础。设随机过程x（t）的初始值x（0）=0，在时间间隔［0，T］内，x=λ的穿阈总次数为n（λ，T），对应的期望值为N（λ，T）=E［n（λ，T）］。为此，图3.5.5中针对x=λ与x（t）穿过阈值λ处再构造一个从0～1过程的y（t），及其导数y·（t）函数，设

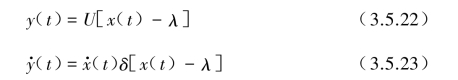
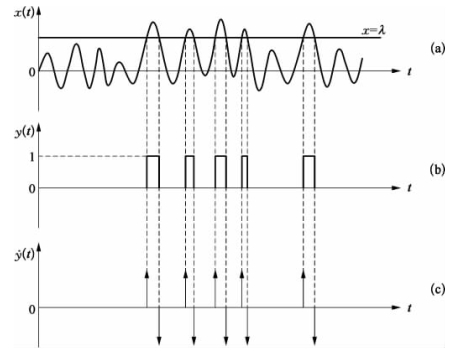
图3.5.5　x（t），y（t）和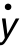t）函数的图形

式中，U（t）为单位阶跃函数；δ（t）为狄拉克单位脉冲函数，是U（t）的斜率。若用数学方法可表示为

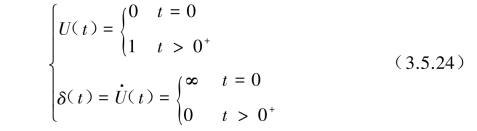
从图3.5.5可知，由样本函数所示的图形是由单位脉冲所组成的，一个向上的脉冲对应于x（t）一次以正斜率穿越阈值λ，一个向下的脉冲对应于x（t）一次以负斜率穿越阈值λ，包含正负在内的脉冲总次数为n（λ，T），将式（3.5.23）在时域T内积分后可得

对应穿阈次数的期望值可利用x（t）和x·（t）的共概率密度p（x，x·，t）来计算。

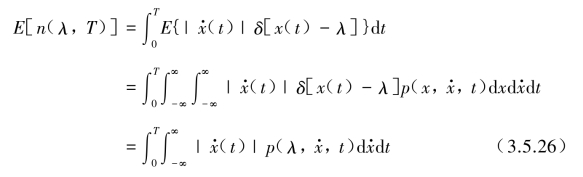
单位时间穿越阈次数的期望值也称为期望穿越阈值率，设为νλ（t）

若x（t）为平稳随机过程，穿越阈期望值不按时间t发生变化，则式（3.5.27）变为

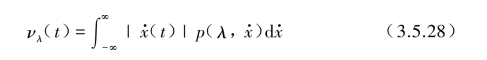
若将穿越阈值λ以正斜率或负斜率来计算期望次数时，只需将式（3.5.26）分别对的正、负区域积分即可，得到下面两组。

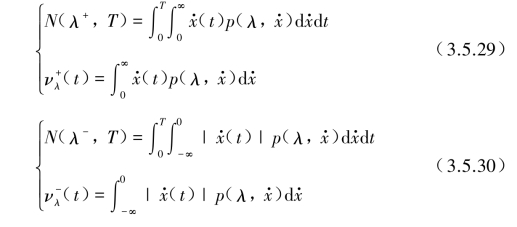
对平稳随机过程，（pλ，）是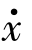的偶函数，一个正斜率的穿越阈λ+必然伴随一个负斜率穿越阈值λ-，从而可得

对于均值为零的平稳高斯随机过程的情况，x（t）和可认为是相互独立的，其概率密度函数为

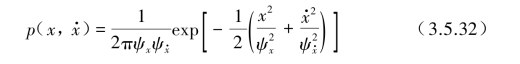
将式（3.5.32）代入式（3.5.29）和式（3.5.30）中的后积分得

若利用附录I中关于x（t）功率谱密度函数G（ω）的谱参数定义，则

将式（3.5.34）中λ0和ω2代入式（3.5.33）可得到总期望穿越阈值率νλ为

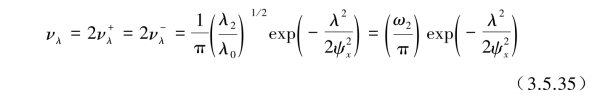
当λ=0时，期望穿越阈值率ν0达到最大值为

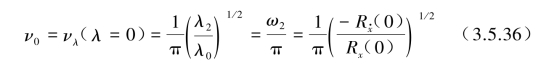
式中，Rx（τ）和为x（t）和的自相关函数。

式（3.5.36）也可用正斜率和λ=0穿越阈值率来表示：(www.daowen.com)

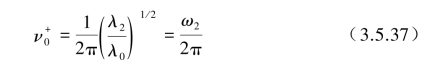
该式表征对于一个窄带平稳随机过程的期望频率ωe（或fe），其穿越率fe达到最大，即

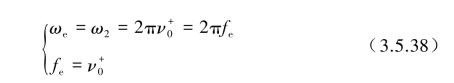
3）穿越阈值概率的分布函数

上面针对x（t）随机过程获得穿越阈率νλ值，那么还需要获得在［0，T］时间内的穿阈λ值的分布函数，因此可设定将式（3.5.25）中正负在内脉冲总数n（λ，T）视为随机泊松过程，可分别表示为

式中，由式（3.5.29）和式（3.5.30）给出。

当考虑到x（t）的穿越阈值1次也不超出上下界限λ+和λ-时，

可认为对应分布概率为

考虑到x（t）和，t）对于原点的对称性，所以可得到类似式（3.5.31）的共概率密度p（x，关系，代入式（3.5.41）后得到

（1）对平稳随机过程，）与时间无关，式（3.5.42）可变为

将用式（3.5.35）代入式（3.5.43）可给出1次也不超出阈值λ的概率：

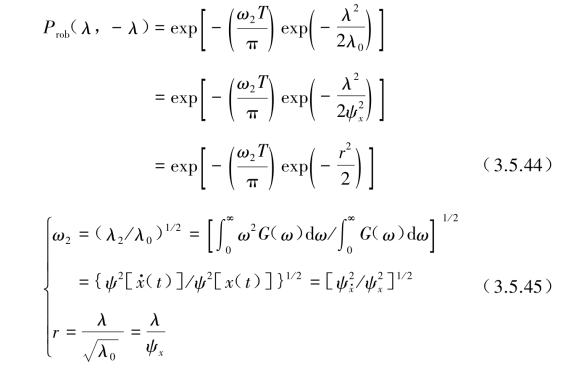
式中，r为穿越阈值λ与x（t）的标准均方根ψx之比，T为随机过程x（t）间隔的总时间，λ0，λ2和ω2为x（t）的功率谱密度函数G（ω）在附录I中定义的谱参数。式（3.5.44）通常认为与精确解存在一定差别，但其结果偏于安全，所以常得到应用。

Vanmarcrke提出了改进的表达式：

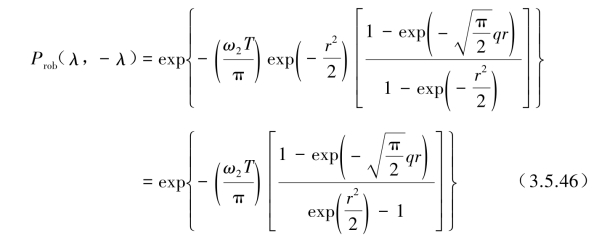
式中，q=为谱参数。

式（3.5.46）应用了谱参数q加以修正，可看出当q为较小值时的窄频带随机过程，或者低超越阈值λ（r为小值）时，与式（3.5.44）比较，其结果得到了改善。

（2）对非平稳随机过程）与时间有关，根据式（3.5.42）得

在非平稳条件下，式（3.5.35）中ω2和（或λ0）均用时间t的函数给出，t）则表示为

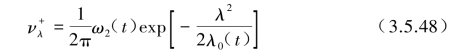
将上式代入式（3.5.47）后得

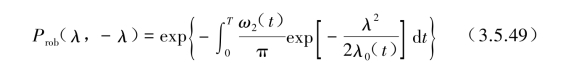
利用式（3.5.34）的谱参数ω2和λ0代入上式后可得到超越阈值λ的概率Prob（λ，-λ）值。Corotis等改进了式（3.5.49）得到与式（3.5.46）相对应的计算式。不同的是其中谱参数与比值均为时间t的函数，即

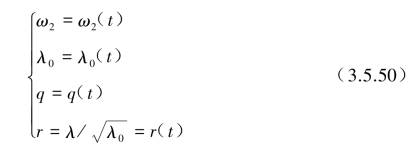
（3）Corotis等应用平稳随机过程的式（3.5.44）与改进式（3.5.46）以及非平稳随机过程的式（3.5.49），对阻尼比ξ=0.01，0.1的单自由度体系反应作了计算，其结果分别如图3.5.6（a）和（b）所示。

图3.5.6中曲线含义分别说明如下：

PS——由式（3.5.44）计算，为平稳高斯过程x（t）的分布概率Prob与ω0t的关系。

MS——由式（3.5.46）计算，为平稳高斯过程x（t）改善PS的分布概率Prob与ω0t的关系。

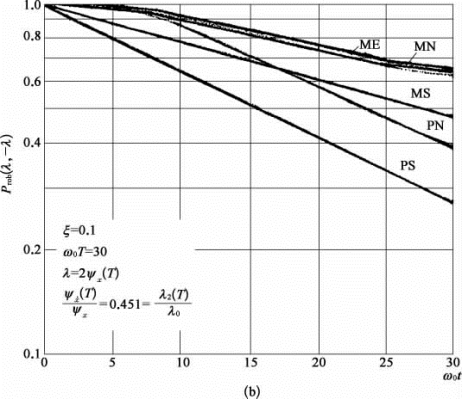
图3.5.6　不同阻尼比下的穿越阈值Prob（λ，-λ）的概率

（a）ξ=0.01；（b）ξ=0.1

PN——由式（3.5.49）计算，为非平稳高斯过程x（t）的分布概率Prob与ω0t的关系。

ME——由式（3.5.50）计算，为非平稳高斯过程x（t）的改善PS［式（3.5.46）］分布概率Prob与ω0t的关系。

MN——同MS［式（3.5.46）］计算，但其中将反应均方根ψx作为时间t的变化函数考虑。

从计算结果可清楚看出：

（i）在小阻尼情况下，PS（平稳）给出偏于安全的概率Prob值。这是由于假定为平稳过程，而实际上其反应是从静止状态逐步转移到平稳过程，所以阻尼比较大时，离精确解更接近以及偏离值更小，从而使置信度提高。

（ii）PN与PS相比，由于标准均方根ψx（t）作为时间函数给出，但与其他曲线相比，仍然给出偏于安全的数值。

（iii）MS曲线是对PS曲线的改进，虽比PS曲线提高了计算偏差和置信度，但由于没有考虑非平稳过程，显示出在时间前阶段尚未能得到正确结果。

（iv）MN虽对MS作了改进，但由于q值与时间无关的定值，小阻尼下的初始状态可认为仍给不出正确结果。

（v）综上，ME已克服其他计算公式中的缺陷，可认为给出最接近正确的解。

（vi）也可将穿越阈值λ（或-λ）的概率分布函数Prob（λ，-λ）认为是未超越阈值（λ，-λ）的置信度，（1-Prob）为超越阈值（λ，-λ）的置信度。