3.4.1节对地面地震波的随机过程模拟作了描述，但还需进一步了解地震波的特性，特别在抗震设计时要知道的重要特性有以下3点：

（1）持续时间及其他的包络函数。

（2）最大加速度或最大速度。

（3）频率成分。

（1）在上述三者中，地震运动的持续时间可根据大量的实际测量记录来量化。图3.5.3所示地震波加速度时程的包络曲线g（t）。包络曲线可分为3个阶段，0～Tb之间为起始阶段，是用二次曲线描述；Tb～Tc之间为强震阶段，可用水平直线描述；Tc～Td之间为衰减阶段，是用指数衰减曲线描述。表达式如式（3.5.6）所示。

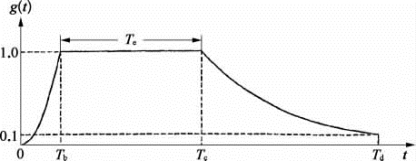
图3.5.3　地震波加速度时程的包络曲线

图3.5.3中，Te=Tc-Tb，是指主震运动的时间，称为有效持续时间或强震持续时间。Td，Tb，Tc和Te是大致可与震级M相关的一个统计值，下述的统计值仅作参考。

表3.5.1列出了Tb/Td，Tc/Td与震级M之间的大致关系。

表3.5.1　时间比关系

图3.4.1是典型的地震加速度时程曲线，图3.5.3是它的包络曲线，它归属于常用的非平稳随机过程模型，可描述为

式中，是平均值为0的平稳高斯过程，一般表示在图3.5.3中第2阶段的强震部分。

若g（t）不为常数条件，则）是表示随时间过程g（t）变化，相应的非平稳性函数，其常规的性质如下：

（i）的平均值可表示为

（ii）的自相关函数可表示为(www.daowen.com)

取t1=t2=t则为的均方值ψ2［］为

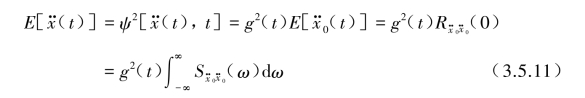
（iii）的自功率谱密度函数可表示为

（2）地震波的第2和第3个特性的量化远没有第1个持续时间那么简单，一般需要经大量的地震波测量数据作统计加以描述，最大加速度或最大速度一般指地面基底为准则定出，而基底指纵波波速（即地震波）约为1.3±0.4 km/s范围内的基岩和固结土层。

基底上最大加速度与震级M和震中距R的函数关系的估计参考公式为

式中，amax为最大加速度，d为震源深度（km）。

lg d=0.353M-1.435

（3.5.14）

基底上最大速度与震级M和震中距R的函数关系估计参考公式为

lg vmax=0.61M-RlgX-Q

（3.5.15）

式中，vmax为最大速度，X为震源距。

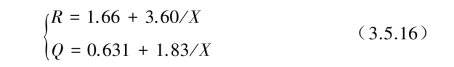
（3）第3个特性是指由频率控制点组成的地面反应谱。3.3.4节和3.3.5节作了详细阐述。另外输入地震波可由频率控制点组成的加速度功率谱密度（PSD）函数表征其频率特征，例如图3.5.2（b）所示地面加速度输入的目标G（f）是与图3.5.2（a）所示的地面设计反应谱Sa（f0，ξ）相对应的。两个图中所指频率特征的区别在于，设计反应谱横坐标是用单自由系统固有频率特征的ω0（或f0）来表征，目标功率谱密度函数横坐标是用输入地面加速度固有频率成分特征的ω（或f）来表征，这两者不能相混淆。

附录I专门讨论了平稳随机过程与非平稳过程的“谱参数”的求解方法与性质，这些参数对下面讨论地震反应谱与功率谱密度函数之间的关系以及核电厂抗震设计分析中结构安全度定量评价是十分有用的。