由图3.5.1可知，对一个地震动时间历程输入后，可用时域和频域两种方法获得其相对位移，相对速度和绝对加速度的反应。

第一种通过时域路径可得到式（3.3.57）Sd，Sv和Sa的反应表达式。

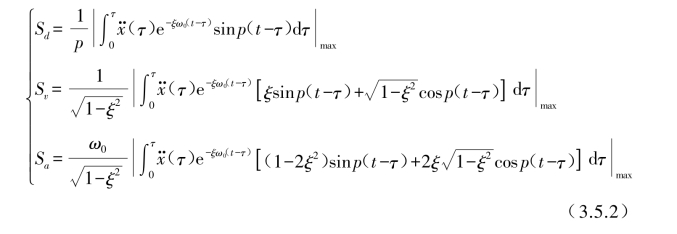
式中，Sd，Sv和Sa为相对基础位移y、相对基础速度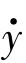和绝对加速度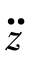的最大反应谱，它们是（ω0，ξ）的函数，ω0和ξ为单振子的固有圆频率和阻尼比。

附录B专门阐述了反应谱精确计算的理论文本及验证。

对于图3.5.1中第二种通过随机振动频域路径可得到与式（3.5.2）相对应的反应式（3.4.54）和式（3.4.55）。

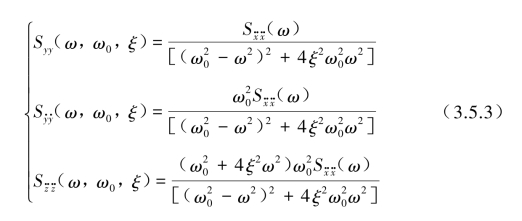
式中，为输入的加速度双边功率谱密度函数；(ω，ω0，ξ）为输出相对位移y（t）、相对速度和绝对加速度的双边功率谱密度函数；ω为频率成分；ω0和ξ为振子的固有圆频率和阻尼比。(www.daowen.com)

为了得到反应的相对位移，相对速度和绝对加速度幅值，可将式（3.5.3）代入下式后对ω全程（-∞，∞）积分得到各自的均方值。

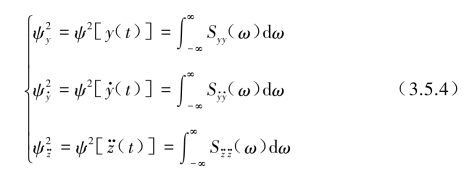
如假设输入是各态历经平稳随机过程的宽频带噪声，则输出可近似表示对应于振子ω0，ξ为变量时的均方值。

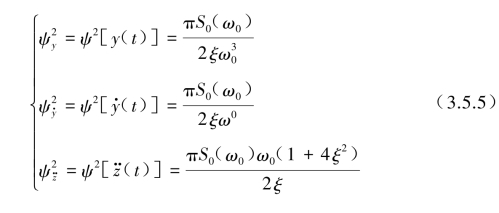
式中，S0（ω0）为输入的功率谱密度函数在ω0处的值，注意这里的S0（ω0）是双边功率谱密度函数；ψ2［y（t）］、ψ2［］、ψ2［］分别为反应y（t），的均方值，均是变量ω0和ξ的函数。

从式（3.5.5）可清楚看出，如果改变不同的ω0和ξ值，同样可以画出“位移、速度和加速度均方根值随ω0和ξ变化的3个反应谱”，如用式（3.5.5）与式（3.5.2）中Sd，Sv和Sa比较可看出，式（3.5.2）得到的反应谱幅值是反应的最大绝对值，而式（3.5.5）得出的反应谱幅值则是反应的均方根值，它们之间存在一个均方根值与峰值的变换关系问题，即如何将均方根值正确地换算到峰值以及两者之间是否存在着某种特殊的联系，则是问题的关键。