当单自由度振动系统在基础上输入一个位移x（t）时（见图3.4.4），由式（3.3.6）、式（3.3.7）可求得相对位移反应y（t）与绝对加速度z··（t）反应为

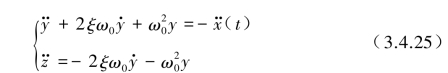
式中，ω0=为无阻尼下的圆频率；ξ为阻尼比，ξ=为临界阻尼系数，cc=2mω0=2

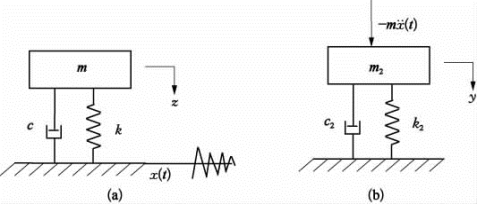
图3.4.4　单自由系统上基础输入

（a）原系统；（b）等效系统

当基础输入函数为一个随机变量函数时，则其输出（yt）和（zt）也应是一个随机变量函数。假设为一个各态历经平稳的随机过程，则的自相关函数与y（t）和z（t）的互相关函数也是一个各态历经平稳的随机过程，可定义为

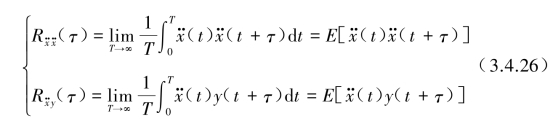
而输出信号y（t）与z（t）的自相关函数则可定义为

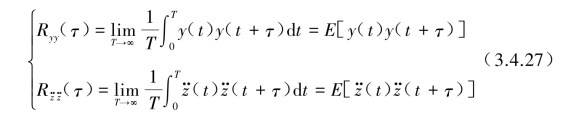
从式（3.4.26）、式（3.4.27）可清楚看出，虽然是一个随时间变化的随机变量，但经过相关统计后与则是转化为近似确定性函数的统计值，则可利用二次统计方法将式（3.4.25）转化为一个新的相关函数表示的微分方程式。首先对式（3.4.25）第1式分别左乘x··（t+τ）与y（t+τ）后取统计均方值，并利用相关函数微分性质：

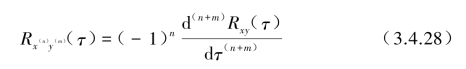
式中，（n），（m）表示对时间t的微分阶数，即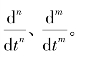

由此经运算可得到一组二阶线性微分式：

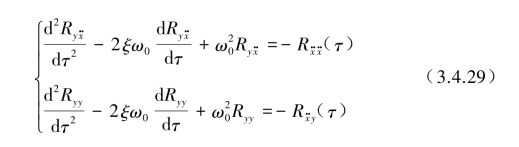
再利用相关函数性质：

代入式（3.4.29）后得到关于输出为的线性微分方程组：

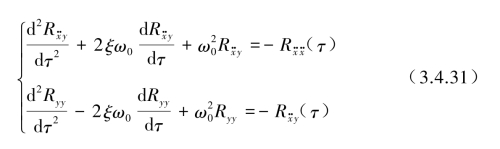
对式（3.4.25）第2式以同样方法分别左乘y（t+τ）和z··（t+τ）得到输出为的关系方程式：

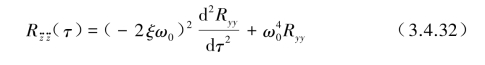
式（3.4.31）与式（3.4.32）是表征一个平稳各态历经随机过程的线性系统，图3.4.5展示了与式（3.4.31）与式（3.4.32）在时域τ中的输入输出线性过程关系。

图3.4.5　时域τ中输入输出关系

对于式（3.4.31）与式（3.4.32）可以应用常规的确定性振动模型系统进行求解，仍然与3.3.2节分别求解其通解和特解的方法相同。

1）自由振动解

将式（3.4.31）转化齐次方程：

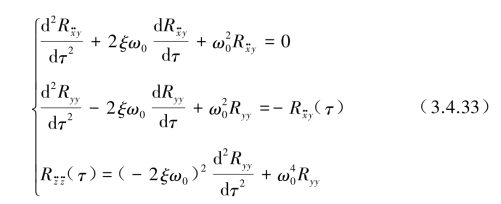
齐次方程初始τ=0时条件为

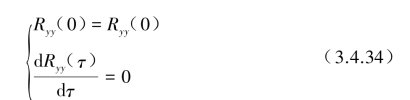
如将式（3.4.33）合并表示为的四阶线性微分方程：

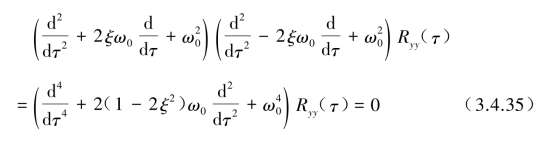
设Ryy（τ）=eSτ代入式（3.4.35）得到齐次微分方程的特征值方程式为

其方程的4个根为

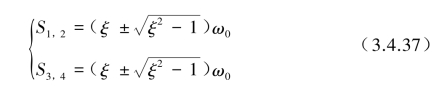
如振动系统的阻尼比ξ＜1时，则特征值为

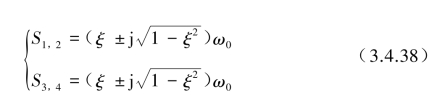
方程齐次解为

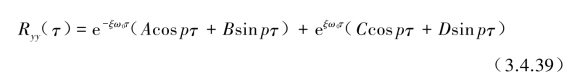
式中，p=A，B，C，D为积分常数。

由于振动齐次解随时间τ增大而衰减至零，因此解Ryy（τ）中C=D=0。

积分常数A，B由初始条件式（3.4.34）求得

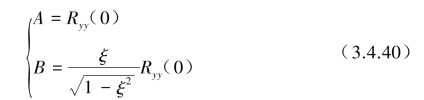
代入式（3.4.39）后得Ryy（τ）的解为

将Ryy（τ）与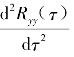代入式（3.4.32）整理后得

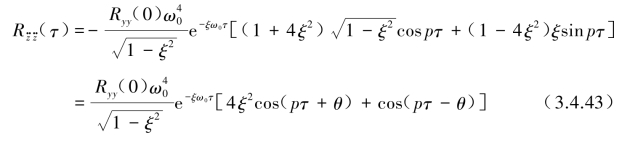
当τ=0时的即为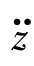（t）的均方值：

相位角θ见式（3.3.18）所示。

由平稳各态历经随机过程齐次方程式（3.4.33）的自由振动解式（3.4.41）～式（3.4.43）可以得到如下结论。

（1）对于平稳各态历经随机线性系统经过参数均方处理后所建立的相关函数线性振动方程可表征为确定性输入输出线性方程。

（2）其相对位移y（t）的自相关函数Ryy（τ）与绝对加速度z··（t）的自相关函数的自由振动之解由于阻尼比ξ随相关时间τ而迅速衰减。

2）强迫振动解

从前面已求得方程式（3.4.41）、式（3.4.43）的通解可知随相关时间τ的增加，由于阻尼比ξ而使其相关函数解Ryy（τ）和）衰减更快，对方程强迫振动的解在达到一定的时间后初始条件已影响不大。为此更简易的方法是对方程式（3.4.29）应用傅里叶变换方法求解方程的特解。即设的关

系对方程式（3.4.29）进行如下的傅里叶变换。与功率谱密度

得到新的频率域ω上以功率谱密度表征的方程式，然后进行傅里叶变换得到方程的特解。

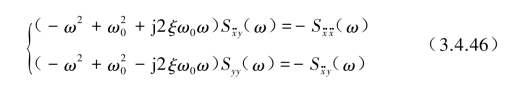
设

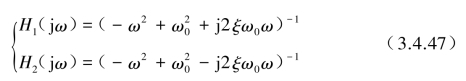
式（3.4.46）可改写为

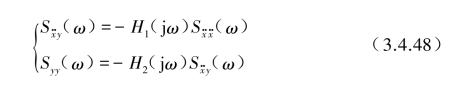
由傅里叶变换的性质可知，H1（jω）和H2（jω）对应反变换关系分别为

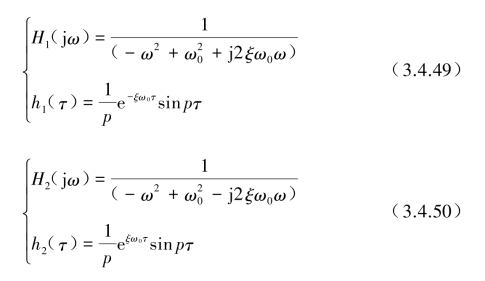
这里通常称H1（jω）与H2（jω）为线性系统中的传递函数，而对应时域τ的反变换函数h1（τ）和h2（τ）称为脉冲响应函数，也就是当线性系统输入为一个脉冲函数δ（τ）时，在频率域和对应时域上的响应为式（3.4.49）和式（3.4.50）。那么，特解和Ryy（τ）分别为

将代入式（3.4.51）第2式中），进行变量调整运算可得到Ryy（τ）的特解表达式为

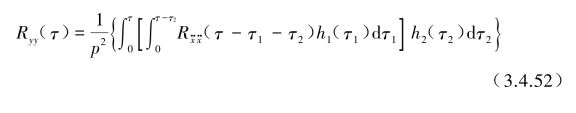
其另一表达为(www.daowen.com)

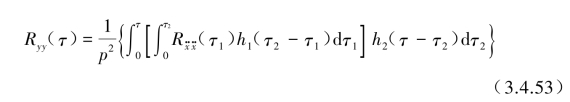
方程特解式（3.4.51）和式（3.4.52）中时域τ定义为｛0，∞｝区间内适用。

由式（3.4.48）可求得相对位移y（t）的功率谱密度函数Syy（ω）与输入自功率谱密度函数之间的关系为

由方程式（3.4.32）作傅里叶变换得到之间的关系为

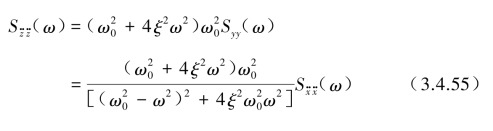
将Syy（ω）和进行傅里叶变换可得到自相关函数Ryy（τ）和：

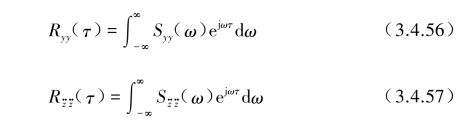
［例1］ 当基础地震波输入近似假设为白噪声时，其功率谱密度函数为一常数S0［单位为（m/s2）2/Hz］。则自相关函数变换为一个单位脉冲函数：

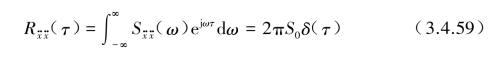
将式（3.4.59）中的代入式（3.4.54）～式（3.4.57）后进入积分运算，并可利用下列两个关系式：

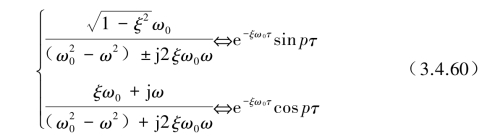
为此可得到相对位移y（t）的Ryy（τ）、相对速度的以及它们之间的互相关函数表达式：

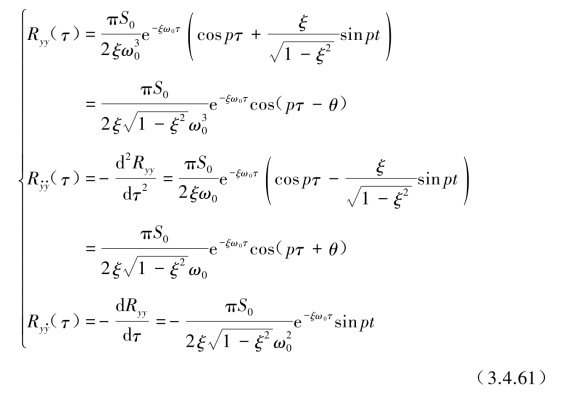
同样的方法，可得到绝对加速度z··（t）的相关函数为

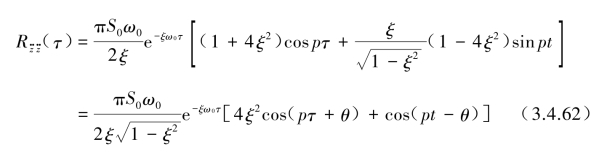
式（3.4.61）与式（3.4.62）中的相关时间τ的区间均为τ≥0范围，式中θ为

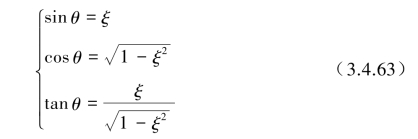
由此，当τ=0代入可得到相对位移y（t）、相对速度与绝对加速度z··（t）的均方值ψ2［y（t）］，ψ2［］与ψ2［）］为

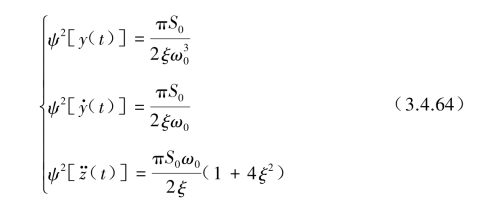
对于阻尼比ξ非常小时，Ryy（τ）与之间的关系可近似表示为

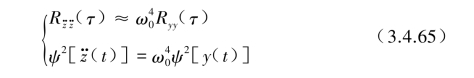
［例2］ 当基础地震波输入近似假设频率带宽为ω1≤ω≤ω2范围内的白噪声时，可表示为

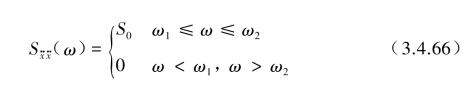
则式（3.4.54）和式（3.4.55）中输出功率谱密度）为

设频率比无量纲u=ω/ω0代入式（3.4.67）：

式中，积分下限u1=ω1/ω0，上限u2=ω2/ω0。

设

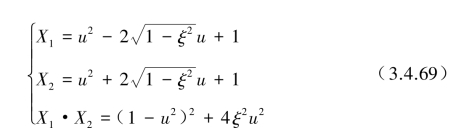
代入式（3.4.68）后可表示为

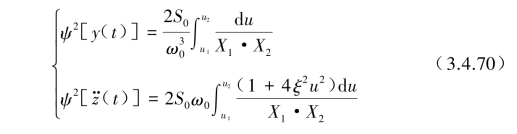
对于式（3.4.70）积分式分别作X1和X2的分解，可得到如下分解式：

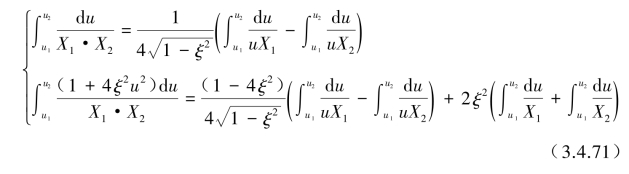
这样，可以根据X1和X2的二次函数式进行积分后整理得到相对位移y（t）和绝对加速度z··（t）的均方值。

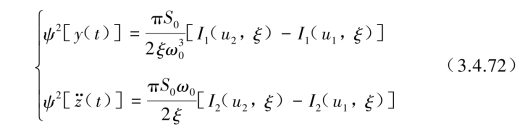
式中的因子为

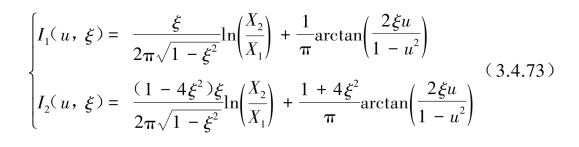
图3.4.6描述了I1（u，ξ）因子与u的关系曲线，当阻尼比ξ很小时，可认为I2≈I1，则

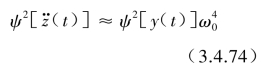
另外，当u1=0，u2→∞时（即ω1=0，ω2→∞），分别代入式（3.4.72）后得到

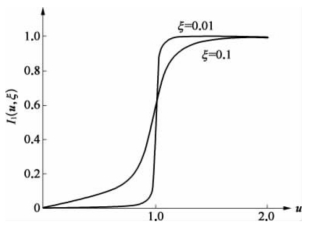
图3.4.6　I1（u1，ξ）曲线

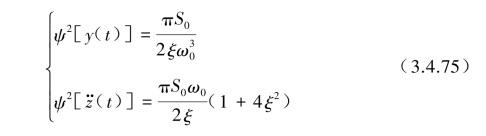
这时其均方值与白噪声激励相当。从图3.4.6的I1（u1，ξ）曲线也可以看出当系统的固有频率ω0落在ω1与ω2之间时，那么I1因子接近1。从方差的角度而言，带宽的白噪声也可近似等于理想白噪声来处理。实际中许多设备常见的属于小阻尼特征下，则系统的传递函数曲线在ω=±ω0附近出现陡峰（见图3.4.7），即使如果输入功率谱密度不是白噪声（即称为有色噪声），当的频带比|H（jω）|2的频宽（如峰值带宽，即半功率点输出带宽2ξω0）宽得多，即小阻尼条件时，输入功率谱密度函数就可以用共振点ω=ω0（u=1）处的来替代，而输出的均方值可近似表示为

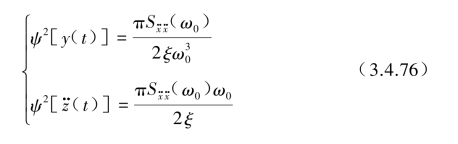
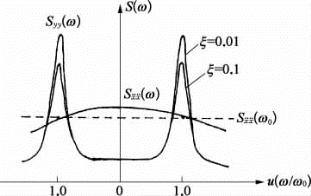
图3.4.7　振动输入Sxx（ω）与反应Sy（ω0）功率谱密度曲线函数比较

对于输出相对速度t）的均方值可由输出功率谱密度积分后求得，由关系式=ω2Syy（ω）代入ψ2［］得

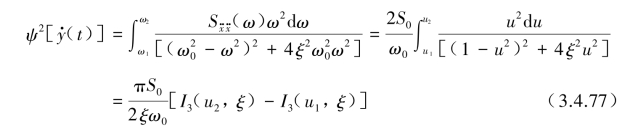
式中，

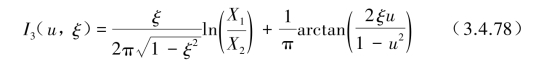
图3.4.8描述了I3（u，ξ）因子与u的关系曲线，同理当u1=0，u2→∞（即ω1=0，ω2→∞）时，则得到与式（3.4.64）相同的均方值ψ2［］。

对于式（3.4.31）的特解可以将式（3.4.54）和式（3.4.55）分别得到的Syy（ω）和作傅里叶反变换后变成为自相关函数Ryy（τ）和。或者直接由式（3.4.52）按积分方法求得输出自相关函数Ryy（τ）或。

图3.4.8　I3（u1，ξ）曲线

当输入是白噪声S0时，可以看出该特解Ryy（τ）和与通解式（3.4.41）～式（3.4.43）表达式完全一致，这里只要将式中系数Ryy（0）改为y（t）输出的均方值

Ryy（0）=ψ2［y（t）］=即可，因此这里不再一一列出其特解。

对于方程的特解可以清楚地得到如下结论：

（1）当基础输入地震波

假设为各态历经平稳随机信号时，其反应（yt）与t）也是各态历经平稳随机信号仍成立。

由于功率谱密度函数与相关函数之间相互匹配成为傅里叶变换配对，为此可作出如图3.4.9所示的输入输出联系图。

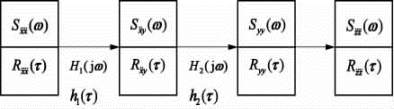
图3.4.9　频域ω与时域τ中的输入输出关系

（2）基础输入地震波假设为白噪声后，其反应y（t）与的均方值与阻尼比ξ成反比，阻尼比ξ愈小，其反应愈大。

（3）如结构物固有频率ω0落在激励带宽白噪声的带宽频率范围（ω1，ω2）内时，则其反应功率谱密度Syy（ω）或上存在ω=ω0的谱峰，其大小也与阻尼比ξ成反比，这时求解反应均方值表式中的输入功率谱密度值可近似用（见图3.4.7）。