3.3.3节已阐述单自由度振动系统基础加速度输入作用下的结构的反应y2，的求解方法和结果，从式（3.3.39）、式（3.3.40）或式（3.3.46）可清楚地看出其反应是时间t、系统固有圆频率ω0（或固有周期T0）和阻尼比ξ的函数，它们随时间不断地变化。从核电厂构筑物、系统和部件（SSC）抗震设计和分析的角度出发，与求解反应时间变化曲线相比，从工程角度更希望知道的是反应的最大值，即反应的位移、速度和加速度的最大值是多少。设地震时单质点系产生的最大相对位移反应、最大相对速度反应和最大绝对加速度反应分别为Sd，Sv和Sa，将式（3.3.31）～式（3.3.33）中忽略伴随强迫振动随时间变化衰减的影响后可变换为

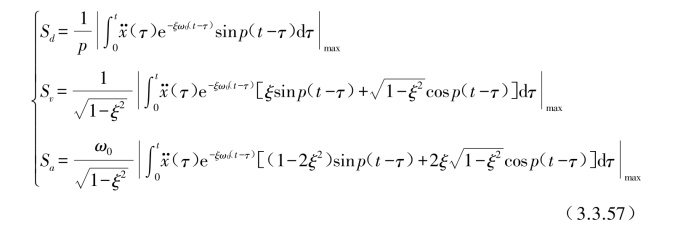
当输入基础的地震加速度时间历程给定后，式（3.3.57）是ω0（f0或T0）和ξ的函数，即为Sd（ξ，T0）、Sv（ξ，T0）和Sa（ξ，T0）。

以阻尼比ξ为参数，这些函数Sd，Sv和Sa对无阻尼比固有周期T0（或固有频率f0）所描绘的图分别称为相对位移反应谱、相对速度反应谱和绝对加速度反应谱，总称为地震反应谱，或分别简称为位移反应谱、速度反应谱、加速度反应谱，总称为反应谱。

地震反应谱在ASME BPVC第Ⅲ卷，第1册附录N-1110中定义为一族理想线性、单自由度、有阻尼振子上的最大反应（加速度、速度或位移）曲线，反映了当振子在其支承处有特定的振动运动输入时，其反应与固有频率（或周期）发生的函数关系。

地震反应谱生成的基本概念可用图3.3.5来说明。

步骤1：如图3.3.5（a）所示的同一平台台面上安放一系列阻尼比均为ξ2，而固有圆频率ω0（或周期T0）各异的谐振振子，也可理解为一组质量-阻尼-刚度单自由度振动系统。在图中仅列出3个振子，3个不同周期中T01较短、T02中等和T03较长。它们同在某个地震加速度）激励输入的台面上。

步骤2：台面上各质点随着台面的运动而出现按不同频率在摇动，显示了对输入加速度的反应，所测得的绝对加速度反应可得到图3.3.5（b）中的时程曲线记录。

T01较短，其反应振得也较快；T03较长，其反应振得也较慢。其振子反应振幅的变化与输入加速度密切相关，但是振子反应的周期几乎与输入无关，仅与振子本身固有特性有关。

(www.daowen.com)

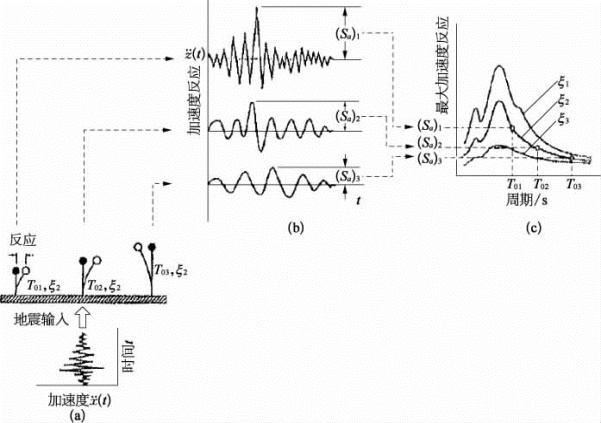
图3.3.5　地震反应谱图解

（a）阻尼比一定，由不同周期T0组成的单质点振动系统；（b）反应波形；（c）反应谱

步骤3：找出这些加速度时程z··（t）上的最大峰值［见图3.3.5（b）］，分别设为（Sa）1，（Sa）2和（Sa）3。在图3.3.5（c）中横坐标上周期T01，T02和T03处对应纵坐标上以（Sa）1，（Sa）2和（Sa）3对应表示3个点。

步骤4：当图3.3.5（a）的基础上并列了众多个周期差别很小的一组单质点系时，就可以得到像图3.3.5（c）上一条最大加速度Sa的曲线，而这组单质点振子的阻尼比均为ξ2，若改变ξ值后，再重复上述同样步骤后就可得一簇对应于不同阻尼比ξ下的地震最大反应曲线。图3.3.5（c）所示曲线簇就称为输入地震加速度反应谱。

图3.3.5中采用的质点振动反应是加速度，对应可得到加速度、位移y（t），则按上述同样步骤1～步骤4运算，分别可得到速度反应谱和位移反应谱。

图3.3.6分别列出了某地地震波对应于阻尼比=1%，5%和10%的加速度反应谱、速度反应谱和位移反应谱。反应谱。若采用的质点振动反应是速度

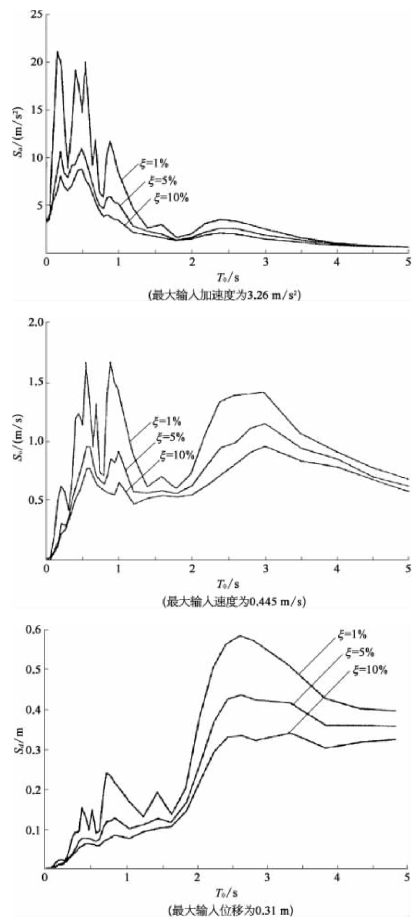
图3.3.6　地震反应谱采用周期表示

本书附录B详细列出了求解加速度反应谱的时间差分格式，用每步时间间隔h=tn+1-tn计算下步tn+1时的位移、速度和加速度时均要计及tn时刻的位移Yn、速度作为初始条件，因必须要用到式（3.3.33）中的总解，y=y1+y2，y=以及式（3.3.33）中的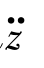表达式或者采用式（3.3.34）和式（3.3.35）。