设基础输入加速度时程为简谐激励时，其加速度为

式中，a为谐波振幅，ω为谐波激励频率。

将式（3.3.36）代入单自由度强迫振动的解式（3.3.31）得到强迫项的积分式特解为

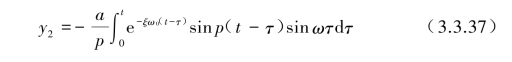
将积分式中t-τ=t1后该积分可变为

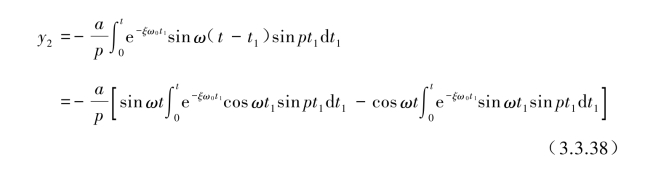
经过推导得到特解y2和为

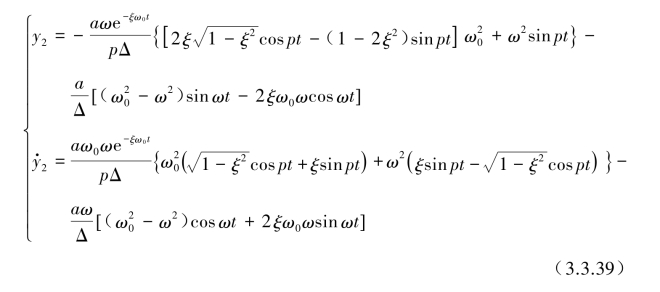
绝对加速度的特解为

式中，符号Δ和p为

从y2，的结果表达式中可看出两个重要的性质：

（1）当初始t=0代入式（3.3.39）和式（3.3.40）后，得到

说明振动系统的特解y2，与初始条件无关，仅由式（3.3.11）和式（3.3.12）的通解y1和来确定积分常数即可，即

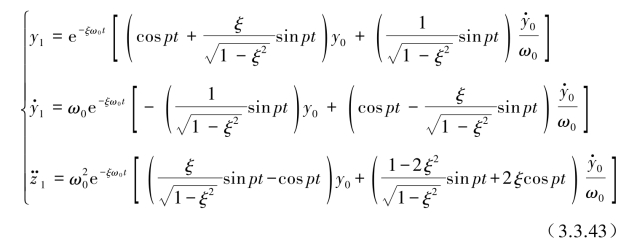
（2）对强迫振动的全解为y=y1+y2。第1部分y1称为自由振动的解，仅与初始条件y0和有关，并以共振频率p随时间做振荡的衰减运动。第2部分为y2表达式（3.3.39）中右边第1项，它是与强迫振动激励频率ω有关，但仍以共振频率p随时间做振荡的衰减运动，通常称为“伴随强迫项的自由振动”。第3部分为y2表达式（3.3.39）右边第2项，该项不同于前面两个部分，它以外部激励频率ω做周期性变化的无衰减运动，所以它称为“全程性强迫振动”，而当第1和第2两部分振动按e-ξω0t衰减后，只剩下第3部分无衰减的强迫运动。

图3.3.3为位移y（t）曲线，其中虚线是按ω频率做周期运动的强迫振动；而实线是初始时共振频率为p的衰减运动与强迫振动的叠加，它经过一个短时间后，其瞬态的自由振动和伴随振动由于阻尼原因而消失，剩下稳态的周期性强迫运动。

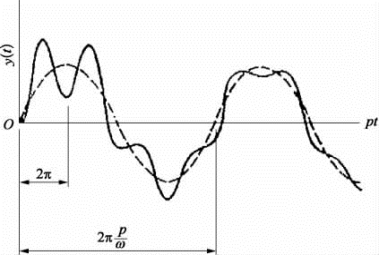
图3.3.3　强迫振动初始阶段

对于式（3.3.43）的自由振动解y1，也可用更简洁的方式来表达：

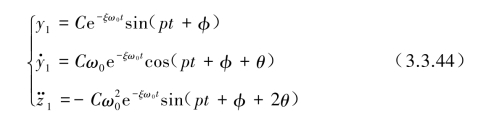
式中，

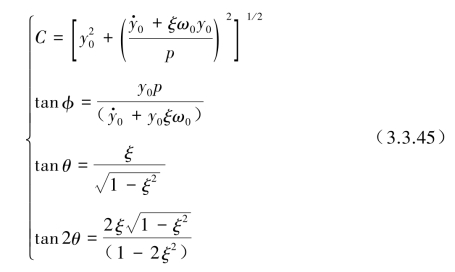
对于式（3.3.39）和式（3.3.40）的强迫振动解y2也可用更简洁的方式来表达：

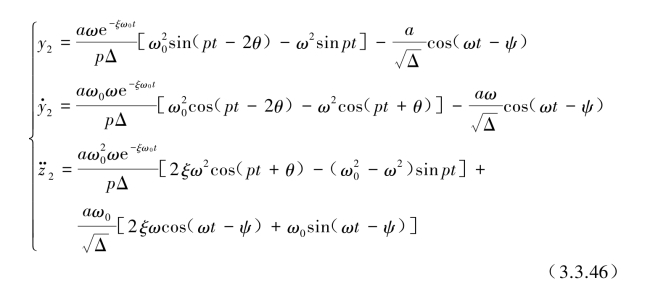(www.daowen.com)

式中，

其余符号同式（3.3.45）和式（3.3.41）。

当基础激励加速度的频率ω与系统固有频率ω0相等时，该系统会发生共振，将ω=ω0代入式（3.3.39）和式（3.3.40）后得到

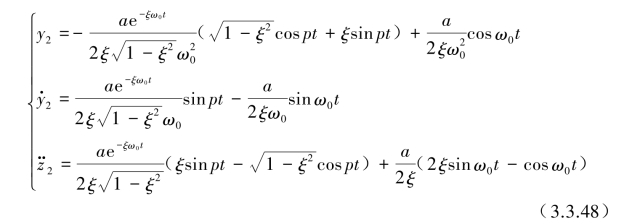
也可用简洁方式表示：

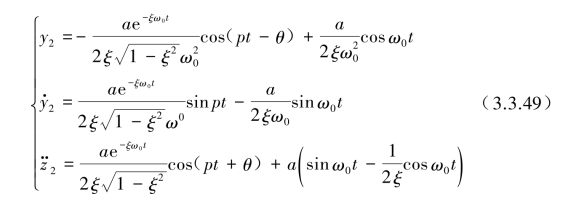
从上式可明显发现，系统在共振时其伴随强迫项或强迫项的振动反应幅值相当于基础输入幅值均放大了倍，也就是说振动系统的阻尼比ξ愈小，其在共振频率处的幅值反应愈大。

如果基础输入加速度时程为周期性函数，则可以将期T内展开成傅里叶级数形式。在周

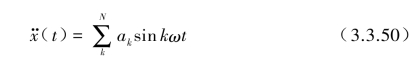
其傅氏系

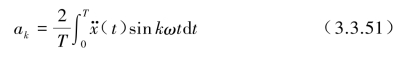
数该式表示了基础激励加速度可以分解为N个（kω）圆频率的谐波输入，而单自由度振动系统反应的解可以把幅值ak和激励圆频率ωk=kω代入式（3.3.39）和式（3.3.40）的解后，对k=1，2，…，N的线性叠加即可。

［例］ 若输入基础加速度是一个幅值为A、圆频率为ω的矩形波（见图3.3.4），求解强迫振动的解。

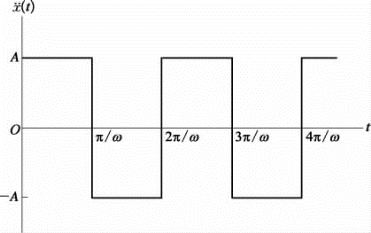
图3.3.4　矩形波的输入加速度

矩形波展开为傅里叶级数可得到

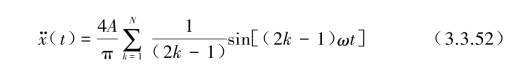
按照式（3.3.51）可得到ak为

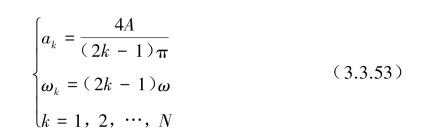
代入式（3.3.46）整理后得特解y2，为

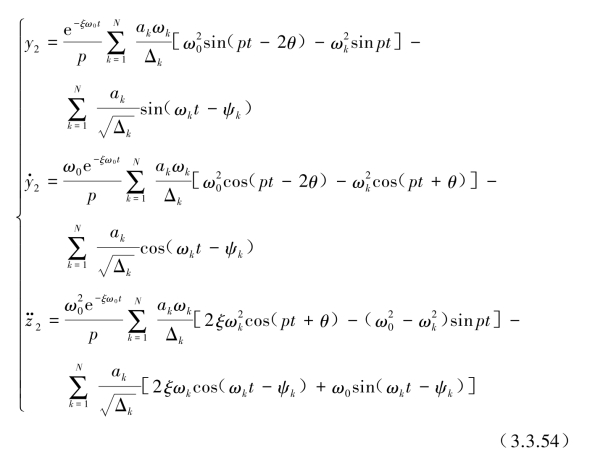
式中，

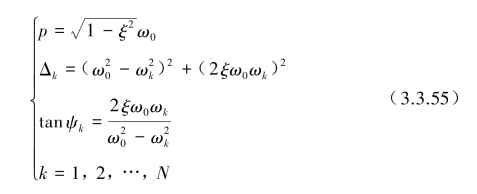
当外部激励频率ωk=（2k-1）ω与系统共振频率ω0相等时，该系统发生共振。如忽略初期瞬态自由振动和伴随强迫振动的影响，仅考虑稳定阶段后的稳态强迫振动，这时式（3.3.54）中仅考虑第二项强迫振动。用ωk=ω0代入得到稳态强迫振动的最大幅值的近似值。

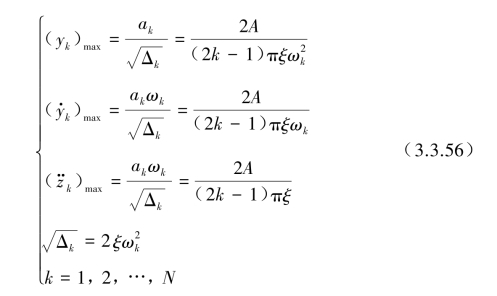
上式近似最大幅值结果可作为求解地震反应谱时的一个十分有用的参考，以实证所编制的地震反应谱求解器或专用程序的计算结果是否可信，并可求其不确定性的误差有多大。