当ξ<1时,即小阻尼条件下,很容易求解方程(3.2.3)的两个根为
![]()
式中,p=![]() 为系统的共振频率。
为系统的共振频率。
式(3.2.2)位移和速度的解为
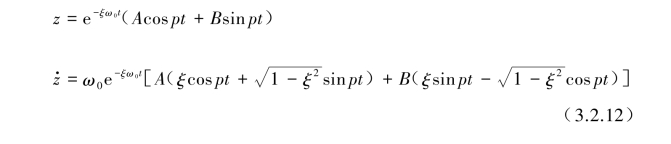
A,B为积分常数,可由初始条件t=0时z=z0和![]() 代入式(3.2.12)后求得。
代入式(3.2.12)后求得。

则通解为
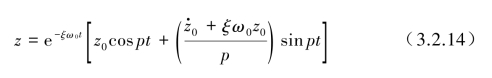
通解式(3.2.14)通常有下列两种表示形式。
(1)由初始条件直接表示。
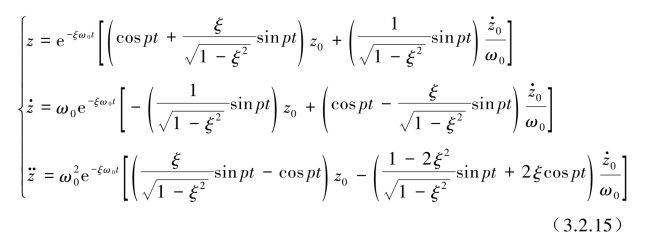
(2)由更简洁的方法表示。
在式(3.2.12)中常数A和B由幅值C和相位角φ来替代。
设幅值 C=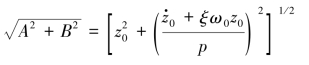
相位 sin φ=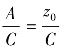
cos φ=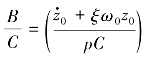
代入式(3.2.14)得到z的简易表达式为
![]()
由此对式(3.2.16)求导后可求得速度为
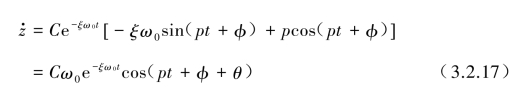
设:
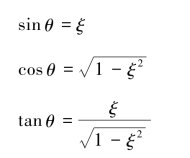
加速度可由式(3.2.2)直接求得
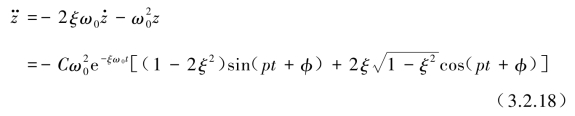
设:
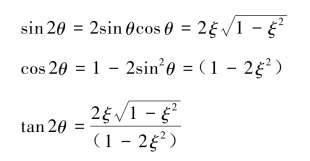
代入式(3.2.18)整理得
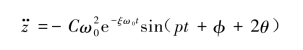 (https://www.daowen.com)
(https://www.daowen.com)
式中,p=![]()
将位移、速度与加速度汇总得
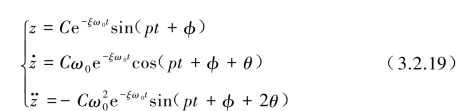
从以上两种不同表达形式的解可清楚地看出,该系统的运动属于小阻尼作用下的振动,其振动频率p=![]() 小于系统无阻尼下的固有频率ω0。对于何种初始条件下,系统的位移、速度与加速度幅值随时间变化均按指数形式衰减,最终趋向零位(见图3.2.4)。
小于系统无阻尼下的固有频率ω0。对于何种初始条件下,系统的位移、速度与加速度幅值随时间变化均按指数形式衰减,最终趋向零位(见图3.2.4)。
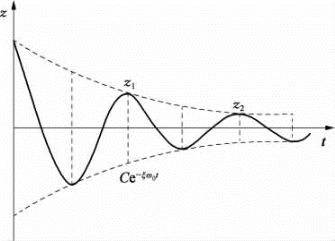
图3.2.4 小阻尼下的对数衰减曲线
从图3.2.4可明显观察到,在对数衰减曲线上任意相邻两次振动的振幅z1和z2之比为
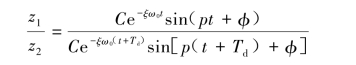
由于正弦函数满足周期性质,故上式简化为
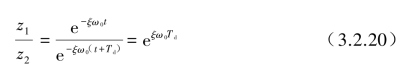
该比值取e为底的对数后称为“对数衰减率”,即
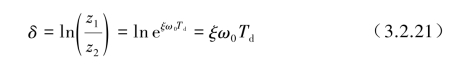
式中,衰减振动的周期Td为
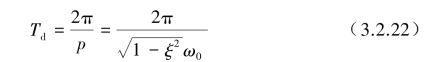
将Td代入式(3.2.21)后得对数衰减率为

当ξ≪1时,近似为
δ=2πξ
(3.2.24)
在对数衰减率曲线上有连续n次振动时,振幅z1,z2,z3,…,zn有如下关系:
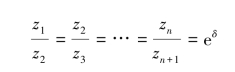
则
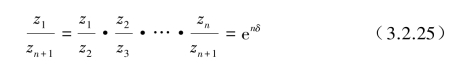
两端取对数得

式(3.2.26)表示,小阻尼下,只要测量衰减振动中的第1次和第n+1次的振幅之比,即可估计出对数衰减率,从而按(3.2.24)确定阻尼比的大小。
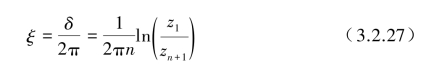
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






