两组随机信号数据可直接从互相关函数的傅里叶变换获得互功率谱密度函数，即

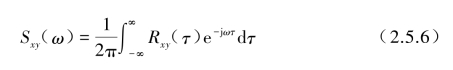
由于互相关函数不是偶函数，故互功率谱密度函数式（2.5.6）可以分解为实部Cxy（ω）和虚部Qxy（ω）两部分。

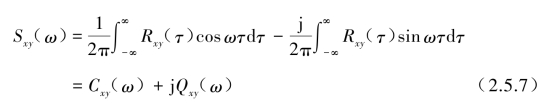
式中，实部Cxy（ω）称为余谱（co-spectrum），虚部Qxy（ω）称为象限谱（quad-spectrum）。

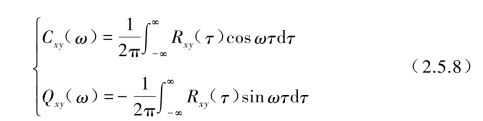
根据上式可知，

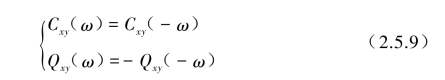
即Cxy（ω）是ω的偶函数，Qxy（ω）是ω的奇函数，同时也可证明Cxy（ω）和Qxy（ω）另一个性质：

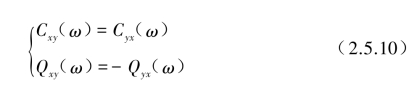
将式（2.5.6）用极坐标表示为

式中，幅值与相位角分别为

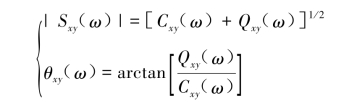
图2.5.3给出了一对典型随机时间历程的互功率谱密度与频率的关系曲线，该图给出了幅值和相位角。(www.daowen.com)

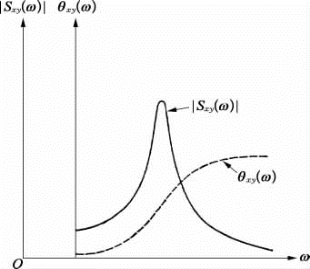
图2.5.3　典型的互功率谱密度

另一个很有用关系式为

为此，互功率谱密度函数用在振动信号处理问题时，常采用相干函数ω）来定义。

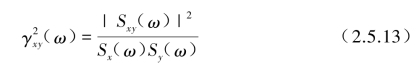
根据式（2.5.12）性质可知：

式（2.5.12）表明了当x（t）和y（t）在统计上如果是完全独立的（或完全相干），则γxy=1；如果是完全不独立的（或完全不相干），则γxy=0。

在实际中主要有以下两方面的应用：

（1）频率反应函数的测量。应用在振动系统测量时可以从振动系统的输入x（t）和输出y（t）信号获得互功率谱密度函数Sxy（ω）和输入自功率谱密度Sx（ω）的关系式中，H（jω）称为振动系统的传递函数，也可以根据式（2.5.15）按H（jω）=Sxy（ω）/Sx（ω）来计算，其置信度可通过相干函数获得。

Sxy（ω）=H（jω）Sx（ω）

（2.5.15）

（2）滞后时间的测量。当振动系统的输入输出之间互谱的相位角为θxy（ω）时，式（2.5.11）表明系统在频率域ω处的相位差，则可得到输入与输出信号之间的滞后时间τ=θxy（ω）/ω。