随机数据的自相关函数主要是描述一个时刻的数据与另一个时刻数据之间的相互关系。对图2.4.3所示样本在时间历程记录x（t）上作在t时刻和（t+τ）时刻之间的相关性估计时，则可以在总时间区间T内由这两个值的乘积对时间t的平均得到。当T趋于无穷时，平均乘积的极限值将接近一个确切的自相关函数。

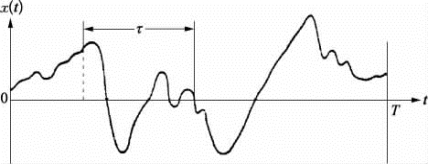
图2.4.3　自相关测量

自相关函数可表示为

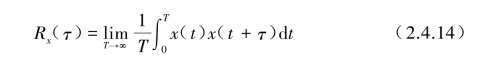
Rx（τ）是恒定的实偶函数，在τ=0时有最大值，即

由Rx（τ）的性质可知，x（t）的均值和均方值为

［例2］ 图2.4.4给出了图2.4.2中4个时间历程所对应的自相关函数R（τ）-时间位移τ的曲线。图2.4.4（a）为一个正弦波Xsin ω0τ所对应的自相关函数：(www.daowen.com)

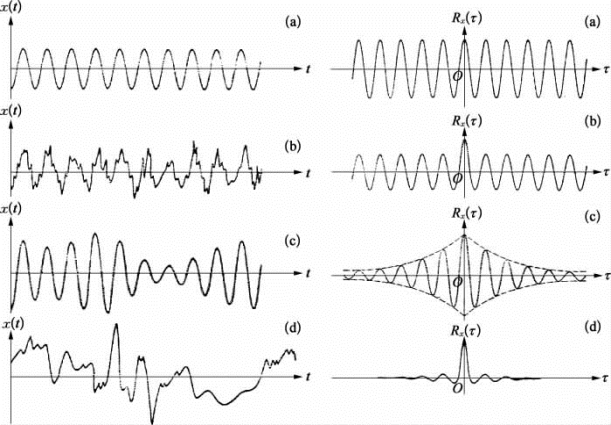
图2.4.4　自相关函数图形

（a）正弦波；（b）正弦波加随机噪声；（c）窄带随机噪声；（d）宽带随机噪声

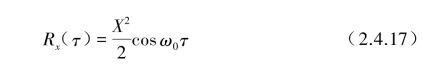
在R（τ）对于时间位移τ历程上，具有与原始正弦波相同的周期（或频率ω0），但其相位角消失了。

图2.4.4（d）是宽带随机数据典型的自相关函数图，R（τ）随时间位移τ很快衰减至零（如均值μx不为零时，则自相关函数衰减到μ2x值）。若是白噪声的极限状况，对应的R（τ）在τ=0处是一个δ脉冲函数。

图2.4.4（b）是正弦波加随机函数所对应的R（τ），这是正弦波的自相关图与随机函数的自相关函数之和。

图2.4.4（c）是窄带随机噪声所对应的R（τ），这是正弦波自相关函数出现衰减形状曲线，当时间位移τ很大时，自相关函数将趋于零（假设μx=0）。该图说明了从正弦波到宽带随机噪声信号，对应自相关函数R（τ）与概率密度函数一样，有明确变化趋势的确定性统计值数据，所以相关函数的功能主要是能够检测和辨别出混淆在随机信号中的确定性信号数据。自相关函数的傅里叶变换是自功率谱密度函数，它们分别表征在时域τ上和频域上的有关信息。