随机数据的概率函数表示瞬时数据值落在某指定范围内的概率。考虑图2.4.1所示的样本时间历程所记录的x（t），对于x（t）值落在x和（x+Δx）范围内的概率可由Tx/T之比得到，这里Tx是在观察时间T内，x（t）落在（x，x+Δx）范围内的总时间，当T趋向于无穷大时，此值将趋于一个确切的概率值Prob。

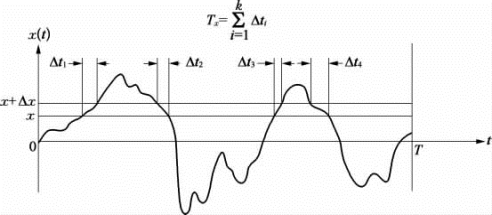
图2.4.1　概率测量方法

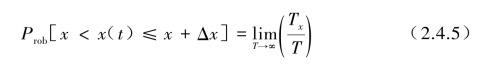
当Δx趋于无穷小时，可用概率密度函数p（x）表示为

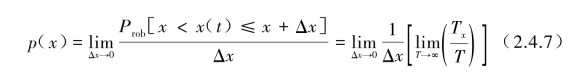
从中可推出p（x）为

瞬时值x（t）小于或等于某值x的概率定义为P（x），它等于概率密度函数p（x）从-∞到x的积分。P（x）称概率分布函数或累积概率分布函数，不应与概率密度函数p（x）相混淆，可表示为

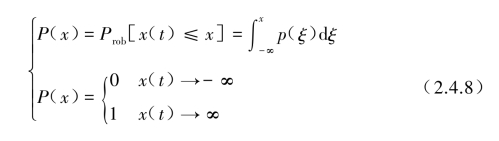
因为当x（t）趋向-∞的概率为0时，x（t）趋向∞的概率为1，所以概率分布函数的值一般应在0与1之间变化。落在任何区域（x1，x2）内的概率为

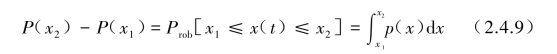
当用概率密度函数p（x）来表示x（t）的均值时，其值为x（t）在所有x值上的加权线性之和，可表示为

(www.daowen.com)

类似的，均方值可认为是x2（t）在所有x值的加权线性之和，可表示为

［例1］ 在实际测量中可能存在的4种样本时间历程记录：①正弦波；②正弦波加随机噪声；③窄带随机噪声；④宽带随机噪声。典型的时程记录如图2.4.2所示。所有记录假设均值为零（μx=0）。

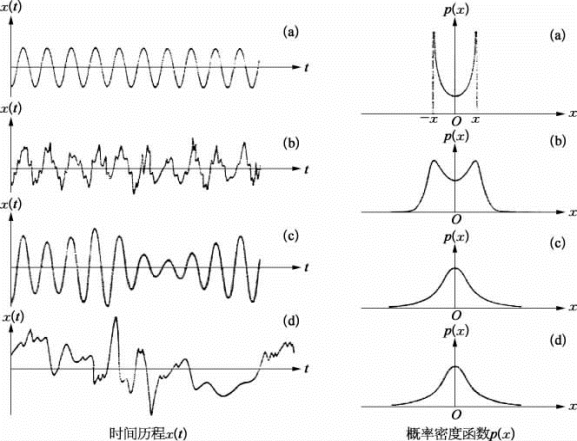
图2.4.2　4个时间历程的概率密度函数

（a）正弦波；（b）正弦波加随机噪声；（c）窄带随机噪声；（d）宽带随机噪声

图2.4.2（a）是正弦波的盆状概率密度函数曲线，对于正弦波曲线x（t）=Xsin（ω0t+θ）的概率密度函数为

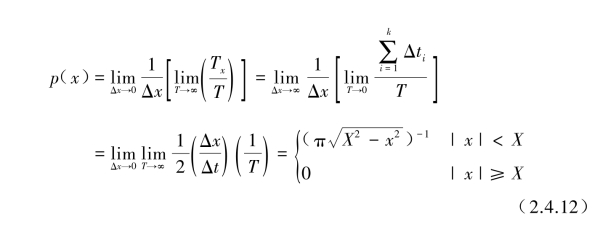
对于图2.4.2（c），（d）所示的铃状概率密度图，分别表示为典型的窄带和宽带随机数据，这些概率密度取为经典的零均值高斯分布形式：

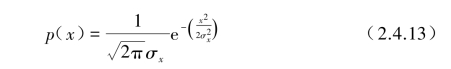
图2.4.2（b）给出了正弦加随机噪声的概率密度图，该曲线具有图2.4.2（a），（c）［或（d）］两种情况的综合特点。

概率密度函数主要应用于描述数据瞬时值的概率，也可以用作确定性数据和随机数据的区分。