【摘要】:类似的对随机过程两个不同时刻之值的相关性(二阶矩),可由t1和两时刻值乘积的总体平均获得,这样随机过程{x}用均值μx和自相关函数Rx来表示,其数学表达式为图2.3.3随机过程的样本函数取总体平均通常情况下,式中μx和Rx是随时刻t的改变而改变的,该随机过程{x}称为非平稳的样本函数。当所有的矩和联合矩均不随时间变化时,则称该随机过程{x}为强平稳,或是严格平稳。
当任何时刻t的特性可以用随机过程样本函数集合的平均值来描述时则可定义为平稳随机过程。
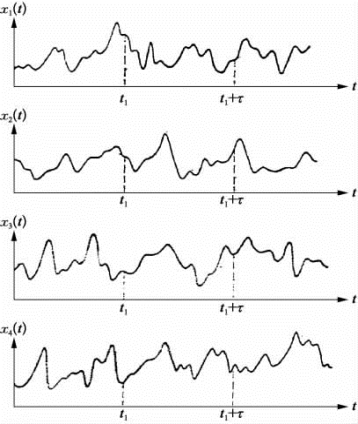
例如,由图2.3.3所示随机过程的样本函数集合(通常也称为总体),随机过程在某一时刻t1上的均值(一阶矩),可以将t1总体中各个样本函数的瞬时值相加,然后除以样本函数的个数而获得总体平均值。类似的对随机过程两个不同时刻之值的相关性(二阶矩),可由t1和(t1+τ)两时刻值乘积的总体平均获得,这样随机过程{x(t)}用均值μx(t1)和自相关函数Rx(t1,t1+τ)来表示,其数学表达式为
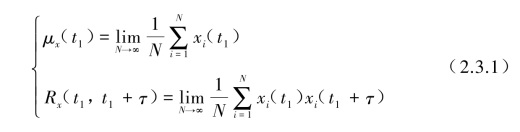
 (https://www.daowen.com)
(https://www.daowen.com)
图2.3.3 随机过程的样本函数取总体平均
通常情况下,式(2.3.1)中μx(t1)和Rx(t1,t1+τ)是随时刻t的改变而改变的,该随机过程{x(t)}称为非平稳的样本函数。只有在特定情况下,当μx(t1)和Rx(t1,t1+τ)不随t1变化时,则该随机过程{x(t)}称为平稳的样本函数,这时对于平稳随机过程的均值μx(t1)=μx是常数,自相关函数Rx(t1,t1+τ)=Rx(τ)只与相关时间τ(或称时间位移)有关。
为了得到描述随机过程的总体概率分布函数,需要计算随机过程{x(t)}中无限个高阶矩和联合矩。当所有的矩和联合矩均不随时间变化时,则称该随机过程{x(t)}为强平稳,或是严格平稳。在许多实际应用中,若能够证明该过程为弱平稳性时,往往也可近似归入强平稳随机过程。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章





