复杂周期数据能用周期性时间变化函数表示为

x（t）=x（t+nTp） （n=1，2，3，…）

（2.2.3）

该函数具有基波的整数倍所组成的波形，与正弦数据相同，其中Tp为一个循环的周期时间，单位时间内的循环数称为“基频ω1（ω1=2πf1）”，显然，正弦数据是复杂周期数据在f1=f0时的一个特例。

复杂周期数据均可以将x（t）展开成傅里叶级数：

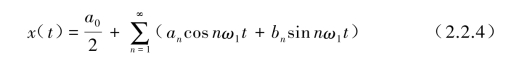
式中，ω1=2πf1=，系数a0=x（t）dt，an=x（t）cosnω1tdt，bn=（xt）sin nω1tdt（n=1，2，3，…）。

式（2.2.4）可用幅值和相位角的另一种形式来表示：(www.daowen.com)

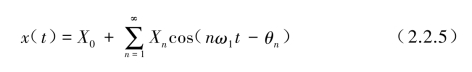
式中，X0=）。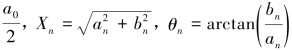

a0表示一个非周期性的并在频域上为0频率的分量，是常数静态项，对动态曲线而言可以被忽略。对式（2.2.5）可以用图2.2.3所示的离散谱来表征。这里要注意，对于复杂周期数据有时只包含几个分量，有时基本分量也可没有。例如某周期函数x（t）只包含60，75，100 Hz，它们的最高公约数为5，故这合成的周期数Tp=0.2 s，即f1=5 Hz，因此展开傅里叶级数时，除n=12，15，20这3项以外，所有Xn值均为零。

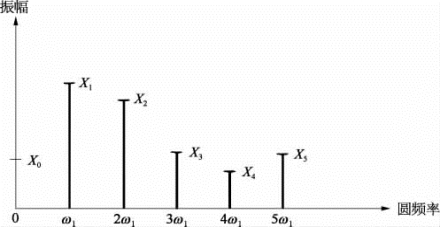
图2.2.3　复杂周期数据谱

本书附录E专门阐述了某些复杂周期函数怎么应用三角级数模型方法。