AHP算法的基本思路就是理清思维，保证决策问题的条理性与合规性。层状决策分析模型的构建可按如下几个步骤进行：决策问题的明晰、选取影响因子建立层状关联、建立判断矩阵、本层次单排序、本层次排序检测一致性、总层次排序检测一致性、单因子总体排序、单因子总体排序检测一致性［153］。

1）决策问题的明晰

为保证对问题结构的层次感，在进行决策分析之前，应对问题有一个整体性的把握。即对于一个具体的问题，率先要明确研究的范围，在这个基础上分析需要完成的终极目标以及为完成这个目标所需要的影响因子，最后形成对问题的总体把握，以便于下一步构建层状分析模型。

2）选取影响因子建立层状关联

我们可以把问题分为由上至下的若干逻辑单元，形成一层状结构。其中最高一层为目标层，只有一个元素，表示在研究范围内需要解决的终极问题；最下一层为措施层，其元素为实现这一目标的基本要素；中间的若干层为基准层以及子基准层，此层元素既可以看成是对目标层元素依据其原理、概念进行的逐层细化，又可以看成是对措施层元素的归并与总结。在具体问题中，往往评权以后需要实测的数据在措施层，因此，对此层元素的划分、选择应严格按照科学合理的原则进行。构建层状模型应注意以下两点：

（1）同层中的各元素不宜过多。过多的元素会导致下一步建立判断矩阵的困难度增加，个别异常元素即会导致一致性检测难以通过，很大程度上，加大了工作难度，降低了工作效率。对具体问题，应依据其情况悉心定夺。

（2）非特殊情况除外，在构建层状决策分析模型时，应根据具体问题的复杂程度划分模型的层次数，假如问题的规模不是很大，我们应当在合理的范围内，尽量减少模型的层次数，子基准过多会导致评价子基准层各元素相对权重的正确性得不到保证，从而使原始数据、知识在计算的过程中模糊、失真，丧失参考价值。(www.daowen.com)

在层状决策分析模型中，如果下层的一个或几个元素与一上层元素存在着某种逻辑联系，即对上层某一影响因子有所贡献，就可建立一条连接，形成一个子层次。下层的一个影响因子可同时对上层若干元素同时建立联系。这里不会涉及个别元素跨层进行的连接，以保证模型中层次的分明。

3）层状决策分析模型实例

如图6－1为一层数为3层的层状决策分析模型，其中A层为目标层；B层为基准层（本模型不含子基准层），共含3个元素；C层为措施层，共含8个元素，其连接方式如图6－1所示。

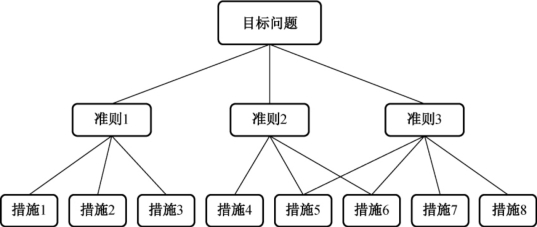
图6－1　AHP层次分析法决策模型

在此模型中，目标层和准则层之间存在三条连接，形成一个子层次：准则层三个元素与措施层之间分别存在3、3、4条连接，可形成3个子层次。其中，措施5同时对准则2、准则3起作用。