在绿色建筑节能与能源评价贝叶斯网络的节点变量和网络模型结构确定的基础上，运用GeNIe软件进行参数学习，得到节能与能源评价贝叶斯网络参数学习的成果，并且得到了好、中、差三种状态的条件概率值。为了对节能与能源评价的影响因素进行进一步的分析和优化，利用贝叶斯网络的推理功能，可以对网络进行正向推理、逆向推理和敏感性分析，以对提高改进绿色建筑设计方案提出策略性的优化建议。

1）正向推理优化

在参数学习完成后，通过改变某一或某些影响因素节点的概率值，在其他节点概率不变的条件下，贝叶斯网络传播可得节能与能源评价的概率值。对比根节点和终节点的概率值的变化方向，可以验证网络模型结果是否成立，同时确定某一或某些根节点对终节点的影响程度，计算方法见公式（4－15）。

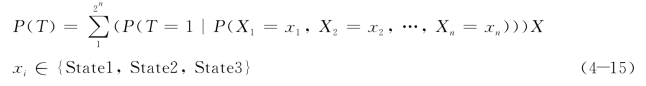
其中，n代表根节点的数量；State1、State2和State3表示根节点的三种状态，即一共有3n种排列方式；公式P（T＝1｜P（X1＝x1，X2＝x2，…，Xn＝xn））代表贝叶斯网络正向传播的条件概率表；P（X1＝x1，X2＝x2，…，Xn＝xn）代表终节点事件的联合概率分布；P（T）代表终节点所在级别的概率值。

如图4－11所示，更改了建筑间距这一根节点的概率值，将其State3的概率值由13%更新为100%，使其完全处于State3状态，随之自然通风性能State3的概率由19%提高到33%，日照与遮挡State3的概率值由58%提高到76%，终节点绿色建筑节能评价的State3的概率值也由49%更新为62%。可看出建筑间距越大，自然通风性能越好，日照与遮挡性能越好，绿色建筑节能评价值越高，可得出因素之间呈正相关。

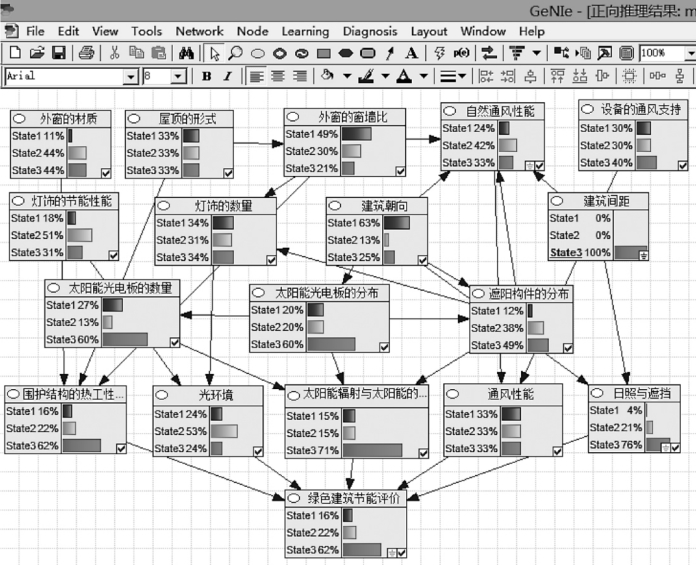
图4－11　正向推理优化图

2）逆向推理优化

一般的推理分为两类：精确推理和近似推理。精确推理应用在简单的小规模贝叶斯网络，近似推理可应用在复杂的大规模贝叶斯网络。逆向推理即是在设定最终节点概率值的基础上，反推根节点的条件概率值。可设定终节点的等级为好、中、差中的一种，并设置此等级的概率值为100%，计算某一根节点的后验分布。假设设置终节点的状态为差，即属于第一级别，可求得某一节点处于State1、State2和State3的概率，计算方法见公式（4－16）。

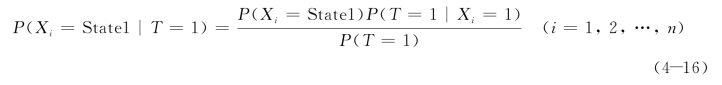(www.daowen.com)

如公式（4－16），当Xi＝State2和Xi＝State3时，即可计算i节点处于State2和State3的概率。i节点所处状态的级别和建筑节能与能源评价的级别正相关，如果终节点处于第一级别，只要确定所有节点里第一级别概率值最大的节点，就可以进行逆向推理分析。

如图4－12所示，将终节点设置为最高级，逆向推理各根节点的变化。可看出各节点State3的概率值都有所提高，其中，围护结构的热工性能、光环境State3的变化达到或超过了15%，变化显著。追溯到三级指标，State3变化值超过12%的指标由大到小的排序为：遮阳构件的分布、设备的通风支持、外窗的材质、外窗窗墙比、太阳能光电板的数量、建筑间距、自然通风性能、建筑朝向。说明当想提高绿色建筑节能效果时，可依次通过改变上述因素，效果会更明显。

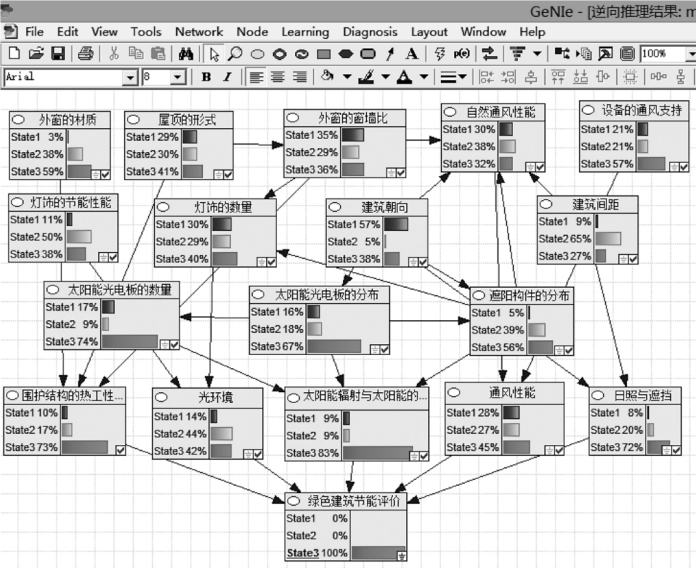
图4－12　逆向推理优化图

3）敏感性分析

敏感性分析是分析计算网络根节点变化时，终节点的变化情况，找出对终节点影响较大的根节点。根节点分为两类：敏感节点和非敏感节点。敏感节点是自身变化小，导致终节点发生较大变化的节点；非敏感节点是自身变化小，导致终节点变化也小或是终节点没有变化的节点。敏感性分析通过确定敏感节点，进而在实际应用中对其重点观测。数学定义如下：

假设e表示情境，h表示假设，目的是分析情境e对成果P（h｜e）影响程度的敏感度，若P（h｜é）≈P（h｜e），那情境é∈e是充分的，通过计算每个é∈e的P（h｜é）的值，确定h变化较大的值。贝叶斯网络可以在软件中进行敏感性分析的计算，确定某一根节点对终节点的影响程度。

如图4－13所示，即是贝叶斯网络模型的敏感性分析结果，深色的方框表示敏感因素。可看出，自然通风性能、遮阳构件的分布、太阳能光电板的数量、灯饰的数量、太阳能光电板的分布对建筑节能性能影响明显。因此，在建筑设计时，应重点关注这些因素的指标设置，以实现设计方案的优化。

图4－13　敏感性分析结果图