信息论是关于信息的理论，是专门研究信息的有效处理和可靠传输一般规律的科学。20世纪40年代后期，香农发表的《通信的数学理论》等论文，第一次为通信过程建立了数学模型，这就是现代信息论的开始。

信息论采用数理统计与概率论的方法，研究信息传输、信息压缩、信息熵、信息系统等问题，用以计算信息系统信道容量。

香农-哈特利（Shannon-Hartley）定理描述的就是信道容量与信道带宽以及信道信噪比关系的。其公式（也称香农公式）表示为

C=B·log2(1+S/N)　(2.1)

式中：C为信道容量，b/s；B为信道带宽，Hz；S/N为信噪比，dB。

可以假设S/N≫1，并定义SNR=10log2 S/N，那么可以用近似值表示为

C=1/3·B·SNR　(2.2)(www.daowen.com)

香农-哈特利定理也称为有噪信道编码定理，这个关系式就是信道编码技术的基础原理。信道编码的目的是通过编码技术减少比特错误，从而提升SNR和提高信道容量。另外，从式（2.1）可以看出，如果信噪比一定，增加带宽也可以提高信道容量，这就是扩频通信的基本原理。

式（2.2）的意义可以用图2.5中的曲线来表达。C/B（容量/带宽），单位为b/s/Hz，即单位频带的信息传输速率，其物理意义就是频带的利用率。一般情况下，信道资源都是有限的，因此尽量提高C/B值，追求频带利用率能达到的极限，是现代信息技术和通信技术主要的工作目标。

随着通信技术日新月异的发展，以及各种新型学科的相互渗透，信息论的研究已经演变成为一个“信息科学”的学科体系，不再局限于香农当年狭义的通信系统的数学理论的研究。但信息论的研究与发展仍然是现代通信行业的基础和重要支撑。

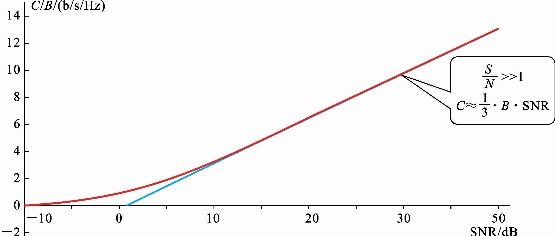
图2.5　香农-哈特利定理的近似表达