如图6.3.8所示，在路堤与桥台连接处，为保护桥台后路基不受冲刷，桥台两侧筑成锥体形的填土并用石料铺砌锥体表面，称为锥体护坡。

锥体护坡坡脚及基础通常为椭圆形曲线，基边坡按规定，当路堤填土高度小于6 m时，锥体坡度平行于线路方向为1∶1，横向垂直于线路方向的坡度1∶1.5，大于6 m时，路基面下超过6 m部分纵向坡度由1∶1变为1∶1.25，横向坡度1∶1.5变为1∶1.75。

锥体护坡的放样，可先求出坡脚椭圆形的轨迹线，然后依此测设到地面上。

此法适用于锥坡不高，干地，底脚地势平坦。桥涵中心与水流方向正交的情况下，用椭圆曲线放样时，也可采用此法。

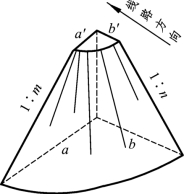
图6.3.8　锥体护坡

1.内侧量距法

已知锥坡的高度为H，两个方向的坡率分别为m、n，则椭圆的长轴a＝mH，b＝nH。在实地确定锥坡顶点O的平面位置后，以O点为圆心，放样出以a、b为半径的同心圆的1/4（当地形平坦时，可用拉绳放样），过O点拉直线，与同心圆分别相交于I、J两点，过I、J两点作平行于x、y轴的直线，交于P点。P点即为以O为圆，以a、b为长短轴的椭圆上的点，如图6.3.9（a）所示，以此就可以在实地放样出锥坡底脚与基础的边缘线。由于P点为椭圆上的任意点，设P点坐标为（x，y）。将长轴a分为n等份（等份越多，椭圆连线越平顺），相应于n等份的坐标y值，可按椭圆方程导出下式进行计算：

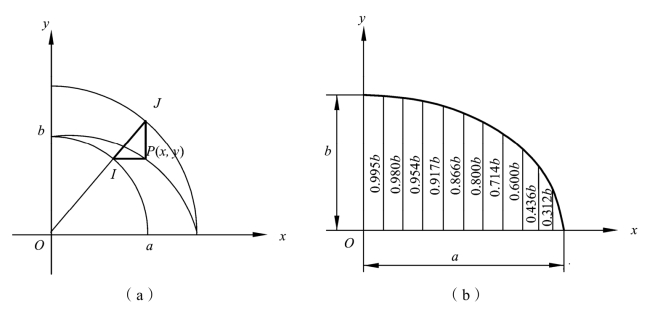
图6.3.9　内侧量距法

(www.daowen.com)

一般情况下，取n为10即够用，每一等份的长度为a/10，假定每一等份，则n1＝0.1a，则y1就等于0.995b，依此类推，就可以将其他n－1个点的坐标（xi，yi）求出，将其连起来就为椭圆曲线的轨迹线，如图6.3.9（b）所示。

2.外侧量距法

在桥涵施工中，为了减少回填工作量，路堤填土往往将开挖弃土放在锥坡位置，用内侧量距法不易放样锥坡，这时就需要平移x、y轴的方法，从椭圆曲线的外侧向内侧量距。

以1/4椭圆的长短轴a、b为直角坐标系的x、y轴，椭圆上的一点P的坐标为（x，y），如图6.3.10所示，在Ox轴上用钢尺将a分为n等份，且直尺按平行于椭圆短轴b的方向，量出各点相应的y′值，y′＝b－y，依此可以放样出椭圆曲线上的一系列点，然后将其连接起来，就形成了锥体护坡的底脚边缘线。

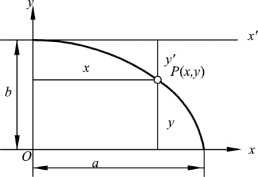
图6.3.10　外侧量距法

当遇到斜交桥涵锥坡放样时，也可应用此法，但不能直接应用，必须依照桥台或涵洞轴线与线路中线的夹角α（即斜度），将a值乘以不同的斜度系数C。斜度系数C可按下式计算：

由于坐标量距法的常数值不因锥坡的变化而改变，施工人员只需要记住 10 个常数，知道椭圆短轴值，就可以在现场计算出椭圆曲线上的各点，定出曲线来，另外在其放样时，方法和器具都比较简单，且容易掌握，积聚以上优点，此法在桥涵锥体护坡施工中较常用。