1.偏角法测设圆曲线的基本原理

偏角法是传统曲线详细测设的方法之一。偏角是指过置镜点的切线与置镜点到测设点的弦长之间的夹角，几何学中称为弦切角。

如图4.4.2所示，偏角法测设曲线的基本原理是根据偏角δ 和弦长C交会出曲线点。例如置镜于ZY点，于切线方向拨偏角δ1的方向与C1距离定1点，拨偏角δ2的方向与C2距离定2点，同样方法可测设曲线各点。

2.圆曲线偏角计算

如图4.4.2所示，设弧长为li，根据几何原理偏角δi等于弧长li所对圆心角φ 的一半。

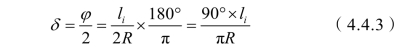
式中 R——圆曲线半径；

li——置镜点至测设点的曲线长。

由于按照整桩号测设，所以在靠近ZY、QZ、YZ的点与主点间的曲线长均不足规定中桩间距，则对应的偏角称为分弦偏角。规定中桩间距所对应的偏角称为整弦偏角。当测设点为等分段时，偏角计算有如下规律：

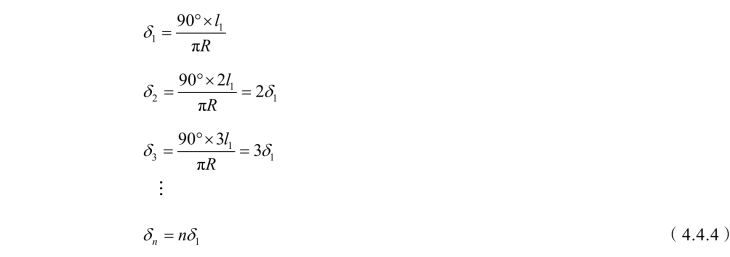
等分段时，曲线上各点的偏角均为δ1的倍数。

圆曲线弦长计算式为：

3.偏角法测设圆曲线举例

测设曲线时，由于拨角、量距误差的影响，曲线较长时，为了防止误差积累过大，一般是从两端主点ZY、YZ测至QZ，在曲中点闭合校核。计算偏角时，应注意正拨与反拨。以过置镜点的切线为准，顺时针拨角称为正拨或顺拨，其偏角为正拨偏角值。逆时针拨角称为反拨，其偏角为反拨偏角值。反拨偏角值＝360°－正拨偏角值。

曲线半径很大时，20 m弧长与相对应的弦长相差极微，测设中可不考虑弧弦差，将弧长视为弦长。半径较小时，测设中应考虑弧弦差的影响，用式（4.4.5）计算弦长。

【例4.4.2】 按例4.3.1提供的曲线资料举例如下。

【解】（1）偏角计算：

① 置镜于ZY点测至QZ各点的偏角计算，见表4.4.1结果。

表4.4.1　圆曲线正拨偏角资料表(www.daowen.com)

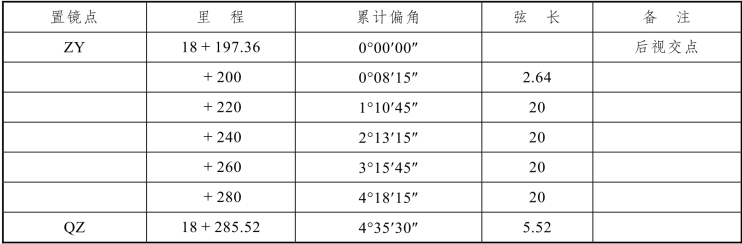
② 置镜于YZ点测至QZ各点的偏角计算，见表4.4.2结果。

表4.4.2　圆曲线反拨偏角资料表

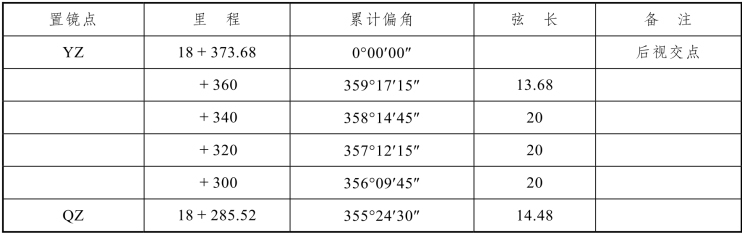
（2）测设方法：

以置镜ZY点为例说明测设方法：

① 置镜于ZY点，对中、整平，以盘左后视JD，度盘配置为0°0′00″。

② 松开照准部制动，顺时针转动照准部，是水平读盘读数为第1点偏角值0°08′15″，制动照准部。

③ 从ZY点起，在视线上量第1段弦长2.64 m，打入木桩得第1桩点。

④ 继续转动照准部，是水平读盘读数为第2点偏角值1°10′45″，制动照准部。从第1桩点量第2段弦长20 m。由司镜者指挥前尺手使20 m端点的线铊与视线重合，即为第2点，打入木桩。

⑤ 同上述方法，依次测设各点至QZ点。在曲中点检核。

表中计算校核：累计偏角＝4°35′30″与QZ偏角＝α/4＝4°35′30″相等，计算无误。

4.检核曲线测设精度

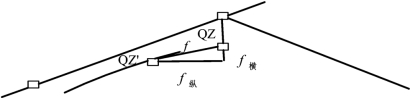
曲线测设中，由于拨角和测设距定点等误差的影响，用偏角法测设的曲中点与主点测设时的曲中点常常不能重合。如图4.4.3所示，由ZY测至QZ假设落在QZ′的位置上，则QZ′→QZ的距离f称为曲线闭合差。将f闭合差分解为两个量，沿线路方向的分量称纵向闭合差f纵，沿曲线半径方向称横向闭合差f横。纵向误差是相对误差，是沿中线方向的误差，对工程影响较小。横向误差是绝对误差值，垂直于中线，对工程影响较大。影响曲线闭合的因素较多，诸如切线丈量误差、拨角误差、弦长丈量误差等。因此测设时，应提高切线丈量精度，测设中线点时，定了方向后，丈量弦长，应由司镜者再次观测前点线铊，使垂线精确位于视线上，确保线铊落点准确。曲线越长，累计误差越大，对于长大曲线，多设控制桩，分段闭合。曲线测量限差如表4.4.3所示。

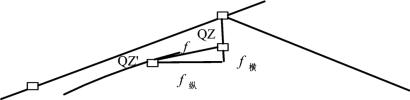
图4.4.3　曲线闭合差

表4.4.3　距离偏角测量闭合差