1）基础沉降变形规律

图244为建筑物基础沉降变化曲线。对比三种工况下基础沉降曲线可以看出，纵墙开洞率的大小对建筑自身刚度有直接影响，进而对其沉降变形有一定的约束作用，但三者变化趋势大致相同，且协调作用在建筑物跨越坑外土体沉降槽最低点及上凸区域曲率最大点位置时最为明显。以D=1m为例，纵墙开洞比为13%时，建筑物沉降最大，其值为12.8 mm；开洞比为30%和40%时，建筑物沉降次之，其值分别为12.2 mm、11.9 mm。尽管三种工况下建筑物沉降趋势均呈现明下凹形态，但受开洞比影响时，其沉降挠曲程度存在差异。开洞比为40%时，其沉降挠曲程度最大。

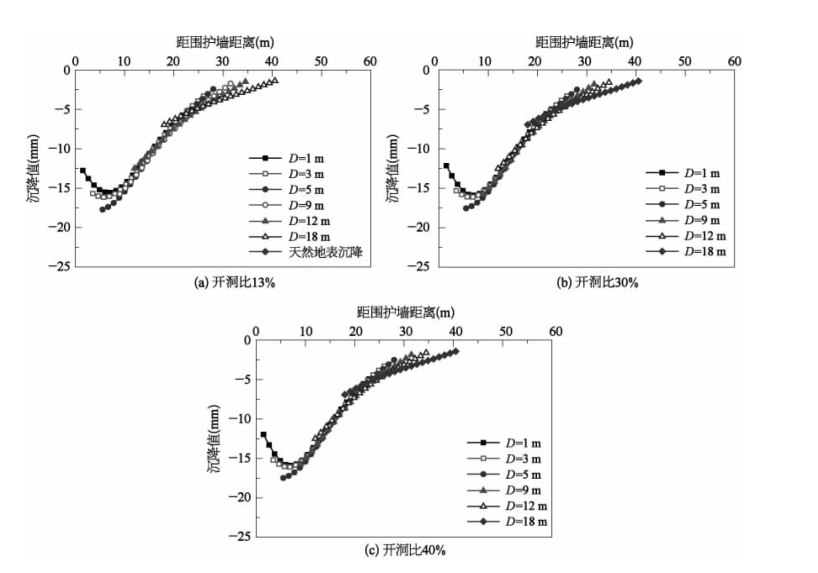
图2-44　建筑物基础沉降变化曲线

2）基础相对挠曲变形规律

图2-45为建筑物基础相对挠曲变形曲线。

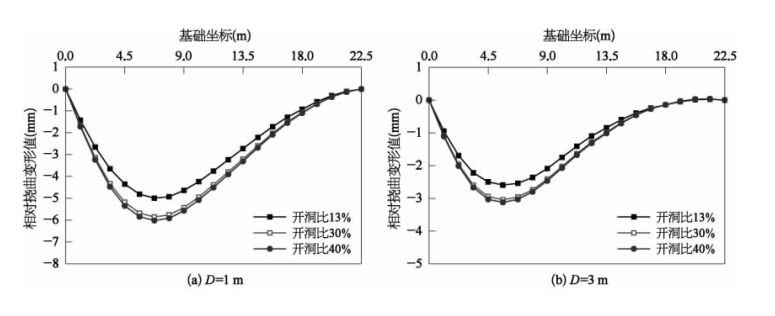
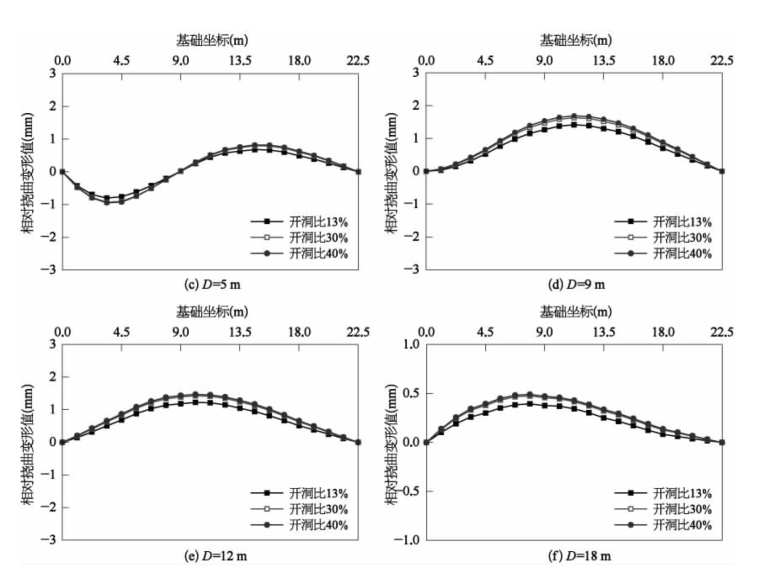
图2-45　建筑物基础相对挠曲变形曲线

三种开洞比条件下，当D=1 m和D=3m时，纵墙基础相对挠曲均呈现下凹形态，且相对挠曲变形值随着建筑物整体刚度的增大而减小。其中，当D=1 m时最为明显，纵墙开洞比为40%时，相对挠曲变形值最大，其值为6.02 mm；开洞比为30%时，相对挠曲变形值次之，其值为5.85 mm；开洞比为13%时，相对挠曲变形值最小，其值为5 mm。当D=5 m时，纵墙基础相对挠曲呈现“∽”形态，其特点为下凹相对挠曲发生在建筑邻近基坑开挖面一侧，上凸相对挠曲发生在建筑远离基坑开挖面一侧；随着纵墙开洞比的增大，建筑物整体刚度减小，纵墙近基坑开挖面侧的下凹相对挠曲最大值逐渐增大，其相对挠曲峰值分别为0.8 mm、0.9 mm、1 mm；远基坑开挖面侧的上凸相对挠曲变形最大值逐渐增大，其相对挠曲峰值分别为0.68 mm、0.8 mm、0.84 mm。当D≥9 m时，纵墙基础相对挠曲主要呈现上凸形态。此外，当D=9 m时，即建筑物跨越坑外沉降槽上凸挠曲曲率最大点时，此时纵墙基础上凸形态的相对挠曲最大，相对挠曲变形峰值也随着建筑物整体刚度的减小而增大，开洞比为40%时对应值最大，值为1.7 mm；开洞比为13%时对应值最小，值为1.42 mm。当D≥18 m时，建筑物因远离土体开挖面而受其开挖影响较小，三种开洞比的建筑物纵墙基础相对挠曲峰值差异较小。

此外，纵墙基础相对挠曲变形峰值的出现位置并没有因建筑物纵墙开洞比的改变而发生变化，但其峰值的大小存在明显差异。

3）建筑纵墙主拉应变变化规律

基于2.6.1节工况4～工况6条件，列举了不同开洞比条件下建筑物纵墙主拉应变的变化规律，如图2-46～图2-48所示。

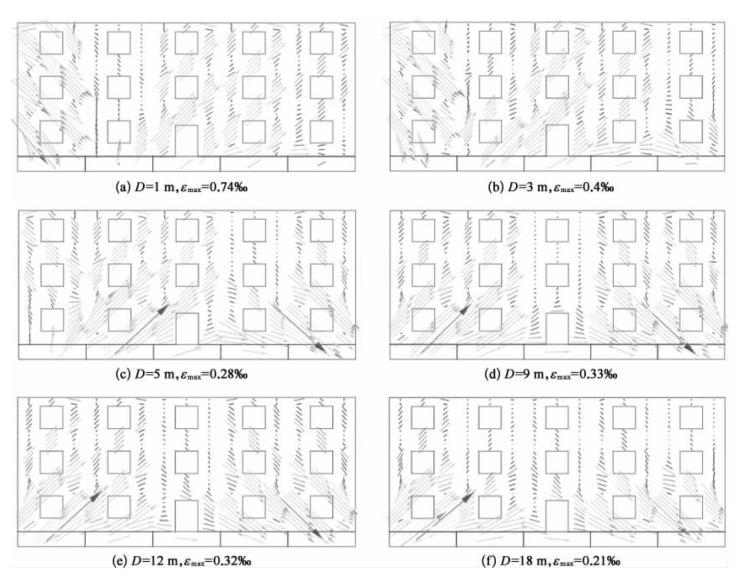
图2-46　纵墙墙体主拉应变矢量图（工况4）

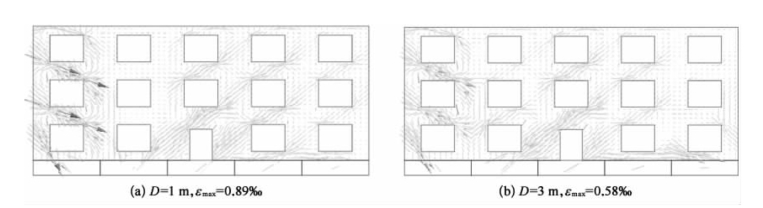
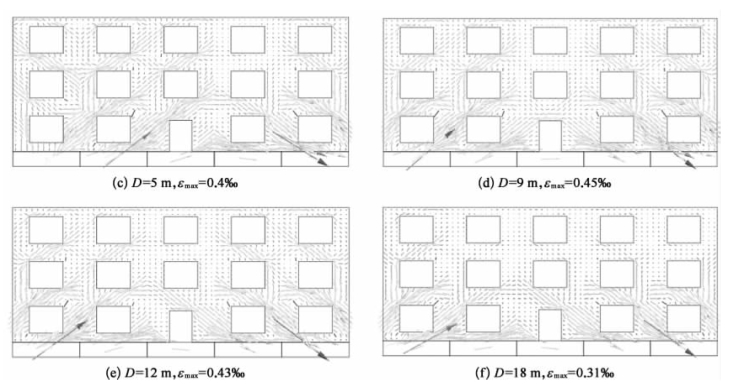
图2-47　纵墙墙体主拉应变矢量图（工况5）(www.daowen.com)

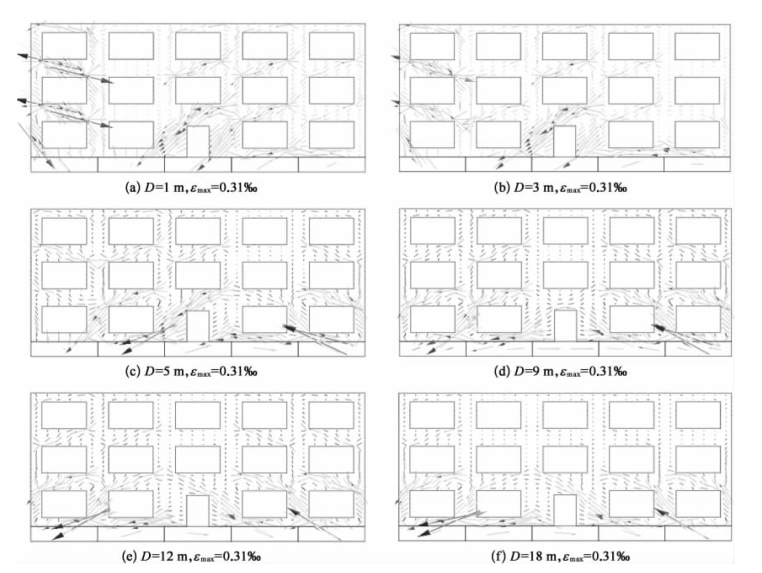
图2-48　纵墙墙体主拉应变矢量图（工况6）

由图可知，三种工况下，当D=1 m时，建筑物相对挠曲均呈现下凹形态，纵墙主拉应变大致呈45°，主要分布于纵墙位于地层沉降槽最大值的两侧，分布特点如下：①开洞比为13%时，纵墙主拉应变分布较为均匀；开洞比为30%时，门、窗与纵墙交接处的主拉应变集中现象明显；开洞比为40%时，墙体主拉应变集中在门、窗与纵墙交接处，且出现反方向形态；②开洞比为30%和40%时，1层墙体主拉应变集中现象较开洞比为13%时更为明显。当D=5 m时，纵墙“∽”形态的相对挠曲使得纵墙近基坑开挖面一侧和远基坑开挖面一侧均产生大致呈45°方向的纵墙主拉应变。窗间墙依然为应变较为集中区域，且远基坑侧墙体拉应变明显大于近基坑侧墙体拉应变。当D≥9 m时，纵墙的因上凸形态的相对挠曲使得其两端位置产生大致45°方向的主拉应变。

对比三种工况下纵墙主拉应变可知，随着建筑物纵墙开洞比的增大，建筑物纵墙的主拉应变峰值先增大后减小。当D=1 m和D=9 m时，建筑物跨越坑外土体沉降槽最低点及上凸区域曲率最大点位置时，建筑物纵墙分别呈现下凹和上凸形态相对挠曲，且变形最为明显。当开洞比13%时，建筑物刚度较大，相对挠曲变形较小，对应最大主应变为0.74‰、0.33‰。开洞比30%时，建筑物刚度因墙体开洞率的增大而减小，相对挠曲随之增大，对应最大主应变为0.89‰、0.45‰。开洞比40%时，建筑物刚度最小，相对挠曲达到最大，但此时受填充墙面积的影响，其最大主应变仅为0.59‰、0.37‰。当D=3m时，三种工况对应的最大主应变分别为0.4‰、0.57‰、0.41‰。当D=5 m时，三种工况对应的最大主应变分别为0.28‰、0.4‰、0.22‰。当D=12 m时，三种工况对应的最大主应变分别为0.32‰、0.43‰、0.36‰。当D=18 m时，三种工况对应的最大主应变分别为0.21‰、0.3‰、0.25‰。由此可知，纵墙主拉应变主要受建筑物相对挠曲变形和自身开洞比影响。

通过建立基坑-建筑物三维有限元数值模型，分析不同结构形式浅基建筑受基坑开挖影响，揭示了建筑物与地层相互作用的变形特征。建筑物结构形式包括开放式框架、填充式框架及砌体结构。此外，针对填充式框架，重点分析了开洞比对建筑物整体变形的影响。结果表明：

（1）随着建筑物逐渐远离基坑开挖面，建筑物相对挠曲形态将逐步由下凹变形形态转变为“∽”变形形态，最后呈现为上凸变形形态，且当建筑物跨越坑外沉降槽最低点及上凸曲率最大点时，相对挠曲最为明显。

（2）当建筑物为不同结构形式时，建筑物整体刚度存在明显差异，其中填充式框架整体刚度最大，开放式框架次之，砌体结构整体刚度最小。因此受建筑物整体刚度影响，砌体结构对应的角变形及墙体主拉应变最大，开放框架次之，填充框架最小。对比不同墙体开洞比条件下填充框架墙体主拉应变分布规律可知，墙体主拉应变峰值及方向受开洞比影响存在明显差异。

（3）α为任意角度时，建筑物墙体将发生倾斜。当D值为定值时，建筑物纵墙的倾斜随着夹角α的增大逐渐增大，横墙倾斜变化规律则反之。当α为定值，纵墙倾斜值则随着D值的增大而呈现出减小趋势，横墙倾斜峰值则发生在D=9 m处。

（4）当α≠90°时，建筑物将产生横、纵向水平位移，且当D值保持不变时，其横、纵向水平位移最大值均随着其角度α的增大逐渐减小。当建筑物与基坑边夹角相同时，其横、纵向水平位移最大值则随着其与基坑边水平距离D的增大，而先增大后减小，水平位移最大值出现在D=5 m处。

（5）当D=1 m时，正立面纵墙相对挠曲呈单纯的下凹形态。除α=30°所对应正立面纵墙发生较明显的下凹挠曲变形外，建筑物正立面纵墙随着与水平距离D的增大，将逐步转变为“∽”形，上凸挠曲变形。正立面纵墙下凹形态的相对挠曲变形最大值和上凸形态的相对挠曲变形度最大值分别发生在α=90°且跨越坑外土体沉降最大点和上凸挠曲曲率最大点值位置。

（6）当α≠90°时，建筑物整体结构将会发生扭转变形，并且伴随着建筑物逐渐远离基坑开挖面，建筑物将逐步由逆时针扭转变形转变为顺时针扭转变形，并且当D=1 m且α=30°所对应的结构扭转变形最为显著。

（7）当α为任意值时，正立面框架邻近基坑开挖一侧梁、柱端弯矩均较大，而背立面框架除α≠90°时，远离基坑一侧的梁、柱弯矩值均较大。1层柱弯矩则沿①轴至⑤轴由柱底弯矩为正值，柱顶弯矩为负值转变为柱底弯矩为负值，柱顶弯矩为正值。2～3层柱弯矩变化规律反之。

（8）当α为任意角度时，其纵墙将在扭转、挠曲变形的协同作用下产生相应的主拉应变。建筑物正立面纵墙最大主拉应变发生其跨越坑外土体沉降槽最低点和上凸挠曲曲率最大点位置处，挠曲变形将起主要影响作用。建筑物背立面纵墙最大主拉应变则发生D=5m处，此时建筑物挠曲、扭转变形的协同作用成为主要影响因素，由此说明，一般大小的复合变形作用同样会降低邻近建筑结构的可靠性。

（9）梁、柱刚度损伤直接影响建筑物整体刚度，从而决定了其对基坑开挖面外部土体位移场约束作用的强弱，但二者的变形规律大致相同。

（10）梁、柱同时损伤且在某一损伤刚度条件下，建筑物随着距离D的增大，纵墙相对挠曲均逐步由下凹形态转变为“∽”形态，最终表现为上凸形态。当梁、柱刚度损伤较小时，建筑沉降曲线近似直线分布，原因在于建筑刚度的协调作用较为明显，其相对挠曲变形和纵墙拉应变较小；随着梁、柱刚度损伤的增大，建筑物整体刚度逐渐减小，其对基坑开挖面外部土体沉降变形的抑制协调作用亦随之减弱，建筑物沉降曲线将逐步呈现出较为明显下凹和上凸形态。当梁、柱损伤较大时，其下凹形态和上凸形态相对挠曲最为明显，与之对应的墙体主拉应变亦随之增大，但墙体的拉应变分布趋势与峰值出现位置基本保持不变。

（11）梁、柱刚度分别损伤条件下，建筑物相对挠曲呈现下凹形态时，梁刚度对加强建筑整体刚度的作用明显高于柱的作用。当建筑相对挠曲呈现上凸形态时，柱刚度对加强建筑整体刚度的作用明显高于梁的作用。