为研究房屋结构的扭转变形规律，将采用如下计算方法：首先分别将正、背立面纵墙所对应的沉降值各自与其对应的最小沉降值作差，然后将两者所得结果进行差值，将此差值定义为建筑结构的扭转变形。

当α≠90°时，由于建筑物正、背立面纵墙存在差异沉降，因此建筑物不仅发生相对挠曲变形，同时建筑物还将发生不同程度的扭转变形，为形象地了解扭转变形性状，本节选取了不同施工距离条件下任意角度建筑物的沉降云图，如图2-12～图2-15所示。

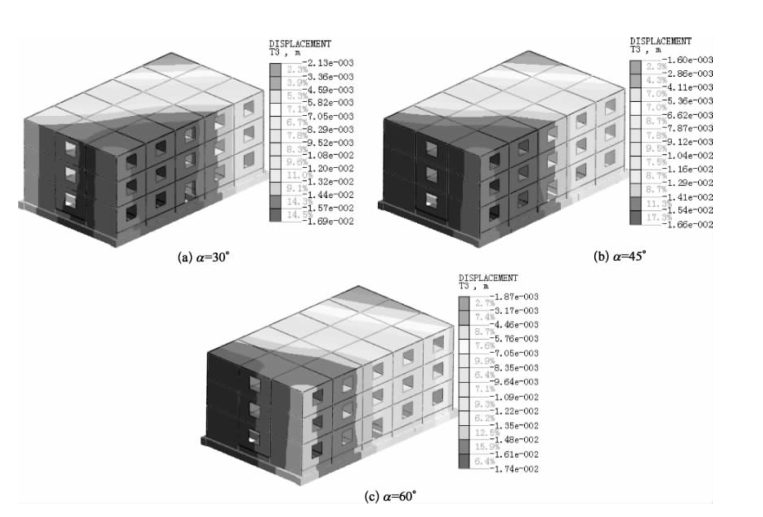
图2-12　D=1m时建筑物任意角度沉降图

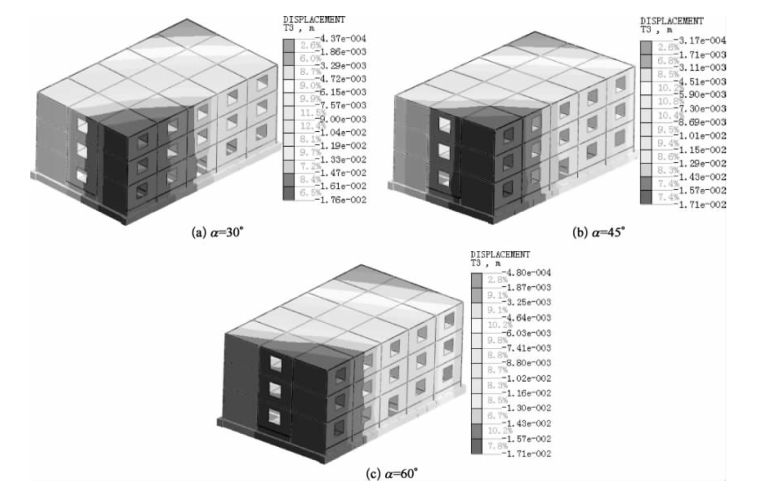
图2-13　D=5m时建筑物任意角度沉降图

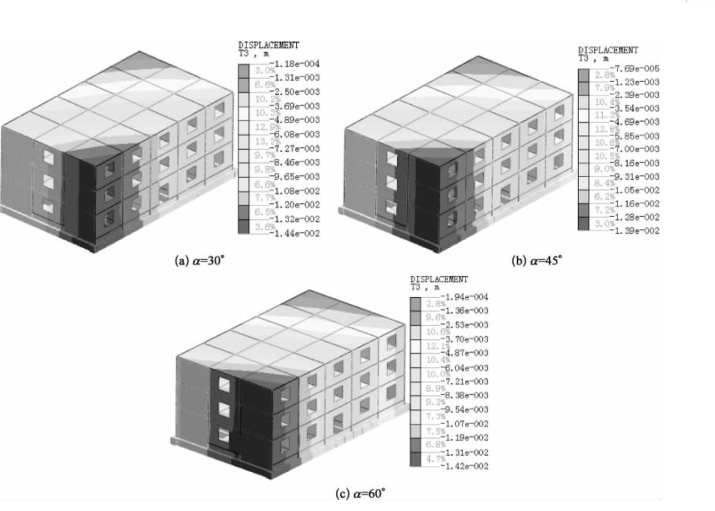
图2-14　D=9m时建筑物任意角度沉降图

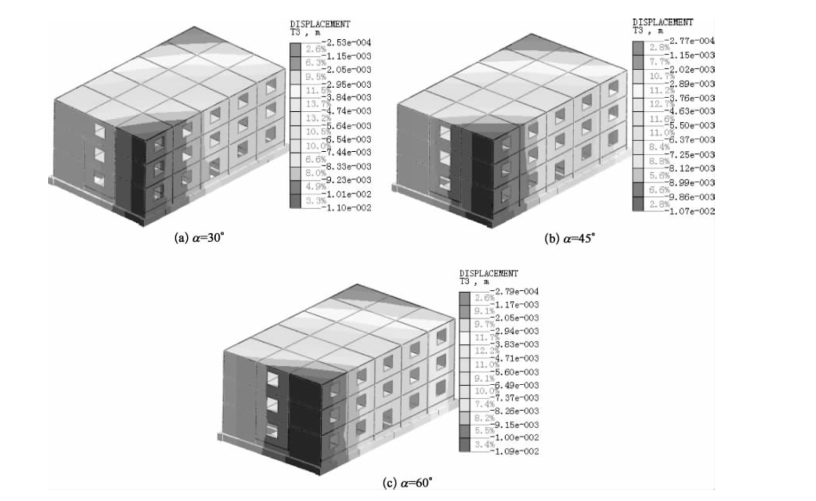(www.daowen.com)

图2-15　D=9m时建筑物任意角度沉降图

由图2-12～图2-15可知，建筑物整体沉降趋势随着其与基坑角度的改变而呈现明显差异。以D=5为例，当α=30°时，建筑物17.6～14.7mm的沉降主要集中在参考点转角附近，其中正立面纵墙较大沉降最为集中。当α=45°时，建筑物17.1～14.3 mm的沉降主要集中在参考点转角附近，大致成对称分布。当α=60°时，建筑物17.1～14.3 mm的沉降集中区域逐步有参考点两侧转移到邻近基坑侧横墙。对比不同角度时建筑物的沉降分布发现其沉降分布趋势始终与基坑开挖面保持平行，这表明坑外土体的不均匀沉降作用使得建筑物发生一定程度扭转。

图2-16所示为纵墙扭转变形曲线。

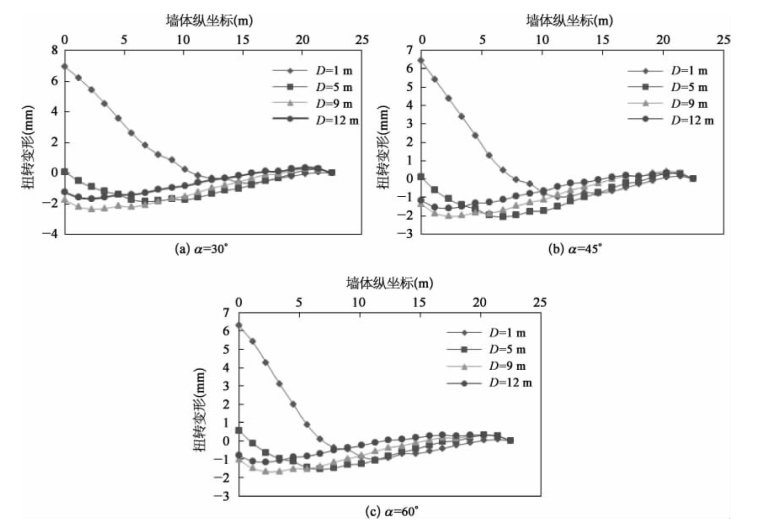
图2-16　纵墙扭转变形曲线

由图2-16可知，当D=1 m时，建筑物的下凹挠曲变形将使得其发生逆时针扭转变形，其扭转变形将随着与基坑开挖面之间角度的增大而逐渐减小。当α=30°时，扭转变形最大，其峰值为6.9 mm。当α=45°时，扭转变形次之，其峰值为6.5 mm。当α=60°时，扭转变形最小，其峰值为6.3 mm。当夹角α保持不变时，建筑结构均在D=1 m时扭转变形达到峰值。

D≥5 m时，建筑物的上凸挠曲变形将使得其发生顺时针扭转变形，并且α保持不变时，伴随着水平距离D的增大，建筑结构的扭转变形先增大后减小。以α=30°为例，当D=5m时，建筑结构顺时针扭转变形的峰值达到-1.83 mm。当D=9 m时，建筑结构顺时针扭转变形达到最大，其峰值达到-2.33 mm。当D=12 m时，建筑结构顺时针扭转变形有所减小，其峰值达到-1.65 mm。当角度α为任意值时，建筑结构扭转变形峰值出现位置略有不同。当α=30°且D=9 m，建筑结构所对应扭转变形最为显著，峰值达到-2.33 mm。当α=45°时且D=5 m时，建筑结构所对应扭转变形最为显著，峰值达到-2 mm。当α=60°且D=9 m，建筑结构所对应扭转变形最为显著，峰值达到-1.68 mm。