1.影响结构刚度的主要因素

对于结构设计人员来说，对第一极限状态（承载力极限状态）的设计都很熟悉，也特别重视它，因为一旦结构破坏，丧失承载能力或结构失稳、倾覆等都将造成生命和财产的重大损失，而对于结构的刚度和变形问题有时重视不够。应当指出，结构变形问题也会直接影响房屋建筑的正常使用，过大的变形会使装饰材料开裂甚至剥落，影响电梯正常运行，直接影响加工车间的产品加工精度，严重时还会使人感到不适。随着高层建筑的发展，房屋越来越高，更由于高强度材料的应用，结构构件的截面做得更小、更细，因此结构的刚度和变形问题就越来越突出，在设计中应当予以足够的重视。

在第1章中已经提到刚度是产生单位变形所需要的力。应当指出，这里所指的“变形”和“力”都是广义的，“变形”可以是位移、应变、曲率、剪切角、扭转角等，“力”可以是轴力、应力、弯矩、剪力或扭矩等。单位“力”作用下的“变形”为柔度，柔度和刚度互为倒数。

在结构设计中通常要用到截面刚度、构件刚度、结构刚度等概念，关于截面刚度在第1章中已经介绍，这里再讨论结构的刚度与变形。

前面已经提到，构件刚度是指构件在指定方向上引起单位变形所需的荷载。以单跨梁为例，悬臂柱在柱顶水平力作用下的变形为

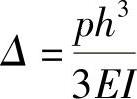
当Δ=1时所需的力为3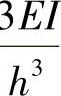，即为构件刚度，当p=1所产生的位移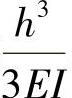，为构件柔度。

又如受均布荷载下的简支梁，其跨中挠度为

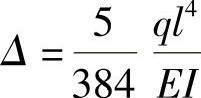
则其刚度为3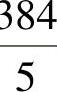·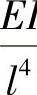I。

由上两个例子可见，影响刚度及位移的主要因素有：

1）截面的几何性质，即几何特征，有：面积A、重心位置C_x、惯性矩I_x、截面模量W_x等。

2）材料力学性质，主要是弹性模量E、剪切模量G等。

3）与构件的支承条件及受荷载性质有关，如是均布荷载还是集中荷载，是固端支承、铰支承，还是自由端等。

关于典型单跨梁（简支梁、固端梁、悬臂梁）的最大内力与位移的计算表达式列于表2-12。

对于常见截面的几何特征计算式列于表2-13。工程师应选择合理的断面形状以充分利用构件与结构的刚度。

表2-12 单跨梁内力与位移计算表达式

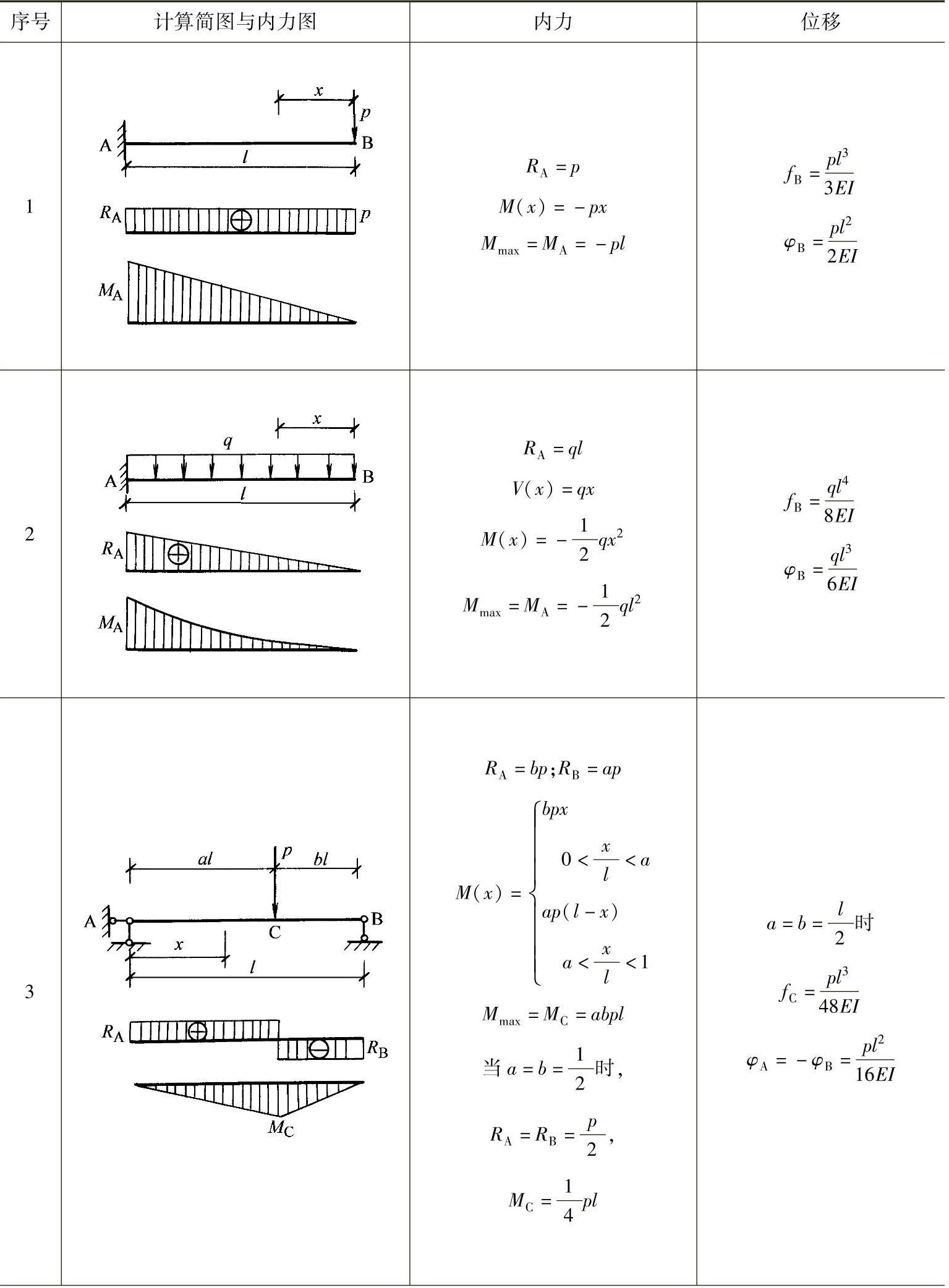
（续）

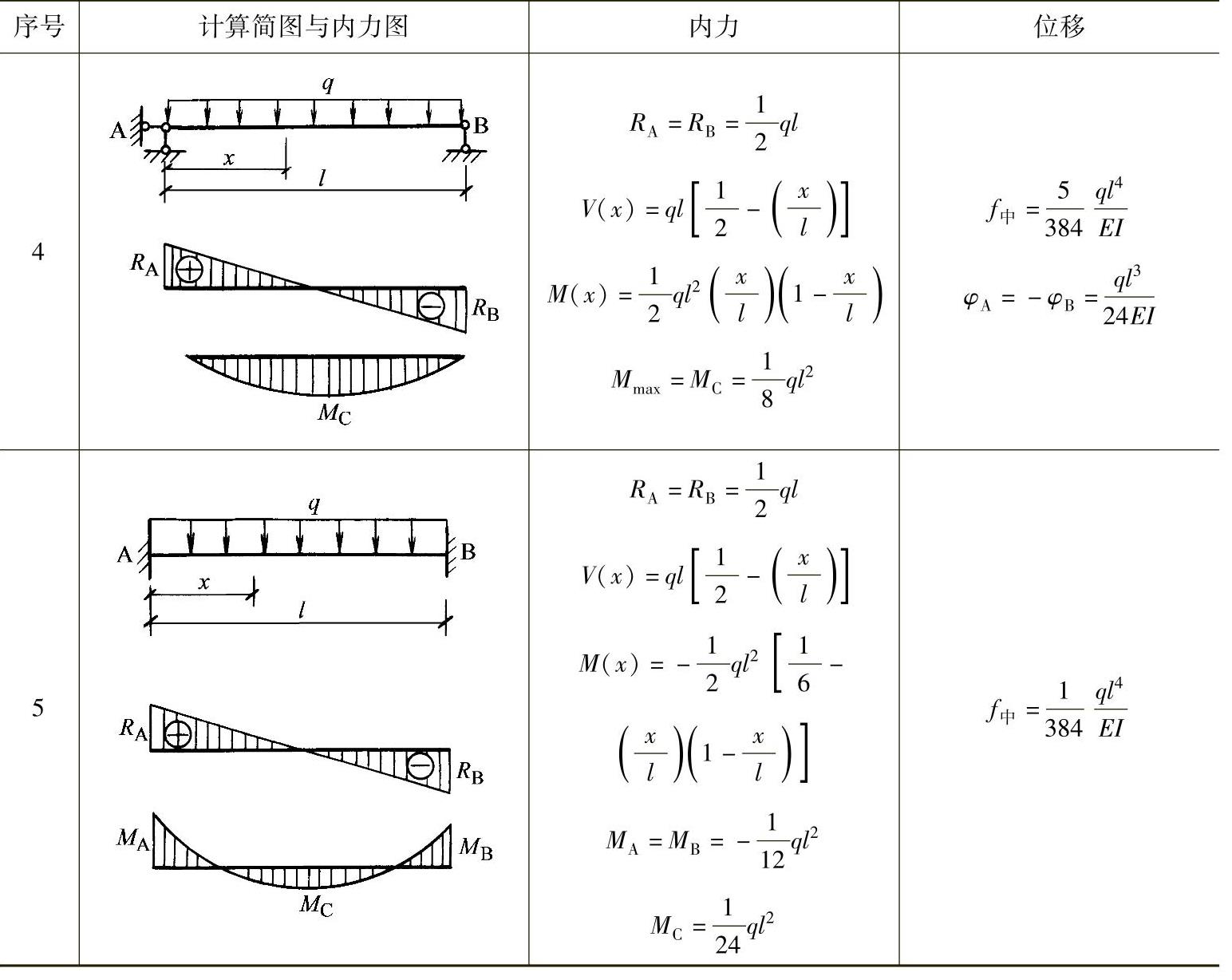
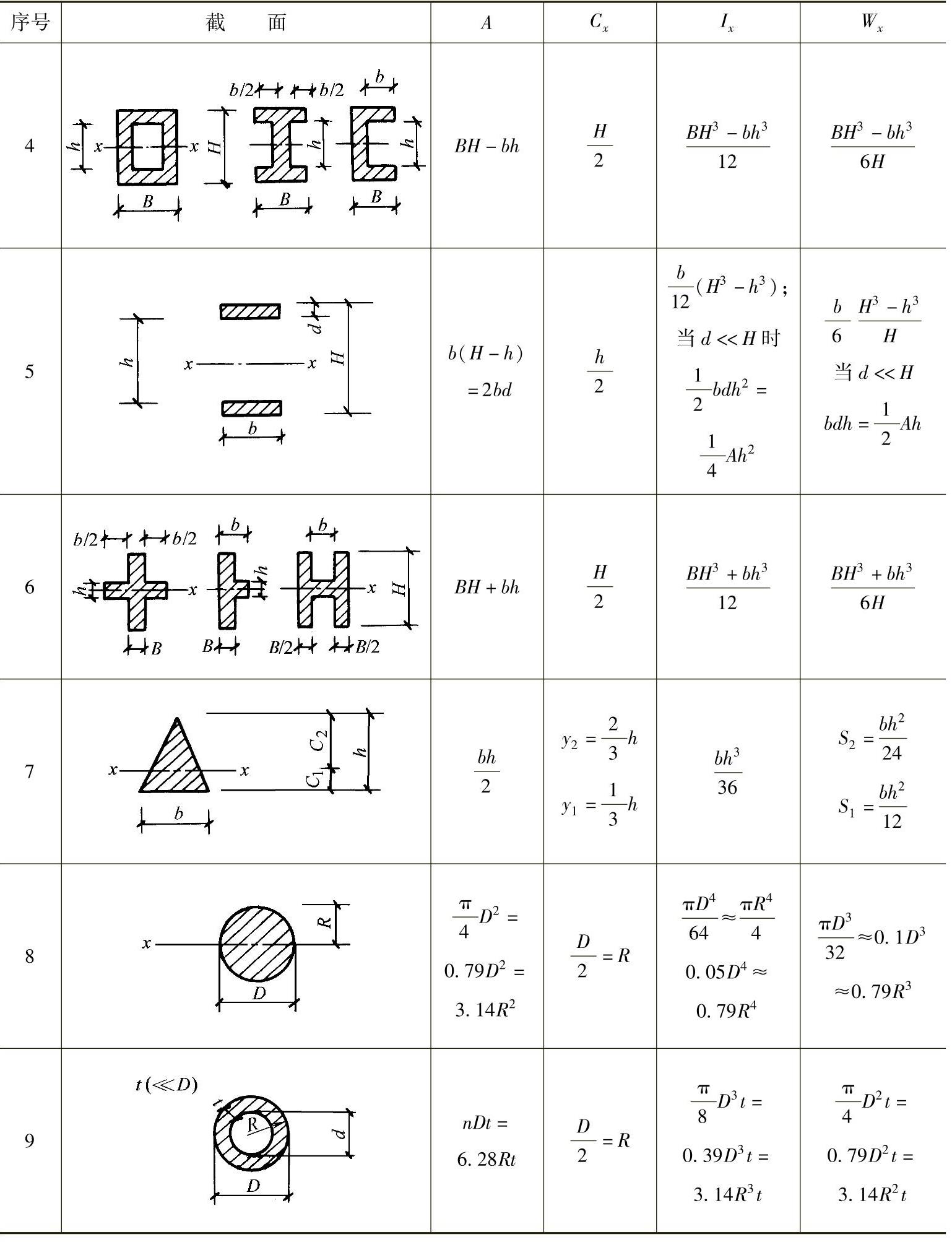
表2-13 常用截面的几何特征表

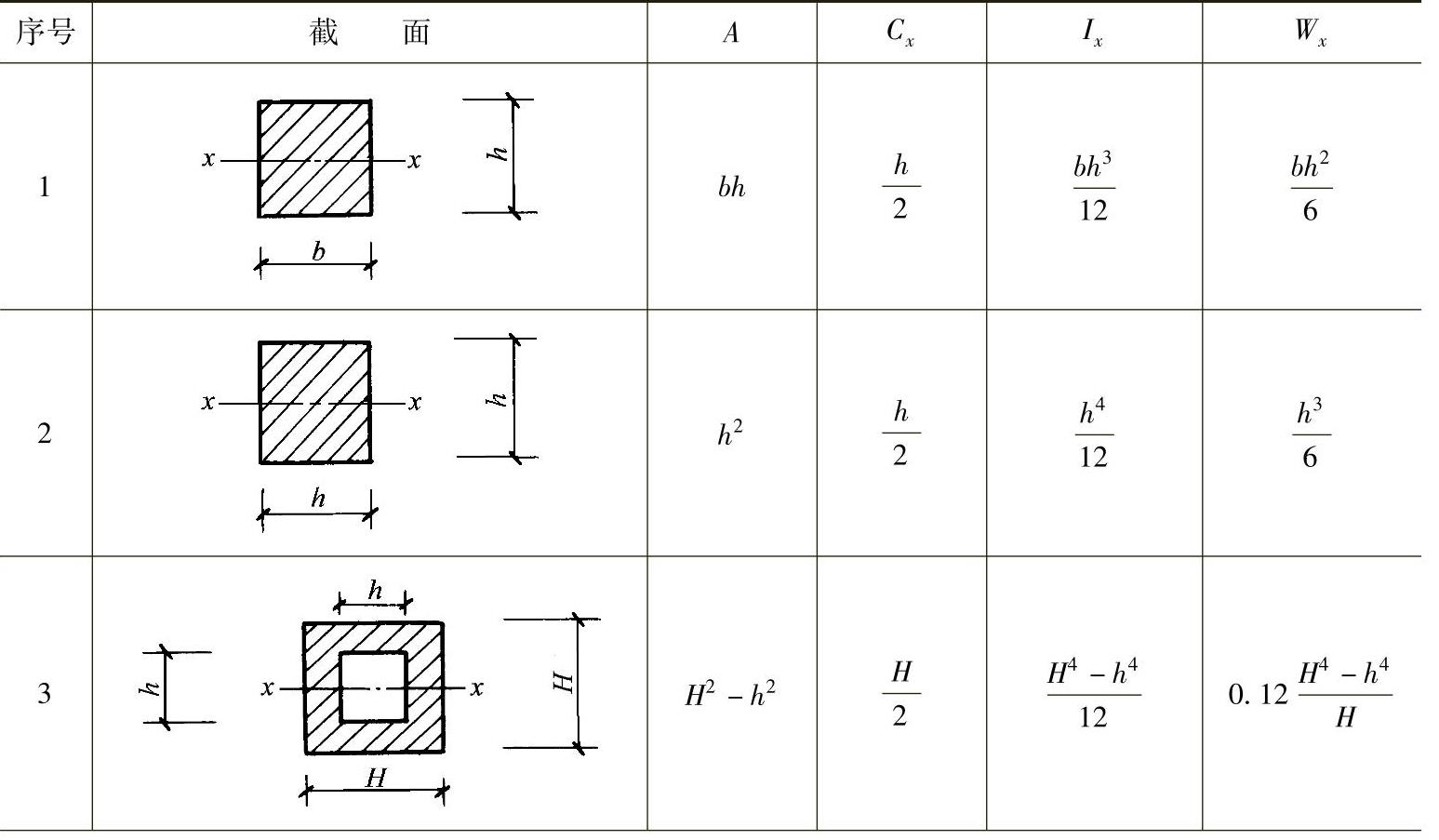
（续）

2.结构的变形设计和变形允许值

结构的变形设计，指的是结构受力后的变形必须满足正常使用极限状态的条件，即

f_max≤[f] （2-41）

式中 f_max——结构在荷载标准值作用下由弯矩算得的最大挠度或侧移；

[f]——设计规范对结构变形的限值，即允许变形（挠度或侧移）值。

[f]值规定如下（l为跨度，H为建筑物总高度，h为建筑物层间高度，（ ）中的限值适用于使用上对挠度有较高要求的构件。悬臂构件的允许挠度值按相应数值乘以系数2.0取用。）：

（1）钢筋混凝土屋盖、楼盖及楼梯构件

1）当l<7m时 允许挠度为l/200（l/250）

2）当7m≤l≤9m时 允许挠度为l/250（l/300）

3）当l>9m时 允许挠度为l/300（l/400）

（2）钢楼盖梁和工作平台梁

1）主梁 允许挠度为l/400

2）其他 梁允许挠度为l/250

（3）钢筋混凝土框架结构

1）建筑物顶点允许侧移为 H/300（地震）

H/500（风）

2）建筑物层间允许侧移为 h/250（地震）

h/400（风）

（4）钢筋混凝土墙结构

1）建筑物顶点允许侧移为 H/700（地震）

H/1000（风）

2）建筑物层间允许侧移为 h/600（地震）

h/800（风）

【例2-9】 单跨钢筋混凝土简支梁，跨度l=10m，截面为矩形，b×h=300mm×1000mm。采用C20混凝土，E_c=0.255×10⁵N/mm²，承受均布荷载（包括梁自重、构造层重力荷载及楼面使用活荷载），其标准值q=40kN/m=40N/mm，求该梁跨中最大挠度。（由于在使用情况下钢筋混凝土梁一般在其受拉一侧都有微细裂缝，而且需要考虑恒载的长期效应，这些因素都会使截面抗弯刚度有所降低。因此，在计算钢筋混凝土梁的挠度时，其截面抗弯刚度值可按（0.20～0.30）E_cI估算）

【解】

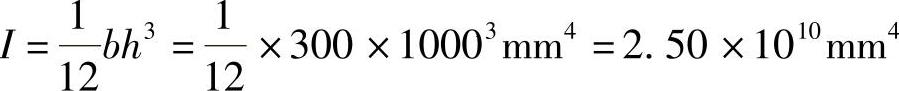
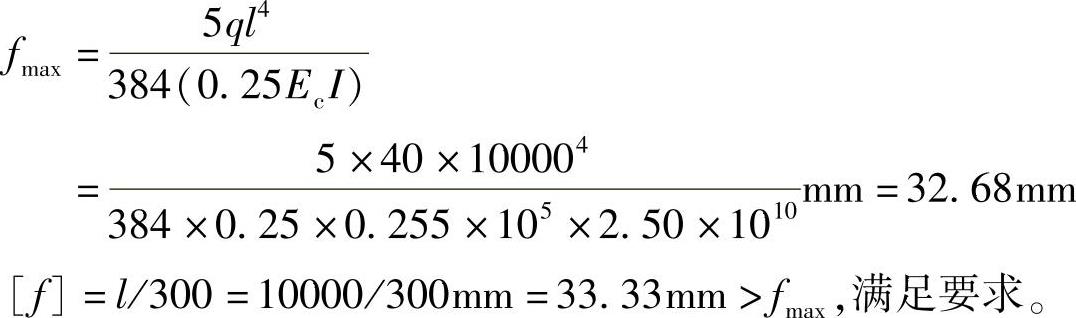
3.框架、剪力墙的侧移估算

多高层建筑常采用框架或框架—剪力墙结构，以抵抗侧向力。在框架—剪力墙体系中，框架主要承受竖向荷载，剪力墙主要承受水平荷载。钢筋混凝土剪力墙的侧移刚度比框架的侧移刚度大得多，往往抵抗了70%～90%的风荷载。整个结构体系的侧移量，主要由剪力墙来决定。因此，可以单计算剪力墙的侧移，来估算框架—剪力墙体系的侧移。不过剪力墙的侧移属弯曲型变形，由水平荷载产生的弯矩来确定，此时将剪力墙当作悬臂杆计算。框筒结构的侧移估算应是类似的，此筒体结构抵抗水平力和保证侧向稳定，更具有特殊的优越性能。

对于纯框架结构，则侧向变形以剪切变形为主，且高度通常不超过50m，可以忽略弯曲变形的影响，由侧向层间位移叠加求得总位移。

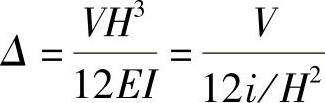
分母12i/H²为桩子抗切刚度，考虑到柱子非无限刚性，加上还有弯曲变形影响，计算时可取一修正系数

一般取α=0.3。

【例2-10】 图2-35所示为位于北京地区的某框架结构，6层，层高h=5m。总高H=30m，建筑物长20m、宽10m，柱截面尺寸bh=500mm×500mm，每层15个柱，采用C20混凝土，E_a=0.255×10⁵N/mm²，求风荷载作用下的框架顶端侧移和最大层间侧移。

【解】

（1）求风荷载

北京地区基本风压w₀=0.35kN/m²

风压高度变化系数取_μz=1.42（H=30m，大城市郊区）

风载体型系数_μs=+0.8（迎风面），-0.5（背风面）

沿建筑物高度的风荷载q=1.42×（0.8+0.5）×0.35×20kN/m

=12.92kN/m（假设沿高度均匀分布）

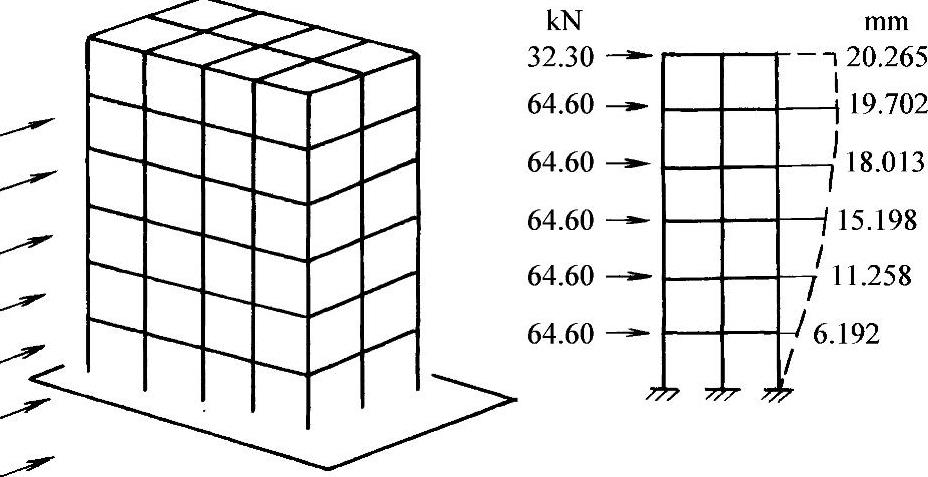
图2-35 【例2-10】计算简图

近似地以每层楼盖标高处承受集中风力F_w计，则

F_w=5×12.92kN=64.60kN

F_w/2=32.30kN

本例中建筑物总高30m，可不考虑风振系数β_z。

（2）确定[f]

计算框架顶点侧移时，[f]=H/500=30000/500mm=60mm

计算框架层间侧移时，[f]=h/400=5000/400mm=12.5mm

（3）用列表计算法计算框架每层侧移

框架的侧移基本上由每层柱子受剪切后发生弯曲形成的侧向变形积累而成。列表计算如下：

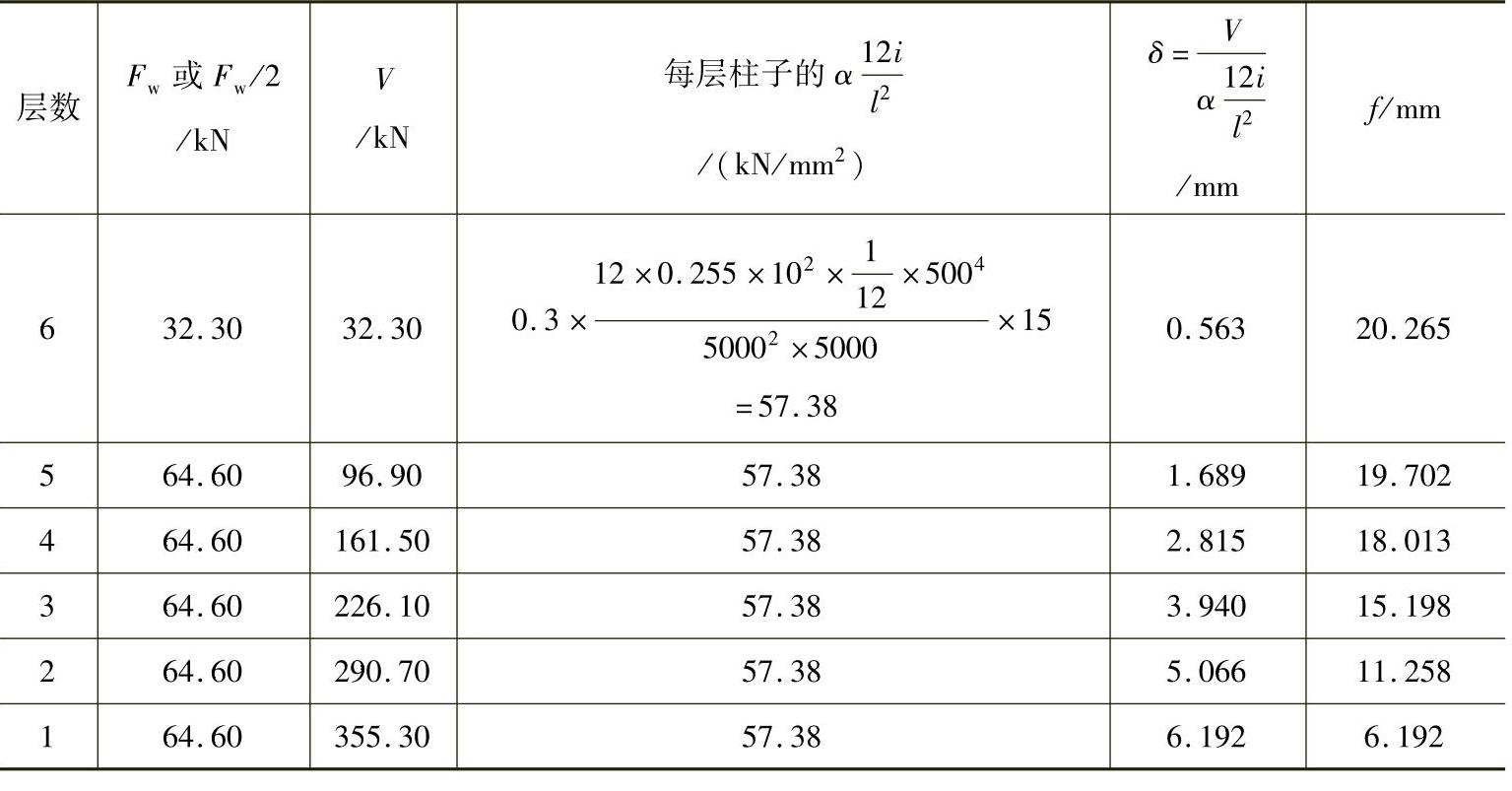
顶端侧移f_max=20.265mm<60mm

层间侧移f_max=6.192mm<12.5mm，均满足要求。

【例2-11】 一座层高h=3.6m的五榀框架，间距6m，每榀框架有4跨共13层。框架钢筋混凝土柱子平均截面尺寸为300mm×600mm，混凝土强度等级为C20。E=0.255×10⁵N/mm²，受风荷载1.5kN/m²。

试确定其顶点位移，又若此结构设置两堵剪力墙，墙宽6m，厚0.6m。即截面B×H=6m×0.6m，试求其顶点位移。

【解】

（1）对框架结构

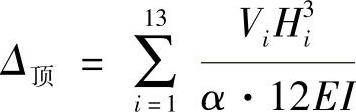
顶层集中风力： W=w·β·H/2

=1.5×6×3.6/2kN=16.2kN

其余各层风集中力W=w·β·H=2W_顶=32.4kN

顶层（13层）剪力 V₁₃=16.2kN

从上到下第二层（12层） V₁₂=48.6kN=3V₁₃

类推11层剪力 V₁₁=48.6+32.4=5V₁₃

各层抗剪刚度（考虑到四跨有5根柱及折减系数为0.3）为

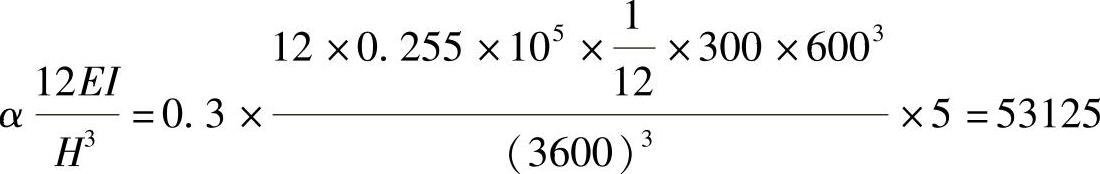
顶点位移为

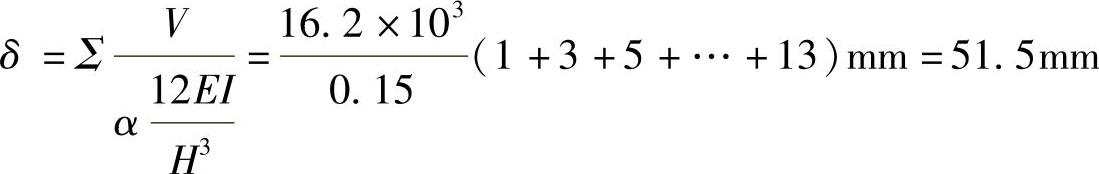
（2）建筑物宽4×6m=24m。建筑物所受风荷载（沿高度每延米长的风荷载）为：

1.5×24kN/m=36kN/m

有两片剪力墙，设剪力墙承受80%的侧向荷载，每片剪力墙各分担1/2，即：

W=36×0.8×0.5kN/m=14.4kN/m

把剪力墙看做嵌固于刚性基础的悬臂梁，则其顶端位移为：

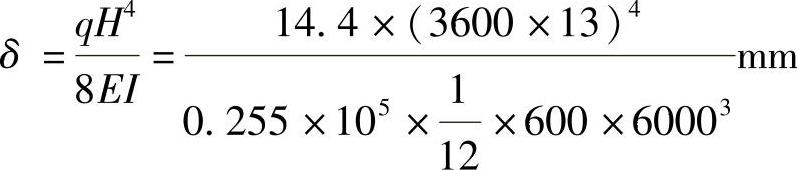
=31.35mm

【例2-12】 图2-36所示为一幢13层办公楼，在建筑物中心设有一个6m×12m的电梯井，井筒外侧有18根外柱。屋盖和楼层的恒载是6kN/m²，墙面所受的水平风荷载是1.4kN/m²，井筒墙的恒载是5kN/m²，井筒壁厚为300mm，预应力钢筋混凝土框架由300mm×750mm的T形梁和边长为500mm正方形钢筋混凝土柱组成，试验算建筑物的抗倾覆能力并计算建筑物顶部的侧移。

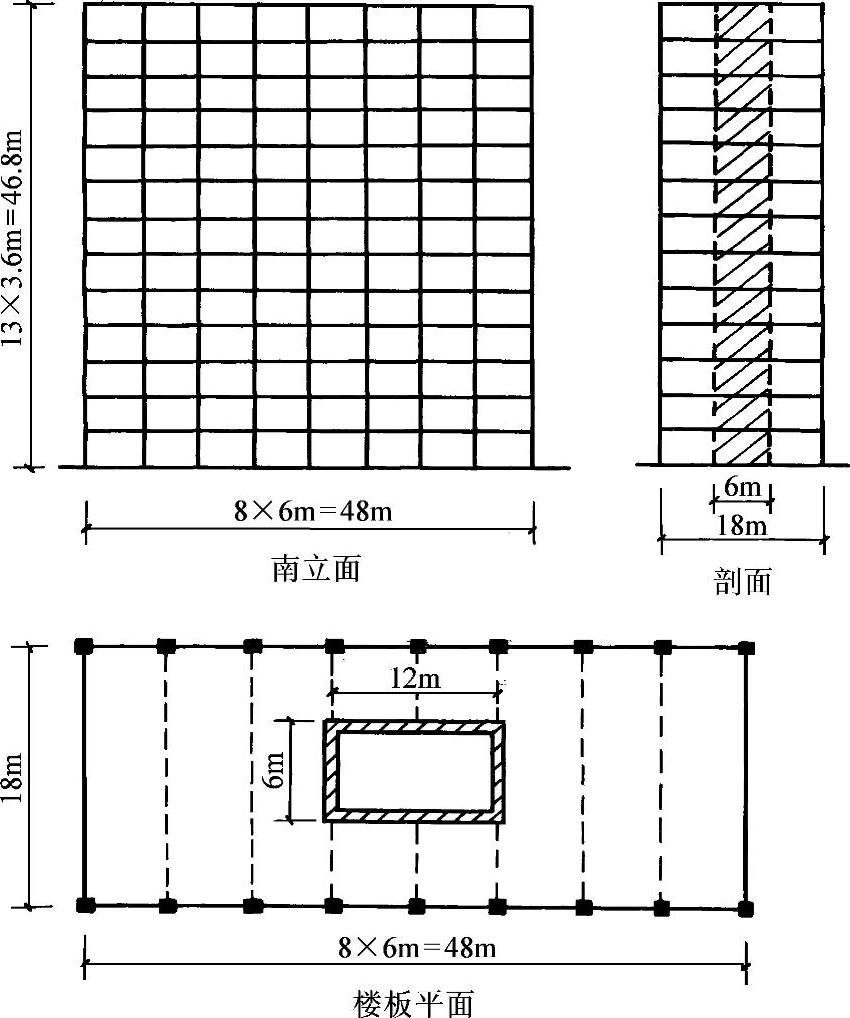
图2-36 【例2-12】计算简图

【解】

（1）抗倾覆验算

地面以上13层楼板总重G等于屋盖和12层楼盖恒载的总和

G=6×18×48×13=67392（kN）

井筒负担竖向荷载的面积为18m×12m=216m²，是总面积48m×18m=864m²的1/4，因此核心筒承担的荷载为(www.daowen.com)

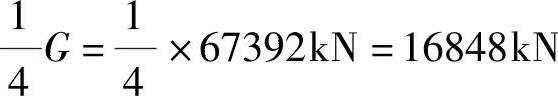
再考虑井筒墙的恒重5kN/m²，则抗倾覆的总重量

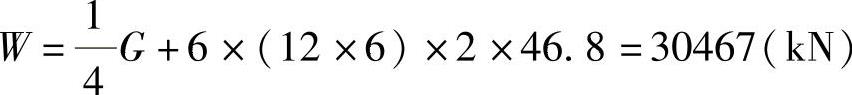
抗倾覆力矩

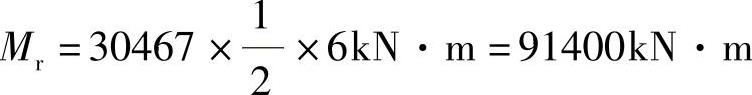
倾覆力矩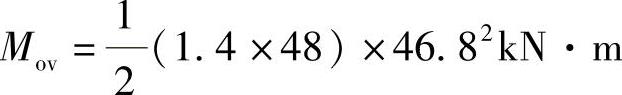

=73592.1kN·m<M_r（安全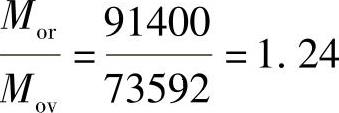）比1.5小一点，安全系数不太够。考虑到基础宽度较大，故判断建筑物不会倾覆。

（2）建筑物顶端侧移估算井筒截面外壁尺寸为

（12+0.3）m×（6+0.3）m=12.3m×6.3m

井筒内壁尺寸为

（12-0.3）m×（6+0.3）m=11.7m×5.7m

惯性矩为

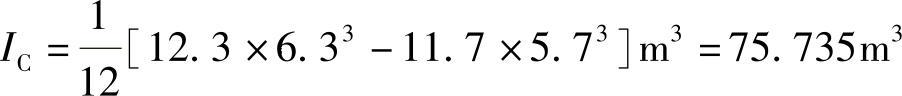
q=1.4×48kN/m=67.2kN/m

设混凝土的强度等级是C20，则弹性模量为

E_C=0.255×10⁵N/mm2

故悬臂结构顶点侧移

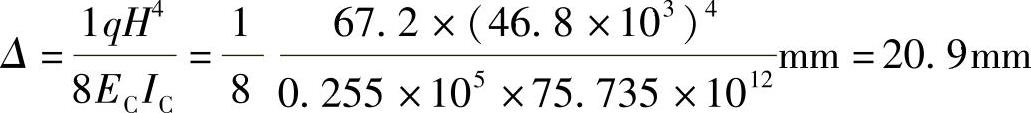
【例2-13】 对世界贸易中心大楼进行抗倾覆和位移估算。

世界贸易中心（The World Trade Center）是世界著名高楼，在2001年的“9.11”事件中被撞毁。原建筑是110层的方形塔楼，高412m，平面尺寸63.5m×63.5m，采用筒中筒结构，外筒为密柱框筒。底层每边有19根箱形截面的钢柱，柱距3.05m，箱形柱的截面尺寸为686mm×813mm，壁厚平均为90mm，柱截面面积A_c=0.263m²，角柱适当加强，如图2-37所示。世界贸易中心总体高宽比H/d=412/63.5=6.49，大楼位于大西洋海边，30m以上风荷载为2.692kN/m²，平均风荷载为2.5kN/m²，现估算仅考虑水平风荷载时，该建筑总体的高宽比是否满足抗倾覆要求。

【解】

（1）将问题简化

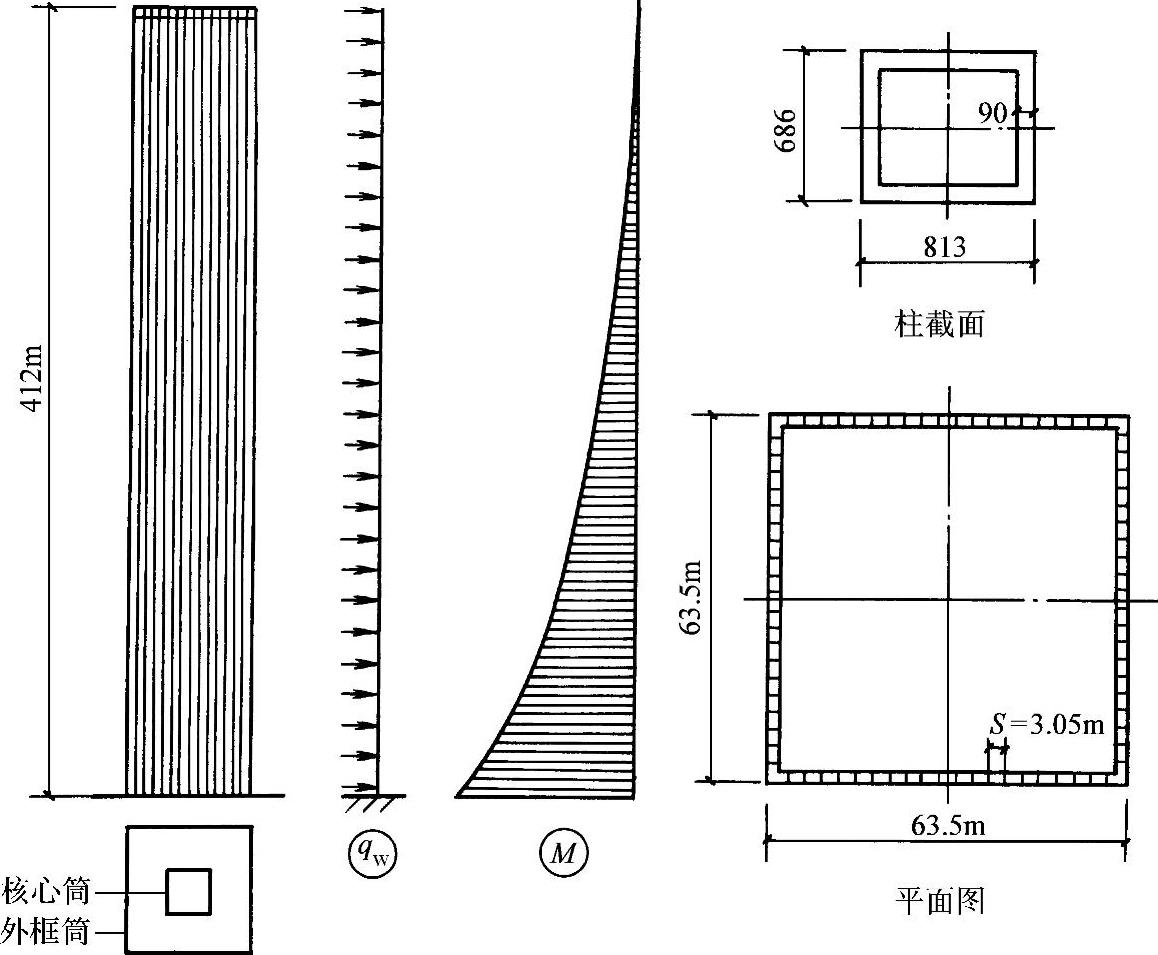
图2-37 【例2-13】世界贸易中心估算简图

1）把世界贸易中心塔楼看做嵌固在地面上的悬臂梁。

2）抗倾覆估算主要考虑水平荷载的作用，由于内筒作用与外筒作用相比较小，因此估算时，仅考虑外框筒的作用。

3）外框为密柱形成外筒，近似看做共同工作的箱形截面；不考虑轴向变形的影响。

4）角柱仅有4根，近似与中柱一样对待，风荷载取平均值，沿高度均布。

（2）水平荷载的倾覆力矩M_r及抗倾覆力矩M_ov的估算

1）倾覆力矩M_ov=FηH：

F=q_wBH=2.5×412×63.5=65405（kN）

η=1/2

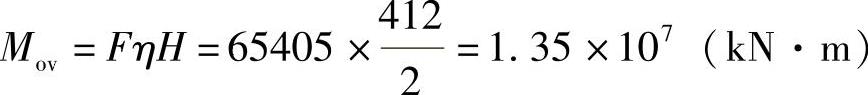
2）抗倾覆力矩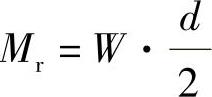

W=6×63.5×63.5×110=2661285（kN）

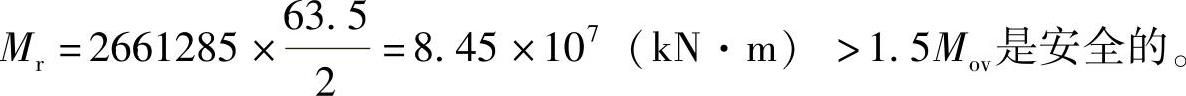
（3）建筑物位移估算

1）房屋结构底层总弯矩

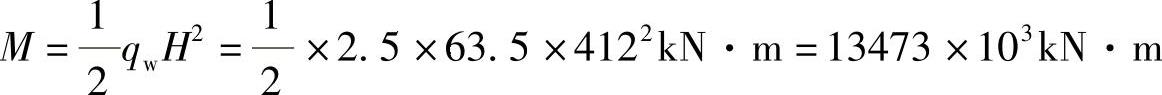
2）房屋结构总体截面惯性矩I

为简化计算，沿风荷方向的框筒柱近似按“拍扁”后的等效“腹板”计算，则“腹板”的等效厚度

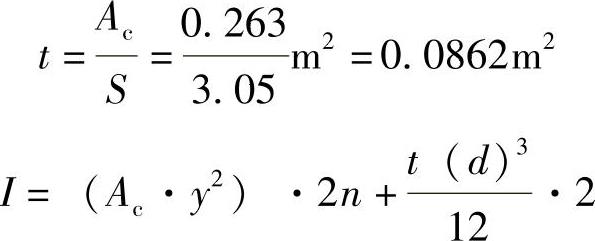
式中 A_c——柱截面面积；

S——柱间距；

n——每边的柱数；

y——框筒柱离截面中心的距离；

d——结构总宽度。

则房屋结构的总体截面惯性矩

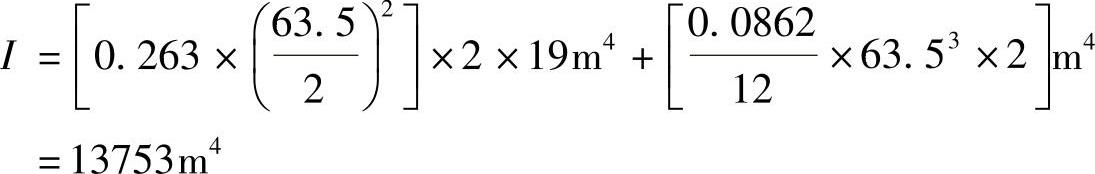
边柱由风荷载引起的最大附加应力为

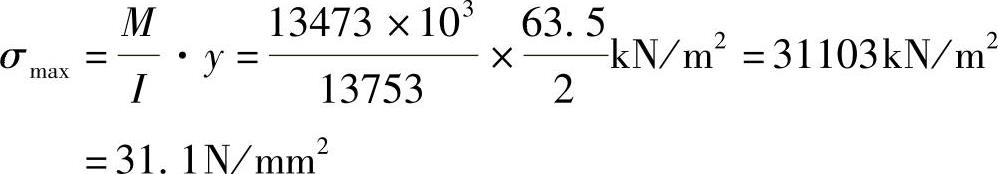
即风荷引起的柱内最大附加应力为

σω=31.1N/mm²

单柱由风荷引起的附加内力为

Nω=A_cσ_max=0.263×31103kN=8180kN

3）风荷作用下房屋顶端侧移估算

等截面悬臂梁端点挠度计算公式为Δ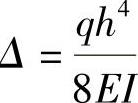，世界贸易中心框筒的箱形截面柱是变截面柱，底部柱截面面积为A_c，越往上截面越小，可近似认为是柱顶截面为0的均匀变截面构件，则变形要比等截面构件大些，此时的顶端侧移为

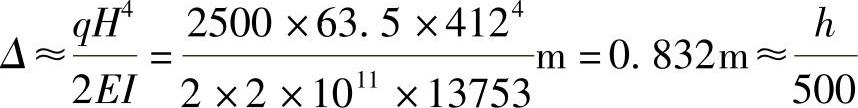
按美国规范，允许侧移为

[Δ]=0.002h=0.002×412m=0.824m≈Δ

考虑到内筒等作用，可以认为满足设计要求

4.结构平面中构件截面布置对刚度的影响

下面我们讨论一座小塔楼的几种结构方案，研讨如何提高结构的刚度。设塔楼平面尺寸相同，边长均为5.2m，结构截面面积均为4m²。

方案1：由4根1m见方小柱组成，其截面刚度为4根柱截面刚度的总和

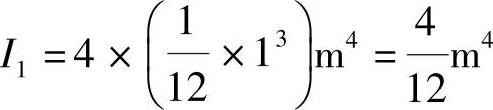
方案2：若将4根小柱合并为1根大柱，则刚度为

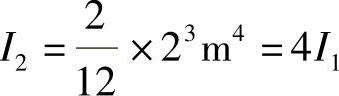
方案3：若将4根1m见方的柱“拍扁”，做成4片独立的墙，每片为0.2m×5m。由于墙体出平面的刚度很小，而平面内的刚度比出平面刚度要大得多，在水平荷载作用下，垂直荷载方向墙的刚度可以忽略不计，荷载仅由沿着荷载方向的两片墙来承受，故其刚度为

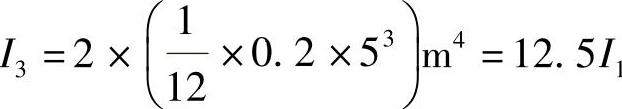
方案4：若将上述四片墙在墙角处连成整体，形成箱形截面，根据材料力学知识

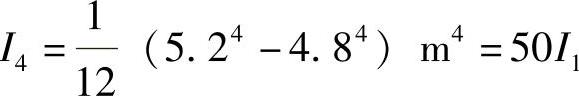
比较以上几种结构方案可以看出，尽管截面面积相同（即使用相同数量的建筑材料），但通过合理改变结构形式，则可以大大提高刚度。

由以上分析对比可见：

1）将小柱合并成大柱，可有效地提高抗侧移刚度，这是结构设计中所谓材料集中使用的原则。

2）结构墙的平面内刚度要比柱大得多，利用结构墙可大大提高房屋的抗侧移刚度。

3）垂直荷载方向的墙体在独立工作时处于出平面受弯状态，其抗弯刚度与平面内抗弯刚度相比小得可以忽略不计。然而，当组成整体箱形截面后，它是作为箱形截面的“翼缘”参加抗弯工作，内力臂很大，是箱形截面抗弯刚度的主要部分，从而可大大提高其抗弯刚度。

4）对比方案3和方案4，刚度相差4倍，而实际上差别仅在于将四片独立墙连系起来，使其整体共同工作，形成一个完整的箱形截面（即筒体），截面变形符合平面假定。由此也可以看出墙片间连接构造的重要性，如果连接失效，方案4又会恢复为方案3，抗弯刚度下降到四分之一。

由此推理，若能将方案1的4根柱加上刚性联系，使其共同工作，截面变形符合平面假定，则刚度还可提高。上述方案都只是在结构平面上的改进，其实还可在立面上想想办法。

方案5：如图2-38所示，若在4根小柱顶端加上刚性很大的连系梁，形成框架，保证4根小柱像整体截面一样共同工作，成为方案5，则其抗弯刚度为

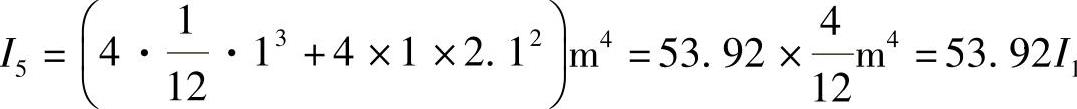
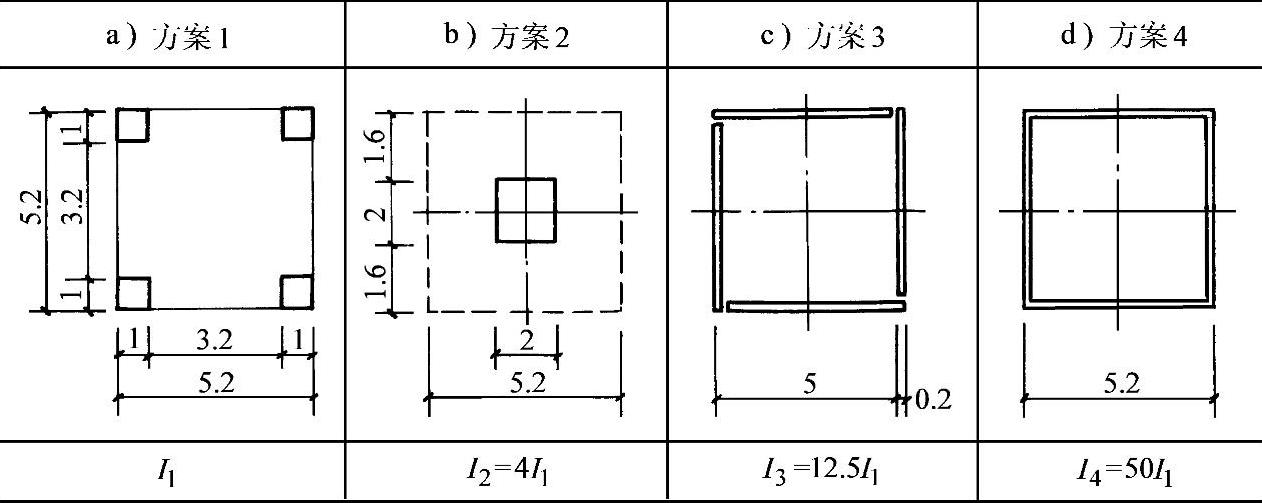
图2-38 结构截面刚度的比较

方案5刚度要比方案4还大。我们来分析一下方案5的受力状态，例如在左侧水平荷载下，若没有刚性横梁，则两排柱都将像独立悬臂柱一样自由侧移。若在柱顶加上“刚性”横梁，刚性横梁与柱刚性连接，刚性横梁在柱变形前与柱垂直相交，在柱变形后仍要保持与柱垂直相交，为此，刚性横梁中存在很大剪力，迫使左柱拉长、右柱压缩。在柱中产生轴力V，左柱受拉、右柱受压，形成反向力矩V·d，抵消了一部分倾覆力矩。若以柱顶刚性横梁作脱离体，刚性横梁受到左柱拉力和右柱压力的力矩作用，转角大大减小。可见，柱间刚性横梁使柱顶变形一致，引起柱内附加轴力，并组成反向力矩，大大减少了柱顶侧移，提高了结构刚度。有关刚性横梁的作用在后面结构竖向体系分析中还要详细讨论。

方案5实际上是一榀带刚性横梁的单层框架，单层框架的抗侧移刚度比独立柱好得多。但若柱子过长过高，受压过程中容易失稳。为此，我们可以增设中间横梁，形成多层框架，以减少柱子的计算长度，防止柱子失稳。或者分层后，中间加上交叉支撑，则可大大增加抗侧刚度。

5.绘制结构弯曲变形的示意图

在工程的方案设计阶段，设计人员往往要判断结构构件哪一面受拉、哪一面受压，以便估计钢筋放在构件的哪一侧，有时更要定性地估计结构受力后的挠度和侧移情况。为此，懂得一些绘制结构构件受力后的弯曲变形示意图的规律是很有用的。

一般说来，结构构件受力后的弯曲变形图有以下几点规律：

（1）由于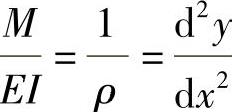，人们就可以根据弯矩图直接画出构件的弯曲变形示意图。在弯矩图无突变的情况下，弯曲变形图为一连续曲线，不存在转折。其中：

M值大的区段，曲率半径ρ小，变形曲线的曲率大；

M值小的区段，曲率半径ρ大，变形曲线的曲率小；

M=0的区段，曲率半径ρ等于∝，变形曲线为直线；

+M值的区段，变形曲线为凹形；-M值的区段，变形曲线为凸形。显然，外鼓的一侧受拉，内凹的一侧受压。以上规律可参看图2-40。

（2）对于一端为固定端的悬臂梁或下端为固定端的悬臂柱，无论在与构件长度方向相垂直的集中荷载作用下还是在均布荷载作用下，变形曲线均凸向荷载作用方向，固定端处的曲线与原构件轴线相切，如图2-39a所示。推而广之，凡固定端支承点处，变形曲线的切线必定与固定端面相垂直。

（3）凡连续不动铰支承点处，两侧变形曲线的切线斜率不变，如图2-39b所示。

（4）凡不动铰支承点和固定端支承点处，在水平和竖直方向上均不得有任何位移；而滚动支承点处在沿滚动方向上可以有微小位移，如图2-39c所示。

（5）凡刚节点处，与该节点连接的杆件可以任意转动，但它们之间的夹角不变（图2-39d）；刚节点在荷载或其他作用力作用下，可能有位移，也可能没有。

（6）凡铰结点处，与该节点连接的杆件的夹角可以作任意变化，但由铰节点引出的变形曲线段为直线（图2-39e）；铰节点在荷载或其他作用力作用下，可能有位移，也可能没有。

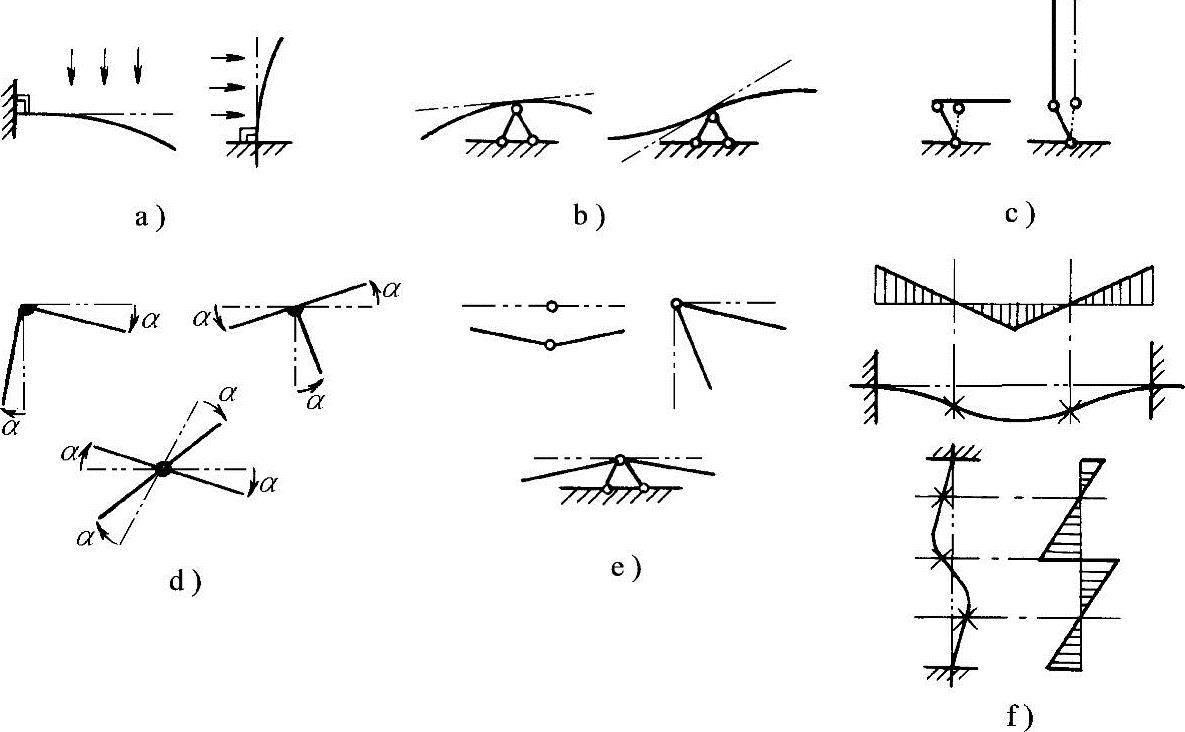
1图2-39 弯曲变形一般规律

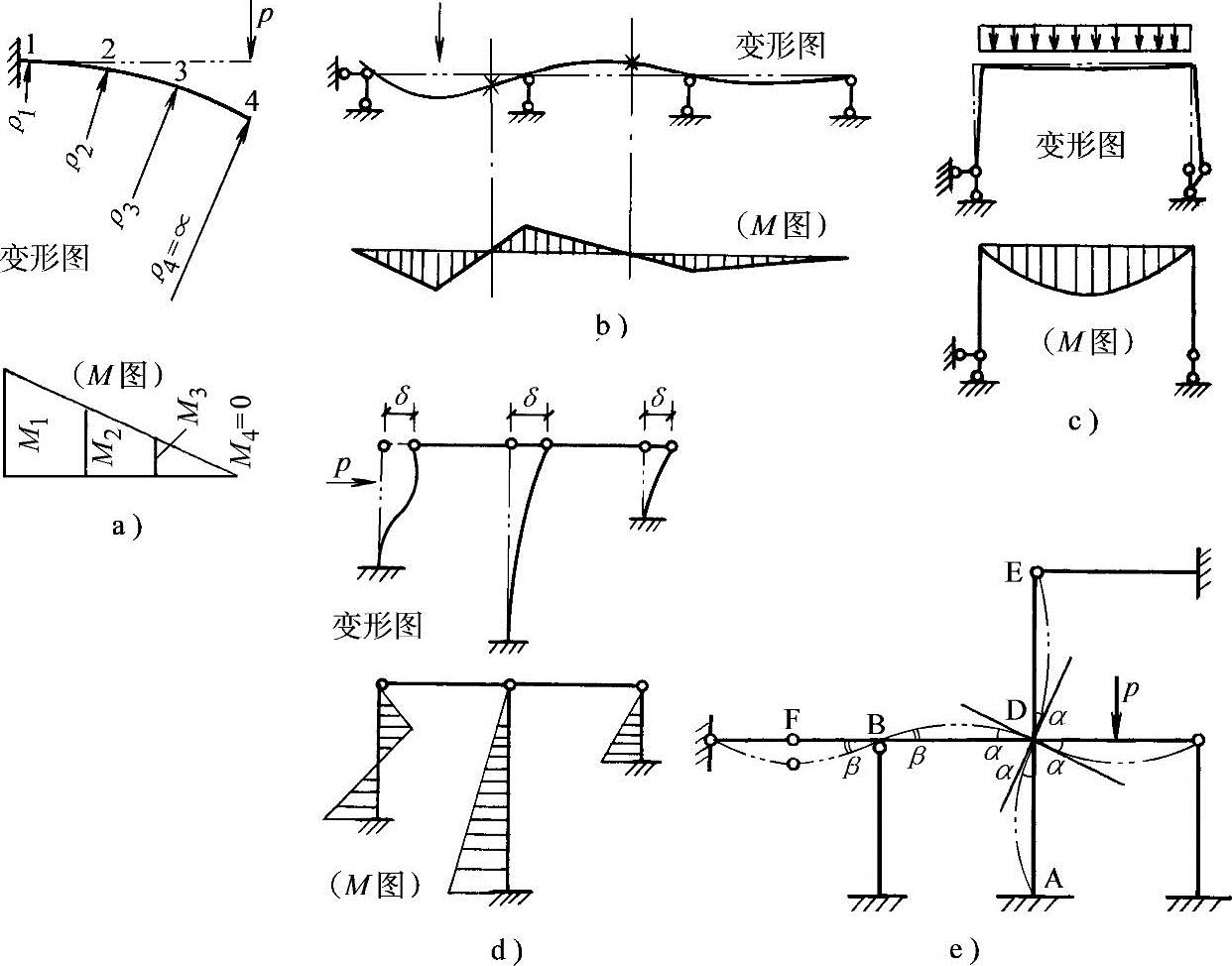
图2-40 弯曲变形示意图

a）悬臂梁 b）连续梁 c）单跨刚架 d）两跨排架 e）两层两跨排架

（7）凡反弯点处（M=0），在变形曲线上为一拐点，连接拐点的变形曲线为一连续曲线；反弯点在荷载或其他作用力作用下有位移，如图2-39f所示。

（8）绘制弯曲变形示意图时，一般不考虑轴向变形，因而杆件的长度可以认为是不变的。

绘制弯曲变形示意图步骤如下：

1）画出构件在荷载或其他作用力作用下的弯矩示意图；

2）根据弯矩示意图和上述规律作变形示意图；作图时，一般从直接受载的构件画起，按顺序对与它连接的构件作图，最后画到支承处；

3）按照弯曲变形图的规律，对照弯矩示意图进行全面检查。

图2-40举例表示悬臂梁、连续梁、单跨刚架、两跨排架、两层两跨框架在荷载作用下的弯曲变形示意图。