多层框架结构在竖向荷载和水平荷载作用下的近似受力分析,可分别采用建筑力学中的分层计算法和反弯点计算法或铰点法计算。
1.分层计算法
分层计算法的要点是:①把多层框架(图2-26a)分解为若干个分层框架,每个分层框架由各层的梁和与其上下毗连的柱组成,柱的远端看成固定端支座(图2-26b);②分别用建筑力学中的力矩分配法计算各分层框架;由图2-26b可见,每根柱同属于相邻的两个分层框架,因此,柱的最后弯矩应由两部分叠加得到;③在各分层框架中,应将上层各柱的线刚度乘以折减系数0.9;传递时,凡远端实际不是固定端的柱,传递系数由1/2改为1/3(注意:底层柱不作如上修改);④分层计算的结果组合在一起,便得到框架结构整体的弯矩图。
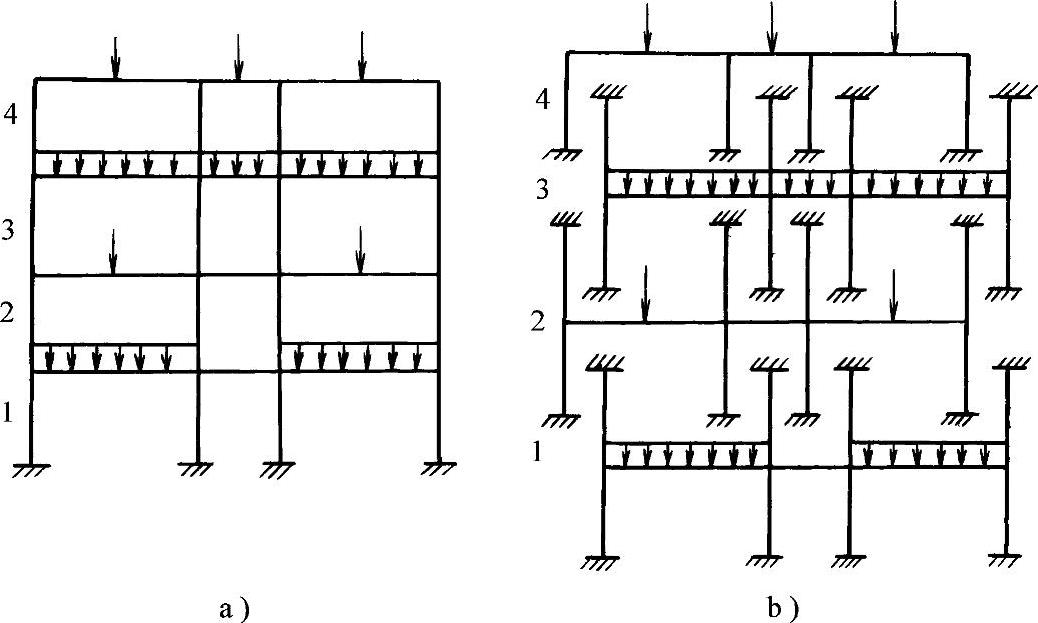
图2-26 分层法示意图
a)框架结构计算简图 b)分层框架计算简图
2.反弯点法
反弯点计算法的要点是:①假设框架结构横梁的相对刚度为无限大,因而框架节点在水平节点荷载作用下不能产生转角,只发生侧移;②在框架同层各柱端有同样侧移时,同层各柱的剪力与柱的侧移刚度成正比;每层柱共同承受该层以上的水平节点荷载;各层的总剪力按各柱的剪力分配系数分配到各柱;③上层各柱在水平节点荷载作用下的反弯点设在柱中点,底层柱的反弯点设在柱子的2/3高度处;④柱端弯矩根据柱的剪力和反弯点位置确定;梁端弯矩由节点力矩平衡条件确定;中间节点两侧的梁端弯矩按梁的转动刚度分配不平衡力矩求得。反弯点法计算示意见图2-27。
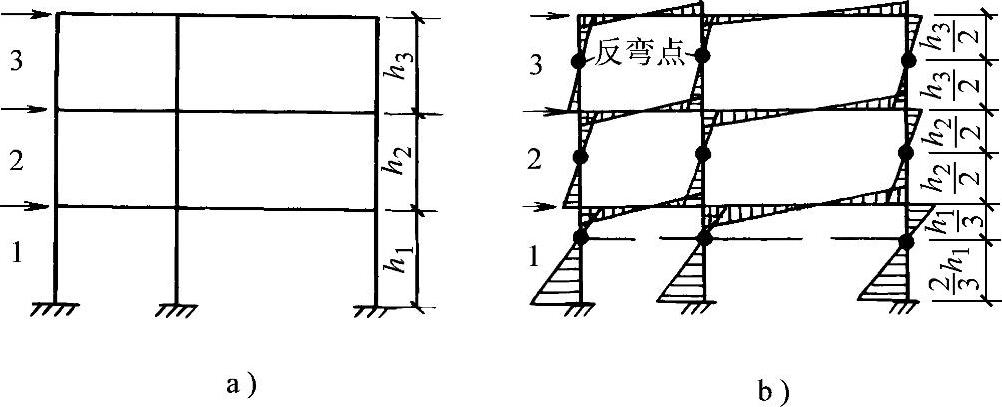
图2-27 反弯点法示意
a)水平节点荷载 b)反弯点及弯矩图示意
3.铰点法
无论分层还是多层,竖向荷载还是侧向荷载均可用“铰点法”分析。反弯点法实际上是将柱中设置铰的分析方法。在竖向荷载作用下的估算中,也可借用反弯点法的思路,在横梁上选定铰点(弯矩为零的虚设铰),再利用单梁法计算内力。一般可以假设在离梁端点0.2l处形成铰点,中间铰则为(1-2×0.2)l=0.6l(图2-28a),于是最大的正、负弯矩(如图2-28b)为
跨中正弯矩: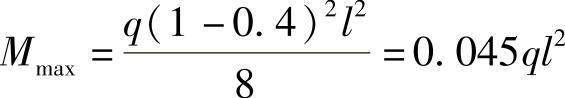
节点梁负弯矩:
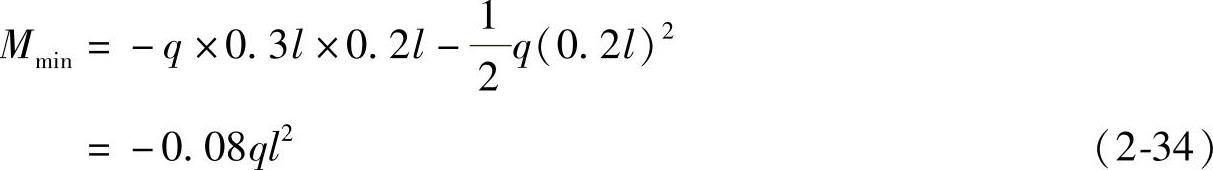
这些值与固端梁的0.042ql2和-0.084ql2很接近。柱端的弯矩可由节点平衡条件计算。对于内柱,只要应力保持低值,比如说为容许应力的70%~80%,则可认为不受弯矩作用,按中压柱计算。
对于边跨,可以假定铰点在距外柱0.1l处和距内柱0.2l处(图2-28b),而其弯矩为
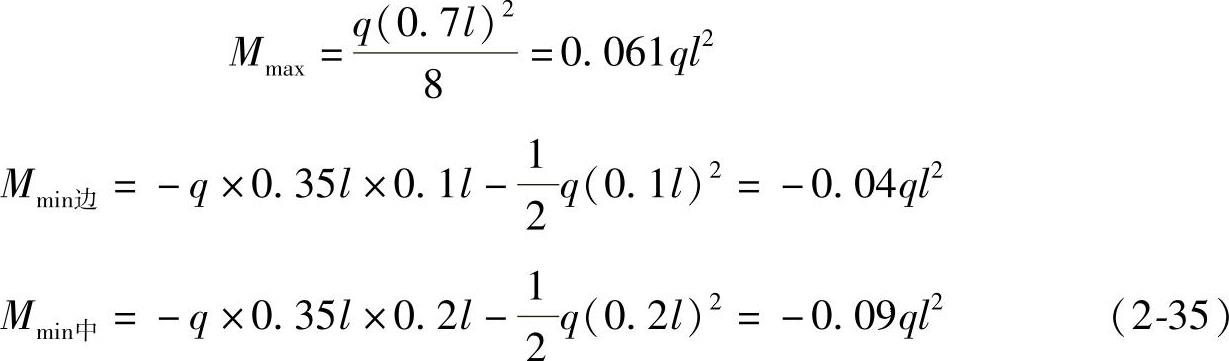
这些值应该与一端为固定、另一端为简支的梁的0.07ql2和-0.125ql2比较接近。
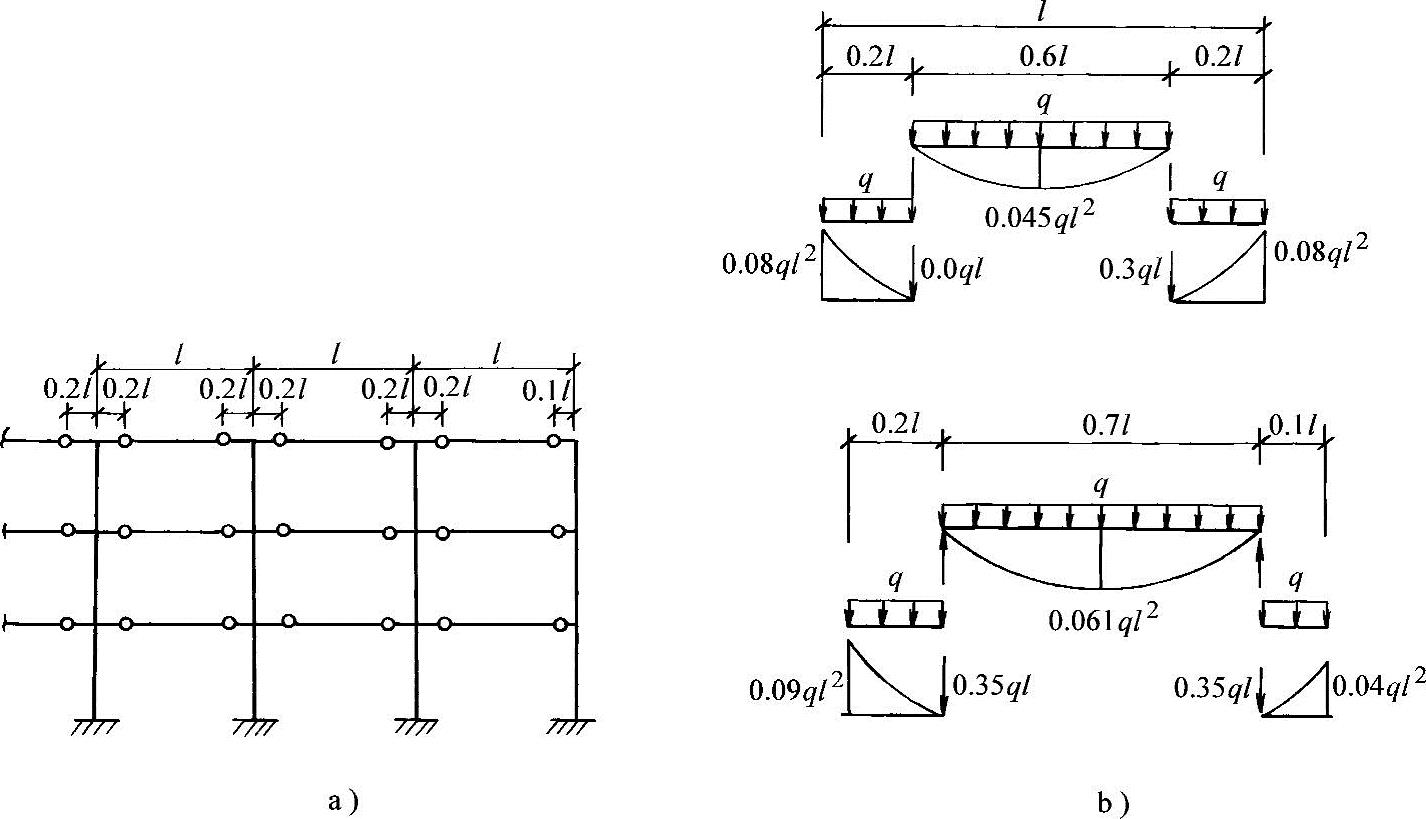
图2-28 铰点法计算简图
【例2-6】 试确定图2-29中,在竖向荷载作用下框架的弯矩。设此框架是一组中到中为6m的框架之一,其总均布荷载为11.5kN/m2。
【解】 以顶层为例,横梁中设“虚铰”,边跨靠边为0.1l,中间为0.2l则由式(2-35)得:
ql2MN=11.5×6×(7.2)2kN·m
=3577kN·m
ql2NP=11.5×6×(5.4)2kN·m
=2012kN·m
MMN=MMJ=-0.040×3577kN·m
=-143.1kN·m
MPN=MPL=-0.040×2012kN·m=-80.4kN·m
MNM=-0.09×3577kN·m=-322kN·m
MNP=-0.09×2012kN·m=-181kN·m(https://www.daowen.com)
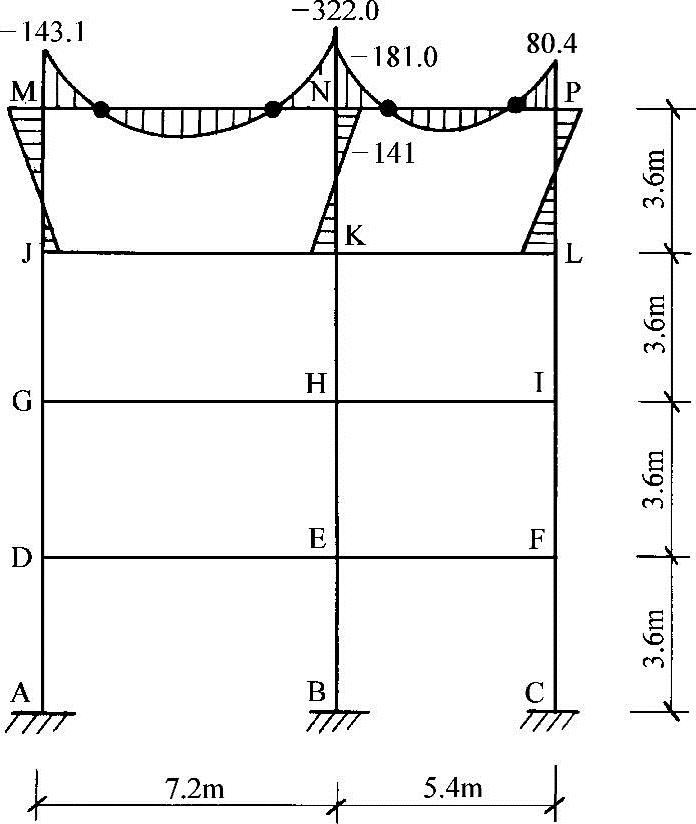
图2-29 【例2-6】计算简图
内柱的弯矩,可以假设在顶层为相邻两梁的弯矩之差,而对于标准层则为相邻两梁的弯矩之差的一半,故
MNK=MNM-MNP=(-322+181)kN·m=-141kN·m
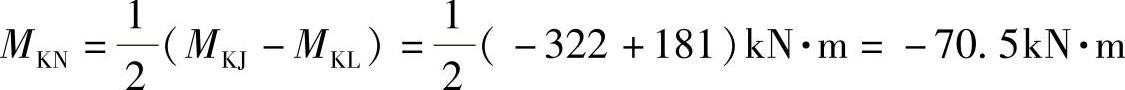
此处梁的弯矩符号是下拉为正,上拉为负。
梁MN跨中弯矩
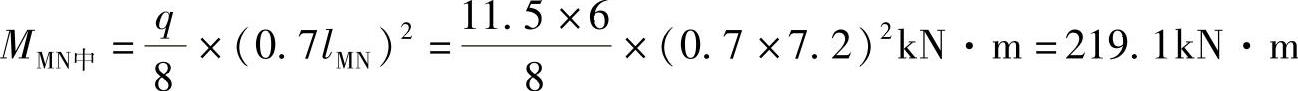
梁NP跨中弯矩
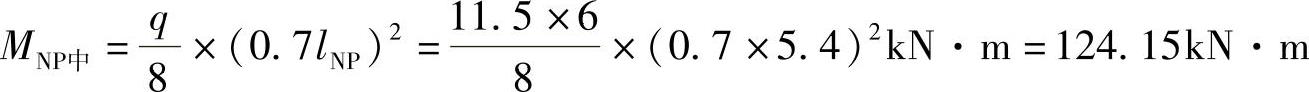
【例2-7】 图2-30所示为5m开间的四层单跨框架结构,跨度为10m,层高为5m,恒载总重9.0kN/m2(其中楼盖恒载重5.0kN/m2,墙柱折合4.0kN/m2,楼面活荷载2.0kN/m2,按7度抗震设防。梁柱线刚度比为2.33,估算地震荷载并用反弯点法绘M图。
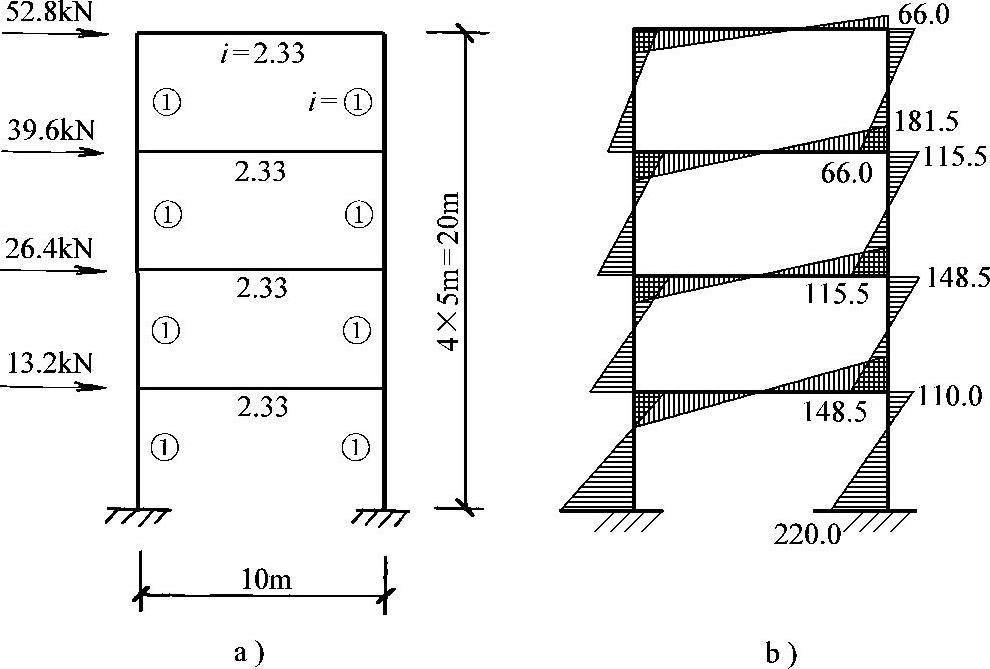
图2-30 【例2-7】计算简图
【解】
(1)荷载(标准值)
每层梁上所承受的均布荷载为
5×(5.0+2.0)kN/m=35.0kN/m
每一开间建筑物每层总重
5×10×(9.0+2.0)kN=550.0kN
四层总重
Geq=4×550.0kN=2200.0kN
每一开间总水平地震作用
FE=0.06Geq=132.0kN
按倒三角形分布则第四、三、二、首层楼盖标高处的水平地震作用分别为52.80kN、39.60kN、26.40kN、13.20kN,标注于图2-30上。
(2)反弯点法计算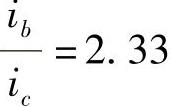 ,接近于3,用反弯点法能得到较好的精度。处理为对称框架,则
,接近于3,用反弯点法能得到较好的精度。处理为对称框架,则
每层柱的剪力分配系数都为0.5。除底层反弯点在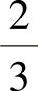 h处外,以上各柱反弯点都取在柱中点。柱端弯矩:
h处外,以上各柱反弯点都取在柱中点。柱端弯矩:
顶层: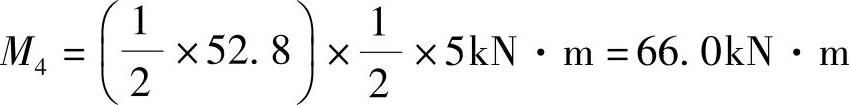
三层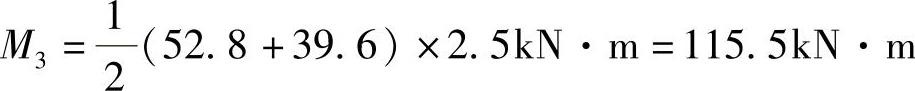
二层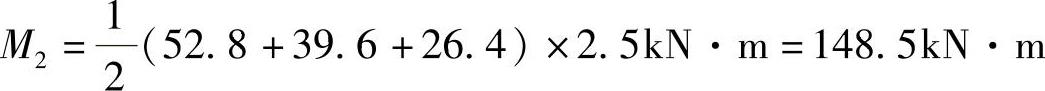
底层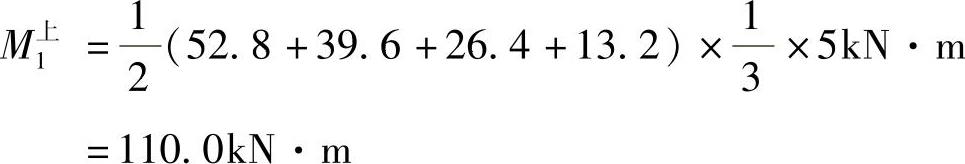
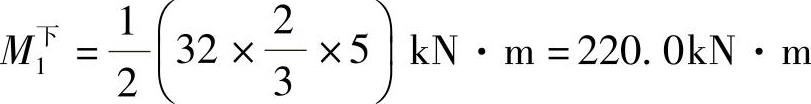
按节点力矩平衡条件,可以求得各梁端的弯矩:顶层梁端弯矩直接与柱端弯矩相等,三、二、一层梁端弯矩等于节点上下柱端弯矩之和。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






