有了荷载向双向传递的概念,对双向板的分析就有了方便的办法。
双向板的内力分析要用弹性理论,是比较复杂的。下面介绍一种称为板带法或板条法的内力分析方法。这种方法是用计算梁的方法来设计板。
板条法的基本原理是选择内力场满足平衡条件。对每一个dx×dy的板单元,其平衡方程为
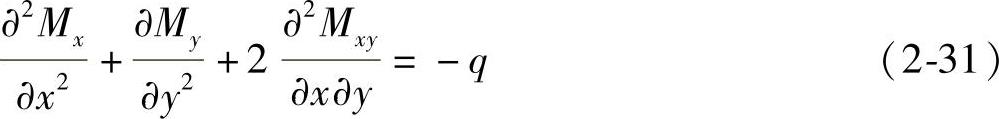
式中 q——为单位面积板上的横向荷载;
Mx——沿x方向单位长度上的弯矩;
My——沿y方向单位长度上的弯矩;
Mxy——单位长度上的扭矩,Mxy=Myx。
由极限理论的下限定理,任何一组在板内各点均能满足平衡条件并满足屈服条件的Mx、My和Mxy都是可行的解。当然所配置的钢筋应能承担这些弯矩。求板的极限荷载的塑性铰线法根据的是下限定理,简单的板带法取Mxy=0,则平衡方程简化为

这一方程可分解为两部分

在式(2-33)中,k为x方向板带承担的荷载比例,(1-k)为y方向板带所承担的比例。当k=0时,全部荷载全由y方向板带承担,取k=1时全部荷载由x方向板带来承担。板带法设计要点之一就是要确定板的荷载分区,选定适当的k值以后,每一个方向的板带内承担的荷载就和梁的荷载一样,完全可用单向梁的分析方法分析内力。
理论上,荷载向两个方向的分配系数k可以任意选择。不同的选择会导致不同的钢筋布置,会有不同的经济效果。设计者的目的就是要使配筋布置经济合理的同时,又保证安全,并应避免在使用荷载下出现过大的裂缝和挠度。下面以一方形板为例说明采用板条法设计的荷载分区分配的方法。
如图2-21所示为一四边简支正方形板,受均布荷载q。取整个板为一区,荷载分配系数取k=0.5,即两个方向均承载q/2。
所有板带的最大设计弯矩为:
Mx=My=ql2/16=0.0625ql2
式中,Mx、My分别为沿x方向和y方向单位长度上的极限弯矩。
若按弹性理论,可由lx/ly=1
查表得
Mx=My=0.0429ql2
可见,按k=0.5的板条法设计和弹性理论相比,高出31%。按这一方案配筋显然是安全的,但是很不经济。
另一种方法是按图2-22所示,将荷载分区分为角区、边区及中间区,每一区内的荷载按最短路线传到支座,在路线距离相同的情况下同时向两邻支座传递。荷载分配系数如图2-22所示。

图2-21 两个方向荷载均匀分配的方板

图2-22 对角线附近的荷载均分给两个方向的方板
这种分区决定了每一方向有两种板带。例如在x方向有边缘板带和跨中板带。对边缘板带,其受荷只有角区内受q/2荷载,最大弯矩为:

对跨中板带,其最大弯矩为:
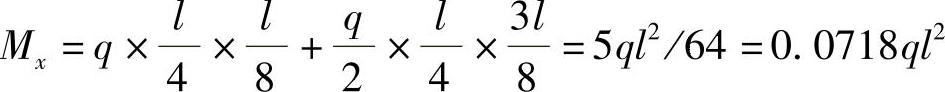
弯矩Mx在y方向的分布呈台阶形,在相同弯矩的板带内配筋相同。按这一方式配筋,中间板带配筋多,靠边上的板带配筋少,显然是合理的,配筋也是方便的。因板带法求出的是下限值,故可保证极限荷载高于实际荷载,是安全的。按这一方法配筋,沿全长方向的平均弯矩值为
Mx=(0.0781×0.5l/l+0.0156×0.5l/l)ql2=0.0468ql2这一值很接近按塑性铰线分析求得的极限弯矩值(0.0418ql2),可见,按这一分配方式也是经济的。这种分析方法比弹性理论简单,比塑性铰线法也方便些。
由以上例子可以看出,由于忽略了扭矩,对每一板条的受力情况完全和梁一样,求梁的内力及弯矩对工程师来讲是很熟悉的,也是简便的。至于荷载分区,工程师可按一般弹性理论的知识作指导。为了控制挠度,可按一般规范控制板厚。由以上分析可知,板带法确实为工程师提供了一种概念清晰、计算简便、保证安全的一种板的设计方法。
板带法对一些特殊支承板更有其方便之处。下面举几个例子。
①四边简支矩形板
对于矩形板,在板的长边中部,其荷载向短跨方向传递,只在短边及角处向长边或角边传递,如图2-23所示。

图2-23 四边简支矩形板
取角边缘带宽为ly/4(短边长的1/4)是合理的。荷载传递方向如图2-23所示。这样各板带的跨中弯矩为:
长边方向(x方向) 边缘板带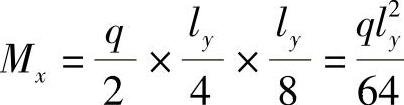
中间板带
短边方向(y方向) 边缘板带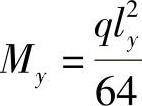
中间板带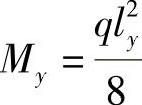 (https://www.daowen.com)
(https://www.daowen.com)
这种分配法,在每一板带内,弯矩为一个值,可直接据此选配钢筋,而且总是偏于安全的。分区适当,可达到简单而经济的目的。
②两边固定、两边简支矩形板
【例2-4】 两边固定支座、两边为简支的矩形板如图2-24所示。受均布荷载q,用板带法求其极限弯矩。

图2-24 【例2-4】两边固定和两边简支的矩形板
【解】 取x方向边长为a,y方向边长为b,b<a,其荷载分区如图2-24a,
靠简支边板带宽为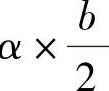 ,显然应取α<0.5,以使靠固端边的板带宽一些。
,显然应取α<0.5,以使靠固端边的板带宽一些。
x方向的受荷如图示,其中间板带弯矩分布为:
跨中正弯矩
固端支座负弯矩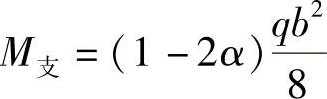
在x方向中间板带负弯矩与正弯矩之比为
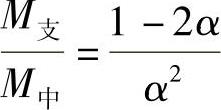
x方向的边缘板带,因近支座处荷载为 ,
,
故跨中弯矩
支座弯矩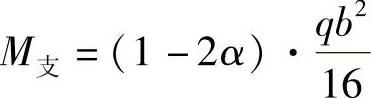
y方向中间板带为均布荷载,按一端固定一端简支的梁分配支座及跨中弯矩
跨中弯矩
支座负弯矩
y方向边缘板带
跨中正弯矩
支座弯矩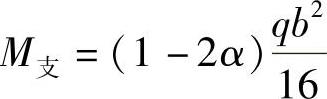
为使M支/M中在1.5~2.5之间,可取α=0.4左右,即可得到满意结果。
【例2-5】 四边固端支承矩形板,尺寸如图2-25所示。承受均布荷载,活载加恒载的设计值为12kN/m2,试用板条法求x、y方向的设计弯矩。
【解】 荷载分区,取边、角板区宽度为短跨的1/4,即6m/4=1.5m。荷载传递方向如图2-25所示。选支座弯矩与跨中弯矩之比为2∶1。弯矩计算如下:
x方向中间板带:
悬臂弯矩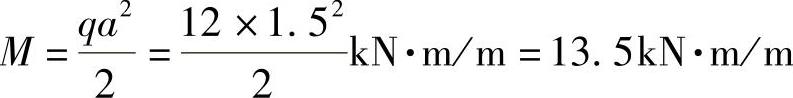
负弯矩
正弯矩
x方向边缘板带:
悬臂弯矩
负弯矩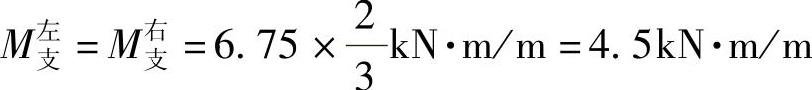

图2-25 【例2-5】
正弯矩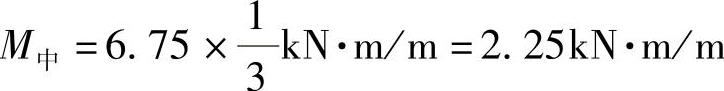
y方向中间板带:
悬臂弯矩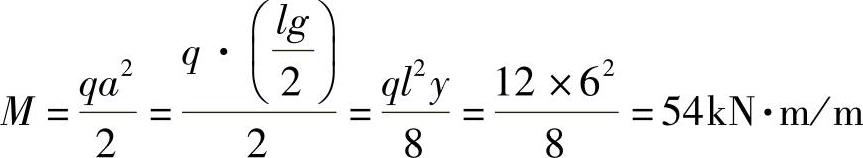
负弯矩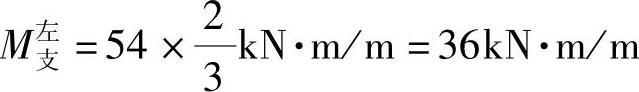
正弯矩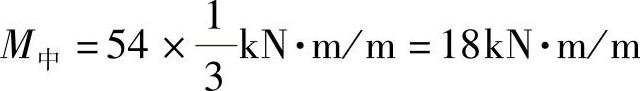
y方向边缘板带:
悬臂弯矩
负弯矩
正弯矩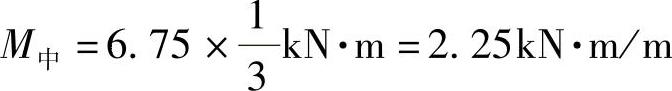
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








