对于技术设计阶段的结构分析，可运用先进的计算机软件，选择正确的、精确的计算简图，建立精细的计算模型，进行正确的分析。对于方案设计阶段，则着重于手算和快速估算。只要定性不差，估算在一定限度内又偏于安全就可以了。

如图2-11取二跨连续梁，AB跨受均布荷载。如果BC跨i₂很大，则AB跨可视为B端固定的梁，跨间最大弯矩为ql²/16，支座弯矩为ql²/8；若i₂很小，则AB跨相当于简支梁，跨中弯矩为ql²/8。如果i₁=i₂，则AB跨的跨中弯矩介于ql²/16与q²/8之间。作为方案阶段估算，取ql²/8是安全可靠的，而仔细计算则接近ql²/10。对于单跨刚架，也有类似情况。若采取梁柱铰接，则横梁相当于简支；若立柱与梁固接，且立柱线刚度很大时，则横梁两端相当于固接，一般则介于两者之间见图2-11。为快速做出决断，最好记住简支梁和悬臂梁在均布荷载及集中荷载作用下的最大弯矩与最大剪力，见图2-12。

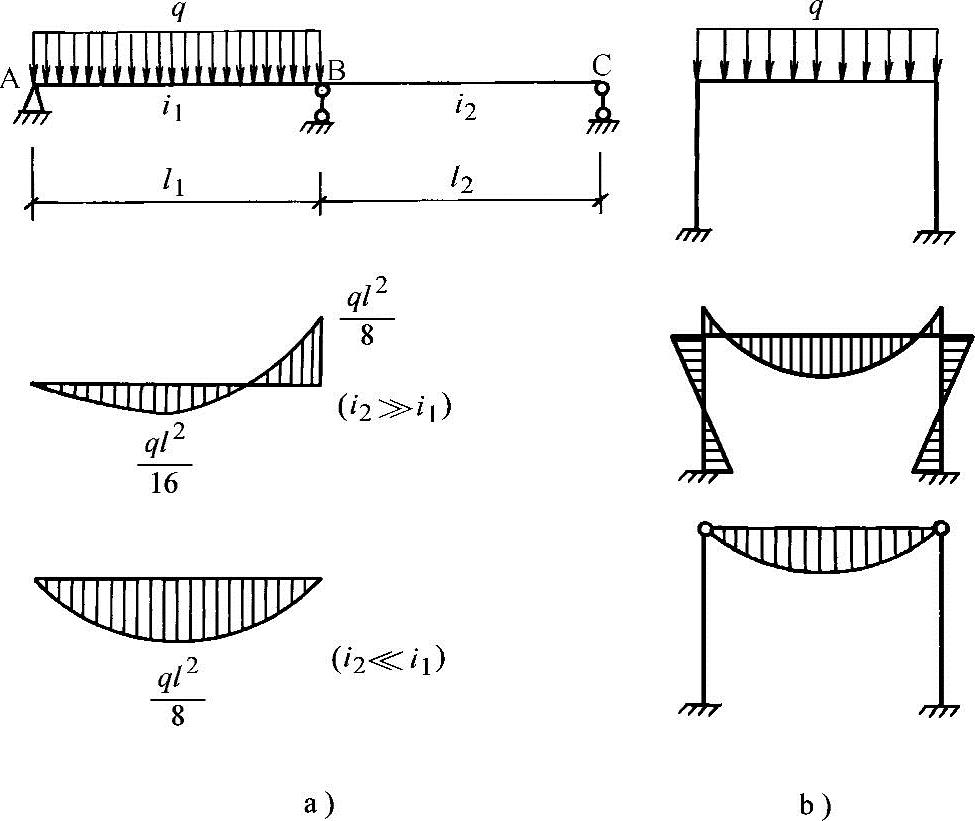
图2-11 连梁、刚架刚度对内力的影响

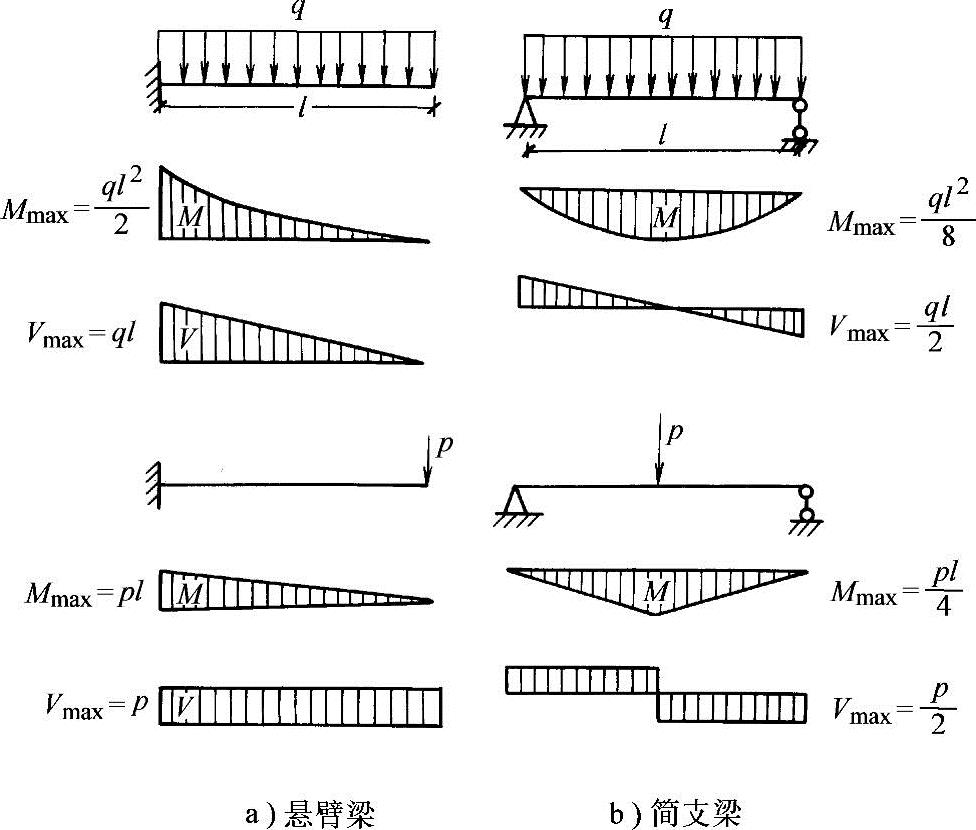
图2-12 单跨梁的弯矩和剪力图

对于梁，ql²/8是一个很重要的数值。任何一根单跨梁（包括从连续梁及刚架梁中取出的单跨梁）受均布荷载后产生的弯矩，如将支座弯矩连一直线，则连线中点与跨中弯矩绝对值之和必为ql²/8。对于固端梁（图2-13），正弯矩与负弯矩在梁中间有一交点，称为反弯点，因该点弯矩为零，也可视作铰点（虚铰点）。对固端梁，反弯点之间的距离为l/3=0.577l≈0.6l，余下的两端之长各

为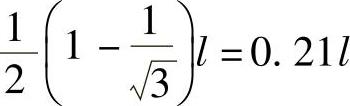。记住，在手头无资料可查时，取离支座0.2l为反弯点，中间按简支梁来计算弯矩，两边按悬臂梁来计算弯矩，则可以供估算之用。例如，对两端固定梁：

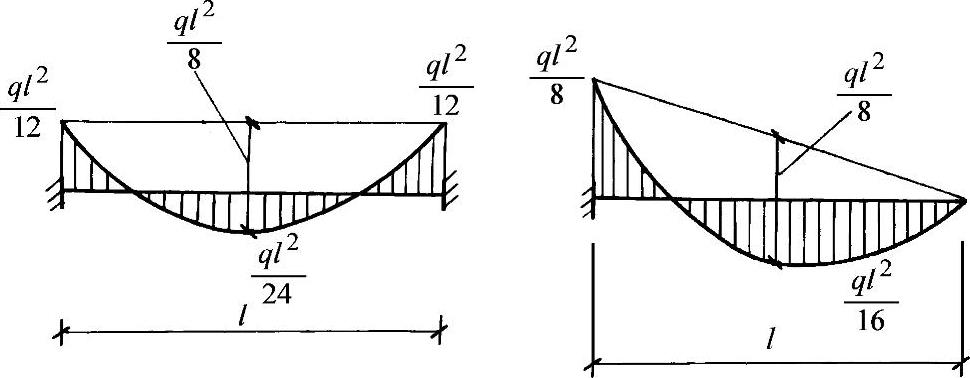
图2-13 单跨梁弯矩图

跨中弯矩为

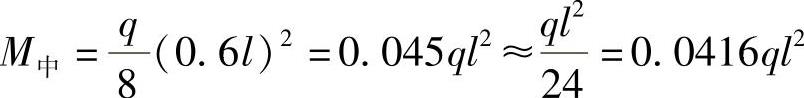
支座弯矩可用两种办法计算，一是两端按悬臂梁计算，0.2l长的悬臂梁受均布荷载q及端点受0.6ql/2的集中力：

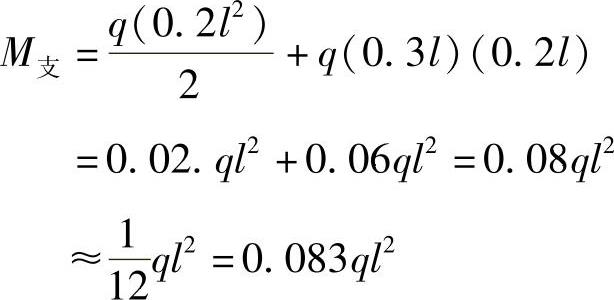
二是用支座弯矩连线之中点与跨中弯矩之绝对值之和为ql²/8，则可得：(www.daowen.com)

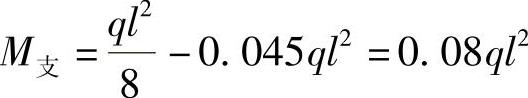
与上述计算结果一致。这种估算与精确解相比已有很好的精度。

有了ql²/8及反弯点的概念，有很多复杂的结构，均可由此做出宏观的估算。

例如：对于上、下弦平行的桁架高度为H，受均布荷载q时，其上、下弦的内力N可按下式推算。

上弦为压力，下弦为拉力。

又如两铰拱结构（图2-14a），可以看作两端有推力的曲梁，其推力可能由拱脚的基础或拱的支承结构承受，若拱的矢高为f，则其水平推力可由下式计算

对于悬索结构（图2-14b），是与拱相反的拉力结构，其对支座的水平拉力为

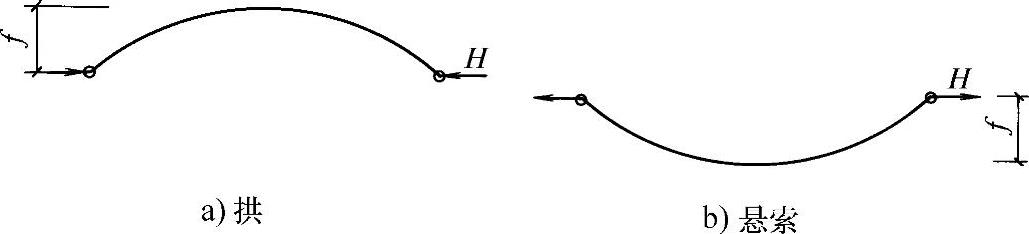
图2-14 拱和悬索的水平反力

有了水平分力，则支座之总反力可由力的合成（或分解）原理求得。