房屋的水平作用力有风荷载、地震力、土压力、水压力、起重机或其他车辆的制动力等。对于一般房屋，方案阶段的整体分析中最重要的水平作用力为风荷载和地震力。
1.风荷载
在非地震区，风荷载是房屋所承受的主要水平力。在方案阶段的总体分析中，一般只需考虑作用在房屋的风荷载合力HW，它是作用在房屋迎风面及背风面上风荷载标准值的合力。要计算风荷载合力，首先要确定风压（单位面积上的风荷载值）。
对建筑物的风压值，是由基本风压乘以修正系数后得到的。基本风压，由各地气象站关于风速的统计资料按50年一遇的可能的最大风速推算得出。统计的风速是在空旷地段、10m高处取10min的平均风速进行的。然后取风压公式ω=v2/1600推定的。《荷载规范》规定可以按建筑所在地的统计风速进行风压计算。在没有统计资料时，可按《荷载规范》给出的全国基本风压分布图求得。例如北京为0.45kN/m2，上海为0.55kN/m2，广州为0.5kN/m2等。对高层建筑，要求按100年一遇的大风设计，这时可将基本风压乘以1.1的系数。
由基本风压可以求得风荷载标准值。
建筑物所处高度不可能恰好为10m，周围地形不一定为空旷平坦，因而必须对基本风压进行修正。此外，前面推导的风速与风压的关系是基于自由气流碰到障碍面而完全停滞所得到的。但一般工程结构物并不能理想地使自由气流停滞，而是让气流以不同方式在结构表面绕过，因此实际结构物所受的风压还不能直接应用，而需对其进行修正，其修正系数与结构物的体型有关。
于是，当计算垂直于建筑物表面上的风荷载标准值时，可按下述公式计算：
ωk=β·μs·μzω0 （2-3）
式中 ωk——风荷载标准值（kN/m2）；
μs——风荷载体型系数；
μz——风压高度变化系数；
ω0——基本风压（kN/m2）；
β——当计算主要承重结构时为高度z处的风振系数βz；当计算围护结构
时为高度z处的阵风系数βgz。
关于高度修正系数。根据实测结果分析，平均风速沿高度变化的规律可用指数函数来描述，即
式中
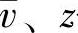——任一点的平均风速和高度；
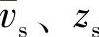——标准高度处的平均风速和高度，大多数国家的基本风压都规定标
准高度为10mm；
α——与地貌或地面粗糙度有关的指数，地面粗糙程度越大，α越大。
为应用方便，我国《建筑结构荷载规范》将地面粗糙度分为A、B、C、D四类，对每一类的风压高度系数列成表格，见表2-8，可直接查用。
表2-8 风压高度变化系数μz
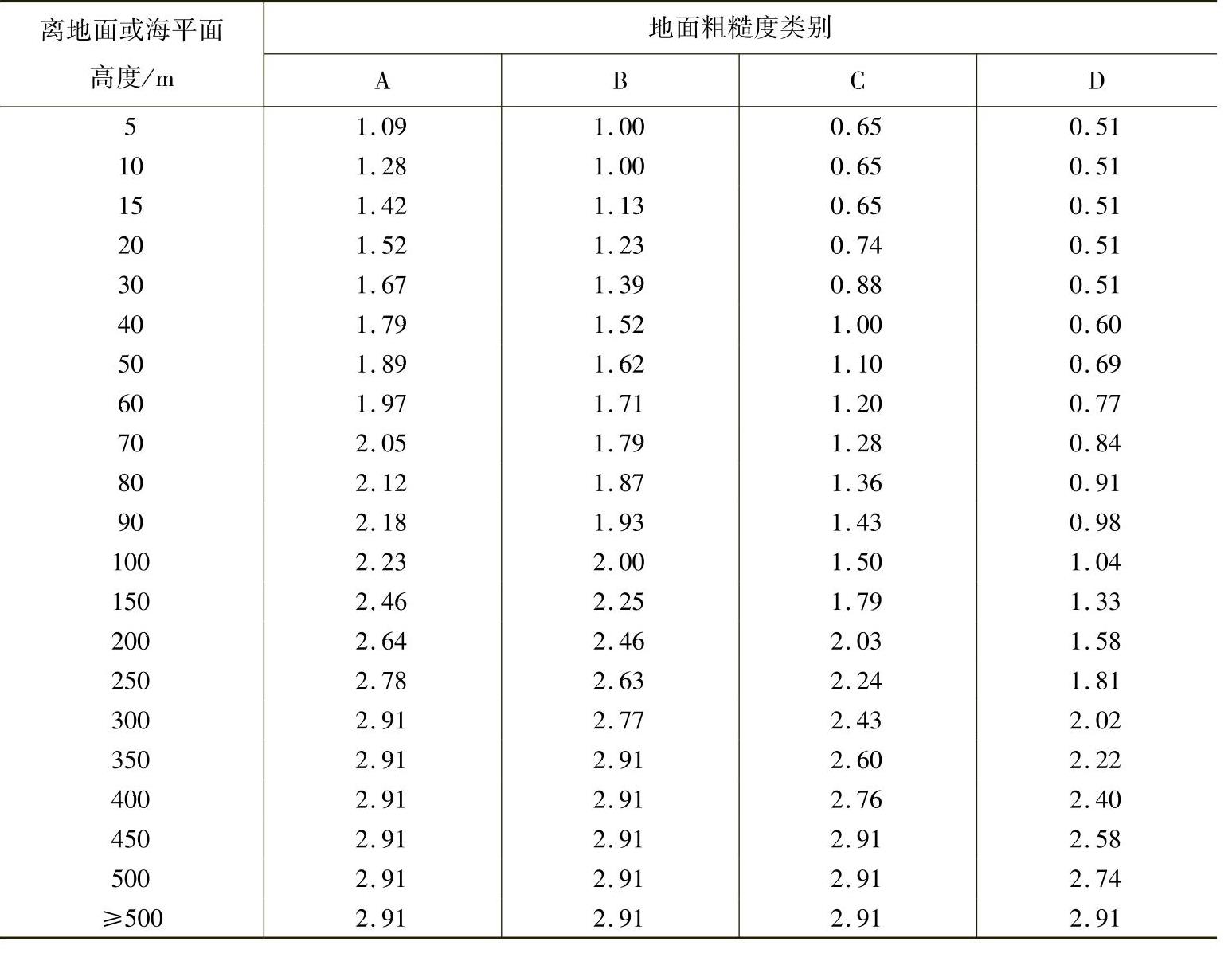
表中：A类指近海海面和海岛、海岸、湖岸及沙漠地带；B类指田野、乡村、丛林、丘陵及房屋比较稀疏的乡镇和城市郊区；C类指有密集建筑群的城市地区；D类指有密集建筑群且房屋较高的城市。
关于体型系数。房屋体型不同将直接影响风的方向和流速，改变风压大小。一般迎风面的风荷为压力，背风面的风荷载为吸力（μs为负值），房屋受到的总的风荷载应为迎风面风荷载和背风面风荷载的叠加，即μs=（μs1-μs2），见图2-2。
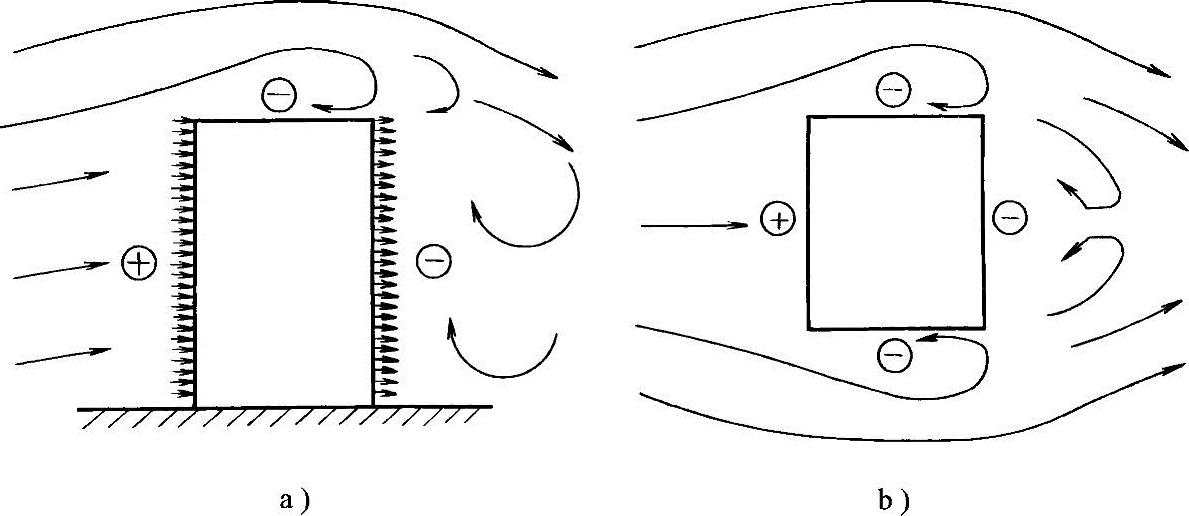
图2-2 风吹形成的正压及负压
目前还没有对各类体型均适合的体型系数计算公式，我国学者对常见的各类建筑物作了系统的试验和分析，并参照国外的先进经验，对常见的房屋和构筑物的体型，给出了风载体型系数，列在《荷载规范》中，可直接查用。对于重要而特殊的建筑物，其体型系数应由风洞试验确定。规范给出的体型系数很多，下面仅给出一般的坡顶房屋和构筑物的体型系数。
风荷载除了引起房屋的倾覆以外，局部吸力也是引起房屋破坏的重要原因，尤其是对坡屋顶的破坏。
根据《建筑结构荷规规范》（GB 50009—2012）有关风载体型系数的规定，当屋面坡度α=30°时，屋面风荷近似为0；当α>30°时，为压力；当α<30°时，为吸力（图2-3）。对于常见的坡屋面，一般α<30°，可见屋面在风荷下通常承受吸力。有一个典型的工程实例，原设计为平屋顶，因屋面防水没有做好，经常发生漏水，后在平屋顶上用木梁改造为α<30°的白铁皮屋面，在一次大风中这
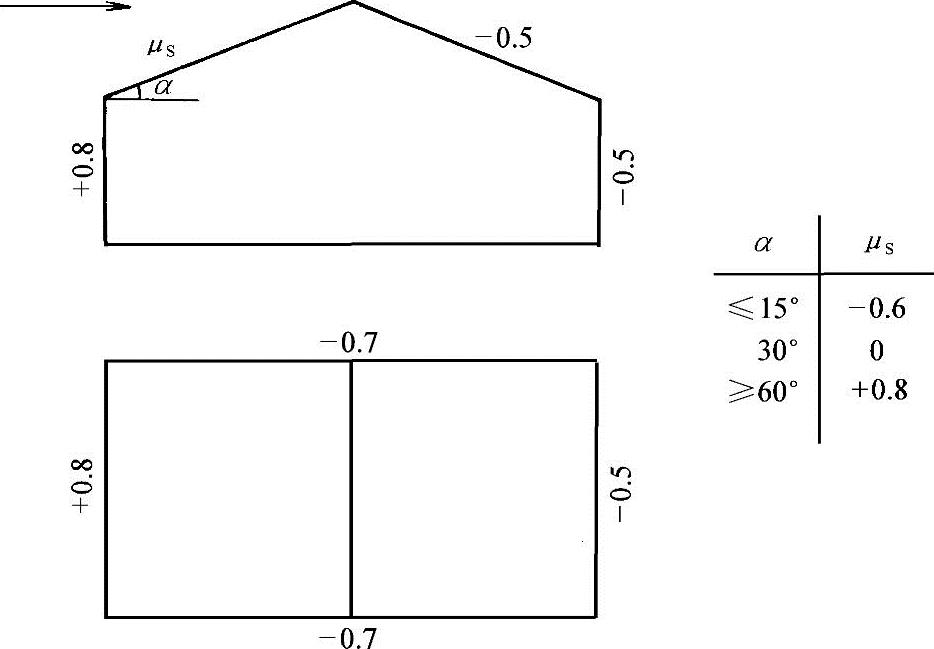
图2-3 坡顶房屋的风载体型系数
个屋面被风荷载完整地吸起，吹翻到了马路上。原因很简单，后改造的木屋盖和铁皮屋面自重很轻，又没有和墙体拉结好，在风荷载吸力作用下被掀起。通常，房屋自重较大，对承受重力荷载有较大的承载力，但设计者往往忽视风荷载吸力的破坏作用，尤其是目前常用薄皮、膜作大跨度结构的屋面，这一点必须引起重视。
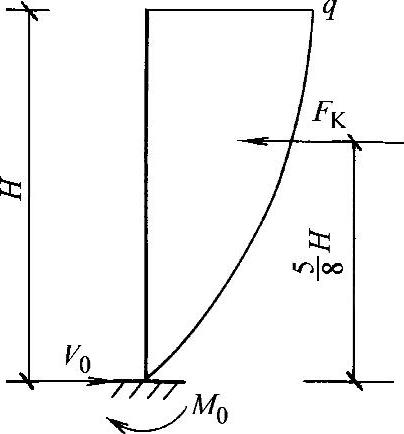
图2-4 风压随高度的变化
结构风压随高度变化的研究表明，由于地表摩擦的结果，使接近地表的风速随着离地面高度的减小而降低。只有离地面300～500m以上的地方，风才不受地表的影响，能够自由流动。而风压与风速的平方成正比，因而风压随高度的变化图，近似为二次抛物线形状，如图2-4所示。因此，可以将结构物所受的风载，近似地按抛物线计算：
风压合力
楼底风剪力 V0=FK （2-6）
楼底风弯矩
【例2-1】 一幢16层办公楼，高50m，平面15m×30m，查得建筑所在地区基本风压值w0=0.45kN/m2，高层建筑，考虑风振系数β=1.70，风压高度变化系数μz按B类地貌取50m高处βz=1.67，试计算楼底的风剪力和风弯矩。
【解】 设风向沿结构公式刚度较弱的短向（图2-5），迎风面体型系数μ1=0.8，背风面体型系数μ2=-0.5，则μs=μ1-μ2=0.8-（-0.5）=1.3。μz=μ50m
=1.67。
建筑物顶点的荷载线集度：
风压合力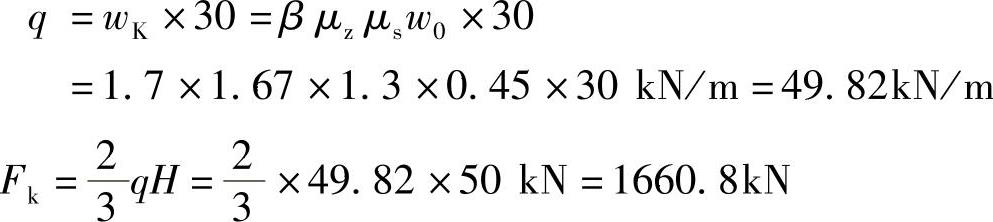
则楼底风剪力可取
V0=Fk=1660.8kN
楼底风弯矩
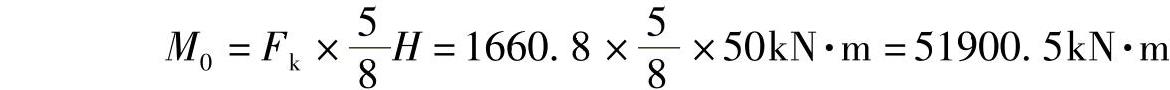
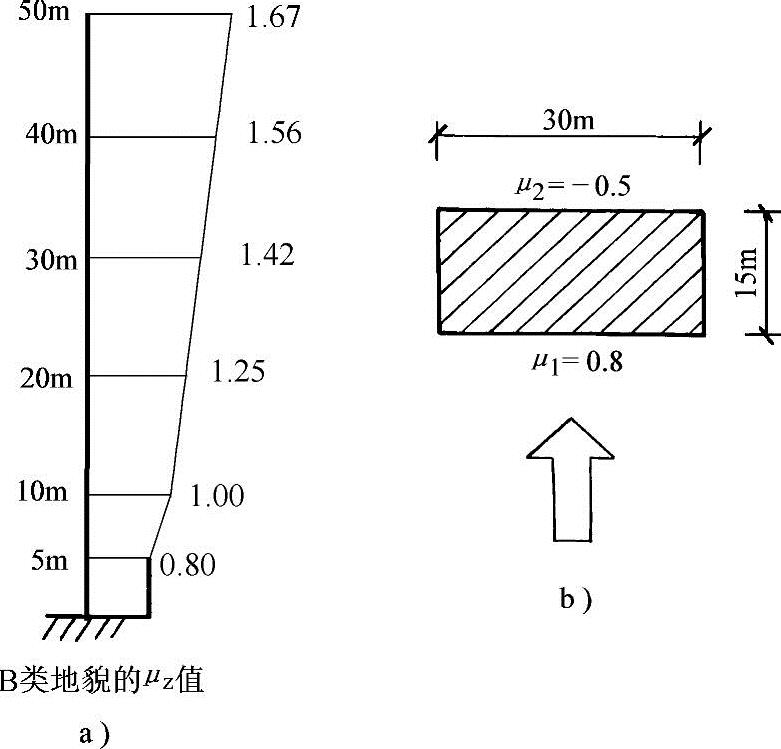
图2-5 【例2-1】
此题如按荷载规范规定的方法计算，结果误差可控制在±10%以内。
如果手边没有手册可查，对于相当一部分城市的基本风压可按ω0=0.5kN/m2估算，风沿高度变化到50m时增大50%，到100m时增加一倍（按B类），风的体型系数可按迎风+0.8，背风-0.5，总的可按μs=1.3计算，这些数据对于初步估算已经可以满足使用了。
2.地震力Heq
地震力是地震时地面运动加速度引起的房屋质量的惯性力。设计中可近似认为建筑物的质量都集中在各层楼面标高处，地震力的大小与地震烈度、建筑物的质量、结构的自振周期以及场地土的情况等许多因素有关。通常地震时既有水平震动又有竖向震动，但一般房屋结构对竖向地震力有较大的承受能力，而水平地震力是引起结构破坏的主要原因，设计中主要考虑水平地震引起的惯性力的影响。通常建筑物顶部质量的惯性力最大，向下逐渐减小，地面及地面以下可以假设为0。在方案阶段的总体分析时，一般只考虑房屋侧向地震力合力Heq的作用效应（图2-6）。
图2-6 地面运动和地震荷载
FE=αG （2-8）
式中 G——房屋总重；
α——与地震烈度、结构自振周期、场地土类别有关的地震影响系数。
（1）水平地震作用估算
对于一高度不超过40m，以剪切变形为主，且质量与刚度沿高度分布比较均匀的多层建筑结构，可采用底部剪力法计算水平地震作用。
底部剪力法是指根据建筑物的总重力荷载，按下式计算出结构底部总剪力（等于总水平地震作用值）的计算方法：
FEK=α1Geq （2-9）然后将此总水平地震作用，按照各层的重力大小Gi及所在高度Hi，分配给各楼层，得到各楼层的水平地震作用Fi：
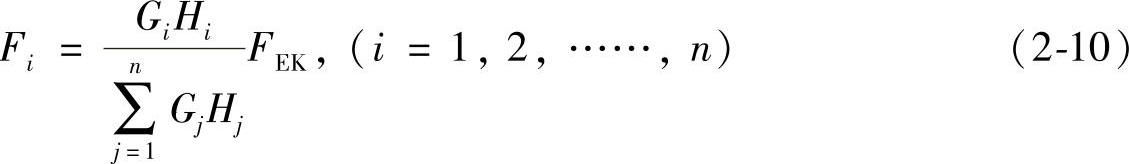
式中 Geq——结构的等效总重力荷载代表值，单质点取GE，多质点取0.85GE，
α1——相应于结构基本自振周期T1的水平地震作用影响系数α；
T1——结构的基本自振周期。
地震影响系数
式中 T——结构自振周期；
Tg——卓越周期，主要与场地有关；
αmax——与地震烈度有关的地震影响系数最大值，取值
见表2-9。
其中，多遇地震αmax用于结构计算，以保证小震不坏，中震可修；罕遇地震αmax用于变形控制验算，以保证大震不倒。
图 2-7
（2）结构自振周期计算
关于结构基本自振周期可用以下几种方式估算：经验公式、半经验半理论公式和有限元计算公式（近似于理论公式），均可作为概念设计估算之用。(www.daowen.com)
1）经验公式。经验公式常针对特定类型的结构，局限性大，但应用方便简捷。
表2-9 水平地震影响系数最大值 （阻尼比0.05）
多高层框架、框架—剪力墙结构，其经验公式为：
或T1=（0.07～0.09）N （2-11b）
式中 H、B——建筑物的总高、总宽；
N——建筑物层数。
高层钢筋混凝土剪力墙结构，高度为25～50m，剪力墙间距为3～6m的民用建筑：
横墙间距较密时：
T1横=0.054N （2-12a）
T1纵=0.04N （2-12b）
横墙间距较疏时：
T1横=0.06N （2-13a）
T1纵=0.05N （2-13b）
或
式中，H、B、N的含义同上。
2）半经验、半理论公式
①多层及高层钢筋混凝土框架、框架—剪力墙结构。这类结构当重量和刚度沿高度分布比较均匀时，按等截面悬臂梁作理论计算，可得按顶点位移确定周期的计算公式：
式中 ΔT——计算基本周期用的结构顶点假想侧移，即把集中在楼面处的重量Gi视为作用在i层楼面的假想水平荷载，按弹性刚度计算得到的结构顶点侧移（m）；
α0——基本周期的缩短系数。考虑非承重砖墙（填充墙）影响，框架取α0=0.6～0.7，框架-剪力墙取α0=0.7～0.8（当非承重填充墙较少时，可取0.8～0.9），剪力墙结构取α0=1.0。
②多层及高层钢筋混凝土框架结构（以剪切变形为主）。采用以能量法为基础得到的基本自振周期计算公式：
式中 Gi——i层结构重力荷载；
Δi——把Gi视为作用在i层楼面的假想水平荷载，按弹性刚度计算得到的结构第i层楼面处的假想侧移；
N——楼层数；
α0——缩短系数，取值与式（2-15）同。
③框架—剪力墙结构。在采用微分方程解无限自由度体系方法的基础上，可以由图2-8查出φj值（j=1、2、3），由式（2-17，计算自振周期，即可计算第1、2、3振型的周期，适用于沿高度方向刚度均匀的结构。
式中 w——结构沿高度方向单位长度的重力荷载值；
g——重力加速度；
EJw——框架—剪力墙结构中所有剪力墙的总等效抗弯刚度；
φj——系数，由图2-8根据刚度特征值λ值查得：
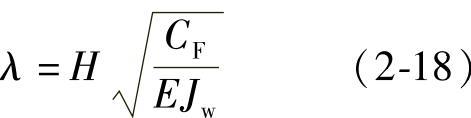
H——结构总高度；
CF——框架的总抗推刚度。
如果粗略估算，也可用下列公式估算多高层建筑物的自振周期：
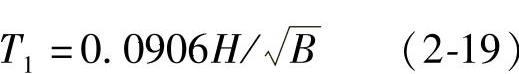
T1的单位为s，H为建筑物总高，B为与地震作用方向平行的总宽（一般为横宽）单位为m。
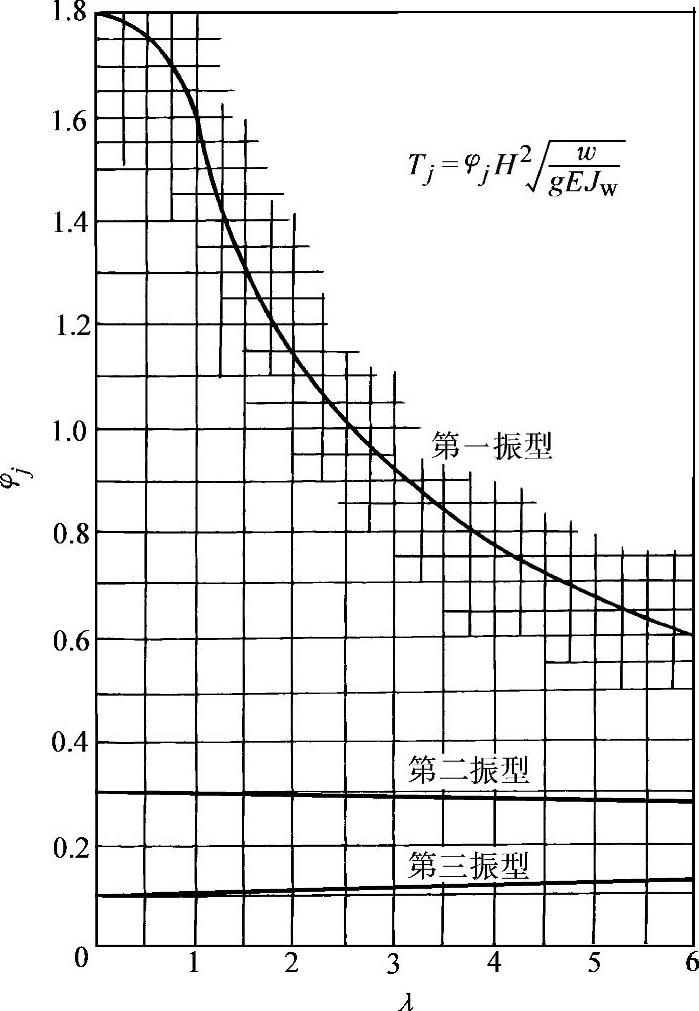
图2-8 框架—剪力墙结构自振周期系数
在实际工程设计中，如果现场地质条件为中软或中硬场地土，抗震设防烈度为7度，这时各类建筑物所受的总水平地震作用（标准值）可估计为：
2～6层砌体结构建筑物T1=0.3～0.5s
FEK=（0.05～0.07）Geq （2-20）
2～8层钢筋混凝土框架结构建筑物
T1=0.6～1.2s
FEK=（0.02～0.08）Geq （2-21）
8层以上高层建筑物T1=1.2～4.0s
FEK=（0.006～0.04）Geq （2-22）
当抗震设防烈度为8度和9度时，FEK值分别为上述各值的2倍和4倍。所有水平地震作用均可能作用于建筑物的横向或纵向，且有往复性。
在一般建筑物设计中，不必考虑竖向地震作用，只有在抗震设防烈度为9度及9度以上的地区，才需要考虑竖向地震作用问题（8度时的大跨度结构也需考虑）。
（3）水平地震作用沿建筑物高度的分布
上述水平地震作用是指地震时在建筑物上产生的总作用。实际上，对多层、高层建筑物来说，不宜将质量集中到一点而需要分成几个相对集中的点，比如，多层建筑物可将全部重力荷载按比例集中到各个楼面和屋面标高处，当然由此也就出现了多质点体系的水平地震作用问题，也即FEK的沿建筑物高度分布问题。对高度不超过40m以剪力引起的弯曲变形为主、且质量和刚度沿高度分布都比较均匀的建筑物，均可假定沿高度各质点的加速度反应与各质点所在高度成正比。为此，可以认为水平地震作用沿建筑物高度为倒三角形分布。
对于一个高度为H，质量沿高度均匀分布的筒体结构建筑物，当总水平地震作用为FEK时：建筑物高度为H的顶部的地震作用为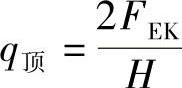
，设地震作用沿高度分布为倒三角形，则高度y处的水平地震作用为（图2-9a）：
对于质量和刚度沿高度均匀分布的多质点建筑物，结构计算简图如图2-9b，质点i的水平地震作用的标准值为
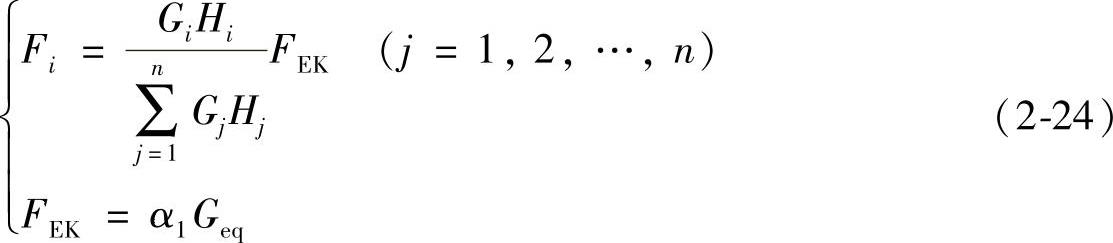
式中，FEK、Geq、α1如前述（对多质点建筑物，Geq取总重力载荷的85%）；Gi、Gj、Hi、Hj分别为集中于质点i、j的重力荷载和i、j点的计算高度。对于T1>1.4Tg的多高层结构，结构顶层应附加集中力σnFEK，作粗略估计σn可取5%。
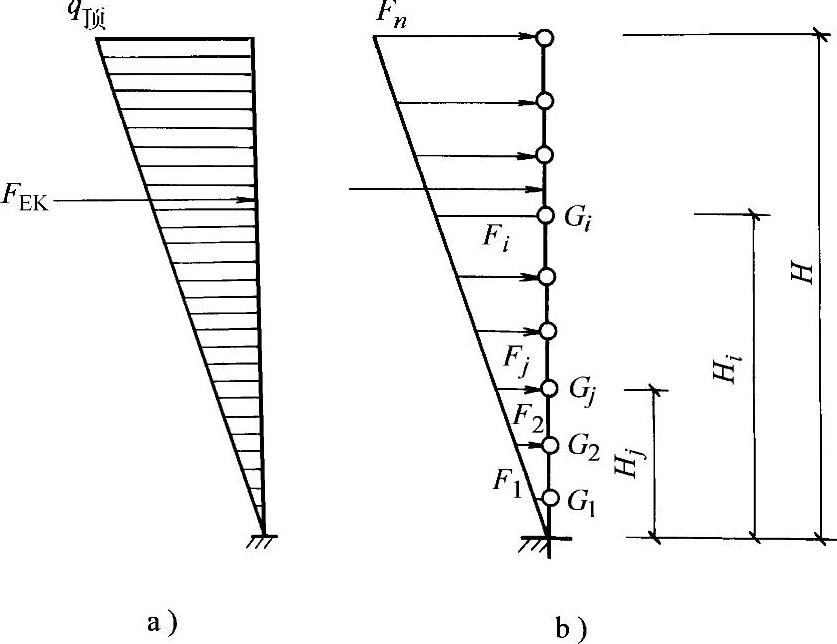
图 2-9
（4）竖向地震作用
在一般建筑设计中，不必考虑竖向地震作用。规范规定抗震烈度9度区的高层建筑（或8度区的大跨度结构），才考虑竖向地震作用。计算方法仍类似于式（1-6）和式（1-8），但α要用竖向地震影响系数的最大值。从估算角度说，设计烈度为8度及9度时，分别取该结构或部件重量的10%和20%作为竖向地震作用力就可以了。
【例2-2】 若一个10层框架结构，总重为46080kN，若地震设防烈度为8度，10层框架按α=0.06估算，建筑物重力荷载和刚度沿高度分布均匀，层高h=4m，求地震作用沿高度的分布和可能使建筑物总体倾倒的倾覆力矩Mov。
【解】 按水平地震作用标准值的取值方法取
FEK=0.06Geq=0.06×46080kN=2764.8kN
各层水平地震作用按式（2-24）求得：
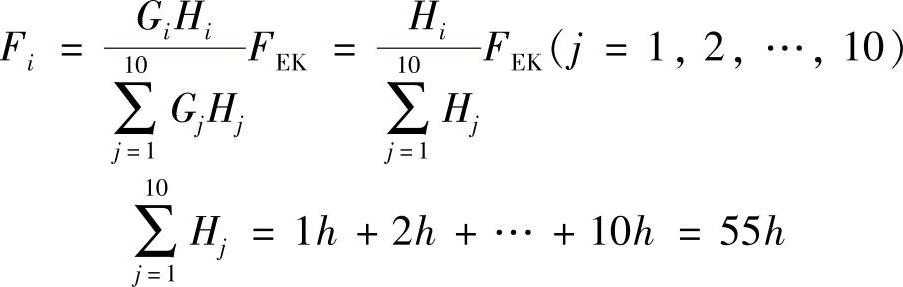
代入上式得（图2-10a）：
F1=50.27kN，F2=100.54kN，F3=150.8kN，…，F10=502.7kN。
倾覆力矩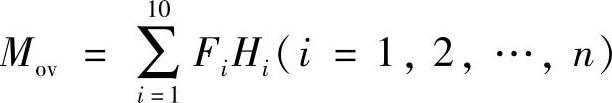
Mov=（50.27×1+100.54×2+…502.71×10）h
=19354.05h=77416.2kN·m
按倒三角形分布规律（图2-10b）有
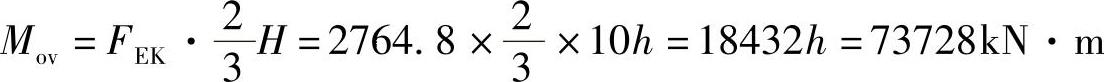
与较精确的计算，其误差约为-4.8%。可见误差不大，可按估算法进行概念设计和选型。
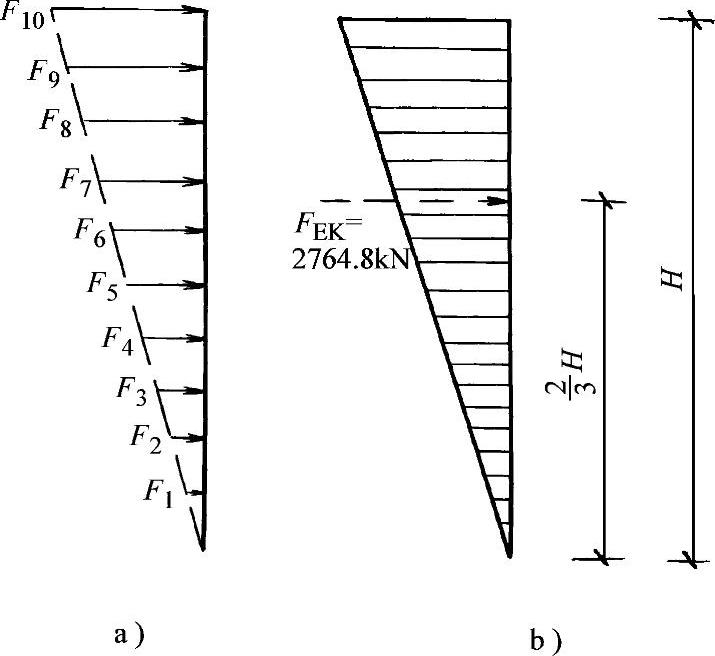
图2-10 【例2-2】水平地震作用沿高度分布
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
