考虑如图6-1所示的多层公路结构，连同路面在内的总层数为n+1层，整个公路结构置于刚性基岩上，第j层结构层用符号Lj表示，则最后一层表示为Ln+1。第j层厚度为hj=zj-zj-1，zj和zj-1分别为Lj层上界面与下界面到路面顶面的距离。为了获得层状弹性土体的传递-反射矩阵，需将所获得的应力、位移响应分量中的指数项e±αpz及e±αsz从一般解中提取出来，同时，利用aje-αpjzj、bjeαpjzj-1、cje-αsjzj、dje-αsjzj-1来分别代替第j层土体的4个积分常数A(ξ)、B(ξ)、C(ξ)和D(ξ)。经过一系列处理后，第j层土体的位移及应力响应分量在波数域中的解答可表示成如下矩阵形式:

为了简化处理，上述推导过程中省略了简谐因子eiωt。上述表达式中，ψj(ξ，z)4×1为波数域内第j层土体的位移及应力响应分量;分别为第j层土体任意深度z(zj-1≤z≤zj)处的下行波矢量和上行波矢量;通过求解各层土体的上、下行波矢量即可获得每层土体的动力响应解。

通过方程(6-10c)和(6-10d)，可获得如下关系:

根据方程(6-10c)、(6-10d)以及方程(6-11a)、(6-11b)，第j层土体任意深度z(zj-1≤z≤zj)处的下行波矢量和上行波矢量可写成如下矩阵形式

其中Ej(Θ)=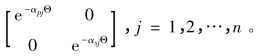

通过上述分析可知，每层弹性土体有4个未知积分常数，则整个公路结构共有4×(n+1)个待求积分常数。对于非轴对称问题，可利用本书相同的方法进行推导，只是其每层的待求积分常数为6个。假设公路各结构层之间紧密连结，无相互滑动。则相邻结构层间的位移ur、uz和应力σrz、σzz是连续的，即在界面z=zj处有:

其中矩阵ψj(ξ，z)4×1的表达式如式(6-10b)所示。

利用式(6-10a)，界面z=zj处的连续条件式(6-13)可写成如下矩阵形式:

由式(6-14)可得:

其中

式(6-15)建立起了界面z=zj处第j层土体的上、下行波矢量与第j+1层土体上、下行波矢量之间的相互关系。根据波在层状弹性土体中的传播规律，子矩阵Ru为P波和S波在z=zj界面处的反射和透射矩阵，且各子矩阵的尺寸都为2×2。

如果公路结构层置于刚性基岩上，则第n+1层的底面的位移为零，根据(6-10a)可得到z=zn处的边界条件为:

从式(6-16)可得:

其中Rdgn(ξ)=-［Dun(ξ)］-1Ddn(ξ)。

将式(6-12a)代入式(6-17)中可得:

再结合式(6-12b)和式(6-18)，可得到如下表达式:

根据式(6-15)，第n-1层界面处的连续条件可写成(www.daowen.com)

将式(6-19)代入式(6-20a)，可得到n-1层界面处第n层土体的下行波矢量与第n-1土体的下行波矢量之间的关系为:

其中Tdg(n-1)(ξ)=［I-Run-1(ξ)En(hn)Rdgn(ξ)En(hn)］-1Tdn-1(ξ)。

同理，将式(6-19)代入式(6-20b)中，可得到如下关系:

为了简化分析，引入下列矩阵表达式:

从式(6-21)和式(6-22)可以看出，在n-1层界面处，第n层的下行波矢量Wdn(ξ，zn-1)和第n-1层的上行波矢量Wun-1(ξ，zn-1)都能够用第n-1层的下行波矢量Wdn-1(ξ，zn-1)表示。以此类推，可得到如下关系式:

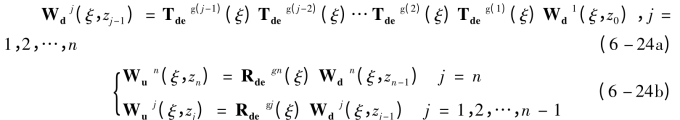
其中Tdegj(ξ)=［I-Ruej(ξ)Rdeg(j+1)(ξ)］-1Tdej(ξ)，j=1，2，…，n-1;

Rdegj(ξ)=Rdej(ξ)+Tuej(ξ)Rdeg(j+1)(ξ)Tdegj(ξ)，j=1，2，…，n-1;

Rdegn(ξ)=-［Dun(ξ)］-1Ddn(ξ)En(hn)，j=n。

从式(6-24a)和式(6-24b)可以看出，任意层的顶面处的上行波矢量Wuj(ξ，zj)可由该层底面处的下行波矢量Wdj(ξ，zj-1)表示，j=1，2，.....，n。而此下行波矢量Wdj(ξ，zj-1)又可由第一层顶面的下行波矢量Wd1(ξ，z0)表示。也就是说每个结构层左边的未知积分常数Wuj(ξ，zj)都可由右边的未知积分常数Wdj(ξ，zj-1)表示，而每层右边的未知积分常数Wdj(ξ，zj-1)又可由顶层右边的未知积分常数Wd1(ξ，z0)表示，各层待求积分常数如图6-1所示。可见，如果获得Wd1(ξ，z0)，则整个层状结构的未知积分常数即可获得。

考虑如图6-1所示的圆形均布荷载作用在路面，轮胎与路面的接触半径为R，荷载的振动频率为ω，则荷载的表达式可写成

其中P为轮胎接地压力，对式(6-25)实施零阶Hankel变换可得:

根据式(6-10)，在波数域内的，路面表面的边界条件可写成:

其中同时利用方程(6-12b)和(6-24b)，可得到如下关系:

将式(6-28)代入式(6-27)中，可获得第一层顶面的下行波矢量Wd1(ξ，z0)为

至此，整个公路结构层的未知积分常数都可由式(6-24a)、式(6-24b)和式(6-29)获得。在得到各层的积分常数后，利用式(6-10a)即可得到弹性层状结构的应力、位移响应在变换域中的传递-反射矩阵解。从上述的推导结果可以看出，所有子矩阵中的元素都只有负指数项，且单个子矩阵的尺寸最大不超过2×2。同时拥有的这两个特点可以避免其他方法所遇到的数值积分困难，使得计算结果更精确。