图6-1　层状公路结构计算模型和汽车荷载作用模式

作用在公路路面上的汽车荷载是以面源的形式分布的，按照公路路面设计规范的要求［172］，路面力学计算时以单轴双轮胎作为基本荷载条件，同时轮胎与路面的接触被假设为圆形分布。此时，可利用极坐标系进行分析。本书公路结构计算模型和汽车荷载作用模式如图6-1所示，公路各结构层动力响应分析时，可先考虑单轮荷载作用，然后再利用叠加原理得到双轮荷载作用下的结果。因此建立如图6-1的坐标系统，单轮荷载作用时问题可简化为轴对称课题。假设公路各结构层材料为均质、线弹性、各向同性介质，根据弹性动力学原理，轴对称情况下弹性介质的位移和应力可由两个势函数φ(r，z，t)、ψ(r，z，t)表示为［173］:

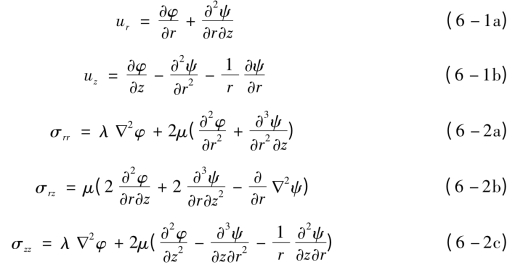
其中，ur和uz分别为径向和轴向应力，λ和μ是弹性材料的Lame常数，∇2=∂2/∂r2+r-1∂/∂r+∂2/∂z2，为Laplace算子。φ(r，z，t)和ψ(r，z，t)分别为压缩波势函数和剪切波势函数，该两个势函数满足如下Helmholtz方程:

式中，cp=，分别为弹性介质的压缩波和剪切波，ρ为材料密度。

本书考虑稳态响应问题，在简谐荷载作用下，公路结构的应力、位移响应分量及两个势函数都满足如下方程

其中Ω(r，z，t)=(ur，uz，σrr，σrz，σzz，φ，ψ)(r，z，t)，代表各响应分量及势函数，e为指数函数，ω为荷载的振动频率。

引入m阶Hankel变换，其正变换和逆变换分别为如下形式:

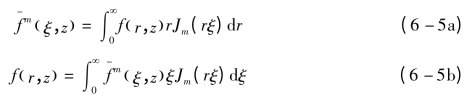(www.daowen.com)

其中Jm(z)为m阶第一类Bessel函数，ξ为轴对称问题径向波数，f和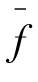分别表示空间域和波数域中的变量。

将式(6-4)代入式(6-3)中，并施加r方向的零阶Hankel变换，则式(6-3)的波动方程可转变为如下偏微分方程组:

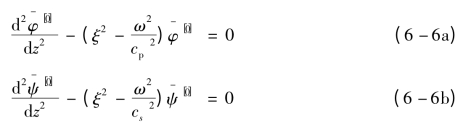
其中，势函数右上角的符号表示Hankel变换的阶数，求解式(6-6)可得到:

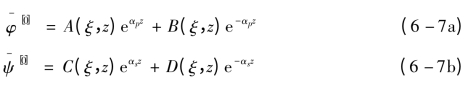
其中，αp=分别为P波和S波的复数波，且有kp=ω/cp，ks=ω/cs。A(ξ，z)、B(ξ，z)、C(ξ，z)和D(ξ，z)为积分常数，由边界条件确定。

对本构方程式(6-1)和式(6-2)施加零阶及一阶Hankel变换，可得到变换域内应力及位移的响应表达式:

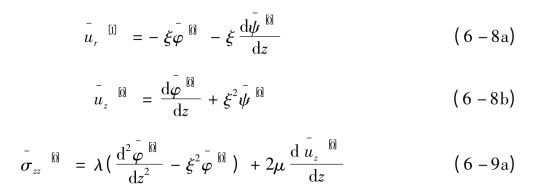
其中∑rr=σrr+2μur/r。

将式(6-7)代入式(6-8)和式(6-9)，即可获得所有的应力分量和位移分量。