模量E、H、Ew和Hw均是净应力和吸力的函数，受净应力和吸力的影响。根据以上的推导，得到用净应力和吸力表示的弹性模量E和H及体积模量Ew和Hw。由于在一定净应力下，吸力和含水量存在一一对应的关系，即式(4-32)，从而得到用净应力和含水量表示的E和H及Ew和Hw。E和H及Ew和Hw中的参数可以通过试验数据拟合得到。下面引用文献［156］的试验数据(见表4-1)，分析含水量和净应力对非饱和土模量的影响。

图4-4为根据式(4-31)得到的常净应力下弹性模量E随吸力的变化曲线。从图中可以看出，在不同净应力下，饱和状态的弹性模量E最小，随着吸力的增大，弹性模量E逐渐增大且逐渐达到稳定值。在低净应力下，吸力对弹性模量E的影响很小;随着吸力的增大，吸力对弹性模量E的影响越来越大。在净应力为0kPa时，弹性模量E随吸力的变化很小，最小值为692.7kPa，最大值为1135.1kPa;当净应力为100kPa时，吸力对弹性模量E的影响很大，最小值为4417.9kPa，最大值为12671.5kPa。图中，净应力对弹性模量E的影响较大，这主要是因为试验用土的初始孔隙比为0.792，压实度为0.866，土体较松散，因此施加净应力能使得土体密实，显著提高其强度。

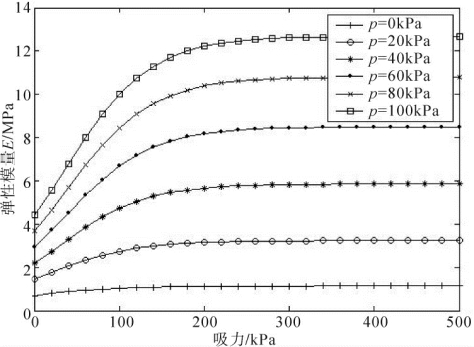
图4-4　常净应力下弹性模量E随吸力的变化曲线

图4-5为常净应力下弹性模量E随质量含水量的变化曲线。从图中可以看出，在一定净应力下，弹性模量E均随着质量含水量的增大单调减小。质量含水量越大，弹性模量E越小，最大弹性模量Emax处于最干状态下，最小弹性模量Emin处于饱和状态下。这说明，降低质量含水量，能有效地提高路基强度。当质量含水量小于0.15时，弹性模量E随质量含水量的变化很小，这一含水量接近于最优含水量0.163，这也验证了在工程中要求将路基质量含水量控制在最优含水量左右的措施的合理性。另外，从图中还可以看出，在低净应力下，质量含水量对弹性模量的影响很小，随着净应力的增大，质量含水量对弹性模量E的影响越来越大。这主要是因为试验用土初始孔隙比较大，压实度低，在这种情况下，增加净应力能进一步压实土体，起到提高土体强度的作用。

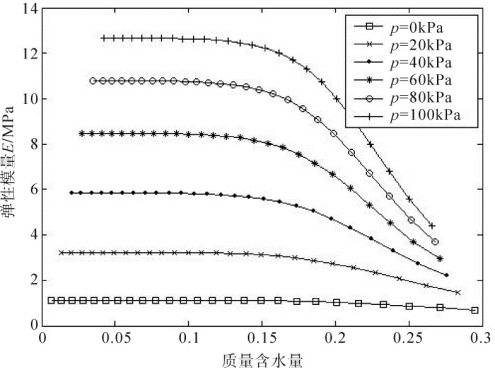
图4-5　常净应力下弹性模量E随含水量的变化曲线

(www.daowen.com)

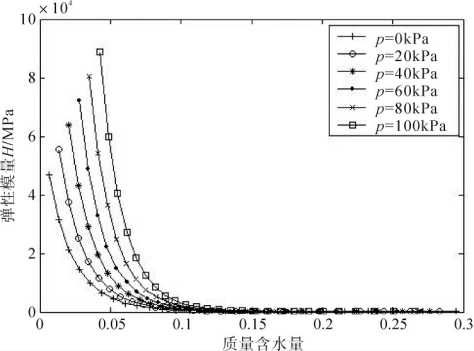
图4-6　常净应力下弹性模量H随质量含水量的变化曲线

图4-6为常净应力下土结构体积变化相对于吸力的弹性模量H随质量含水量变化的曲线。从图中可以看出，质量含水量对弹性模量H的影响很大，随着质量含水量的增大，模量H单调减小。在低质量含水量时，弹性模量H相当大，这是因为低质量含水量段对应于高吸力段，此时吸力的变化基本上不引起孔隙比的变化。另外，净应力对弹性模量H也有影响，在同一质量含水量下，净应力越大，弹性模量H越大。

图4-7为常净应力下3/Ew随质量含水量的变化曲线。由式(4-36)可知，3/Ew=dθ/dp，因此图4-7表示的是dθ/dp随质量含水量的变化曲线。dθ/dp表征的是净应力变化对体积含水量的影响。从图上可以看出，在各种净应力下，dθ/dp均随着质量含水量的增大而减小。在质量含水量较小时，3/Ew＞0，说明此时增加净应力，体积含水量增大;随着质量含水量增大，dθ/dp逐渐减小至小于0，此时质量含水量较高，增加净应力会引起体积含水量的减小。另外，净应力对dθ/dp也有影响。同一质量含水量下，净应力越大，dθ/dp越大。这说明在低质量含水量范围内，净应力越大，增加净应力引起的体积含水量增加量越大;在高质量含水量范围内，净应力越大，增加净应力引起的体积含水量减小量越小。

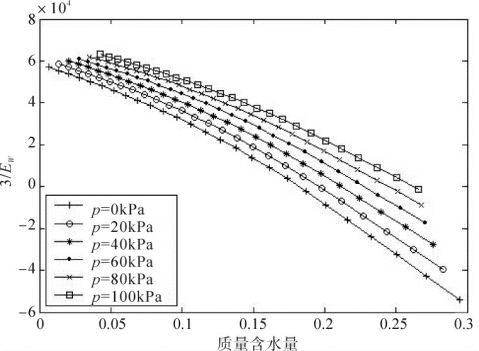
图4-7　常净应力下3/Ew随质量含水量的变化曲线

图4-8为常净应力下1/Hw随质量含水量的变化曲线。由式(4-38)可知，1/Hw=dθ/ds，因此图4-8表示的dθ/ds随质量含水量的变化曲线。dθ/ds表征的是吸力变化对体积含水量的影响。从图上可以看出，在不同的净应力下，dθ/ds均随着质量含水量的增大而减小，且有dθ/ds＜0。这说明增加吸力会使体积含水量减小，且减小的速率随着质量含水量的增大而增大。比较不同净应力下的曲线，可知净应力对dθ/ds有影响。在相同的质量含水量下，净应力越大，dθ/ds值越大，说明净应力越大，吸力变化对含水量的影响越小。这是因为净应力越大，土体越密实，孔隙比越小，土中的平均孔隙尺寸越小，因此土体的持水性能越强，施加相同吸力引起的含水量减小量越小。