式(4-23)和式(4-28)分别描述了非饱和土中固相和水相在净应力和吸力作用下的体积变化。其中，E为净应力(σm-ua)变化引起的土体结构体积变化的弹性模量;H为基质吸力(ua-uw)变化引起的土体结构体积变化的弹性模量;Ew为(σmua)变化引起的水体积变化的体积模量;Hw为(ua-uw)变化引起的水体积变化的体积模量。这4个模量E、H、Ew和Hw均为非饱和土水力和力学计算中的重要参数，可以通过上一节建立的孔隙比和含水量与净应力和吸力的关系求得。

由土结构体积总应变的本构关系，即式(4-3)得到:

又有dεv=，代入式(4-29)后有:

根据孔隙比与净应力和吸力的表达式，可以得到∂e/∂p，代入式(4-30)得到:

其中:

从式(4-31)可以看出，土体的弹性模量受净应力和吸力的影响。净应力和吸力对弹性模量E的影响体现在参数A和孔隙比e上。

又由式(4-28)可知，在一定净应力下，吸力和含水量是一一对应的，即

将式(4-32)代入式(4-31)，可以得到用净应力和含水量表示的弹性模量E。

对于路基中处于一定深度的土，其受到的净应力取决于其上覆土层的重力与行车荷载的大小，行车荷载是一个定值，上覆土层的重力与含水量有关;而吸力取决于净应力和含水量的大小。因此，在理论上，处于一定深度的土，它的弹性模量E仅受含水量的影响。

同理可以得到弹性模量H:(www.daowen.com)

其中:B=

将式(4-31)、式(4-33)代入式(4-9)，可以得到用净应力和吸力表示的非饱和土有效应力参数χ:

由水相体积变化的本构关系，即式(4-10)可以得到

又有θ=Vw/V0，代入式(4-35)得到

将式(4-28)代入式(4-36)得到

其中:C=a1-b1lg(s+c0+c1p)-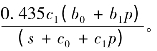

同理得到

其中:D=-