由于采用压力板仪和GCTS压力仪等仪器测土-水特征曲线施加的气压力上限为1500kPa，对于在密实且较低含水量情况下的基质吸力远远大于1500kPa的小洪山黏土，不能满足试验要求，故采用滤纸法测定试验用土在密实状态下的土-水特征曲线。

(1)试验原理介绍

滤纸法是建立在滤纸能够同具有一定吸力的土达到平衡(在水分流动意义上)的假设的基础之上的。土与滤纸之间的水分或水蒸气交换可以达到平衡。当干的滤纸放在土样上，滤纸与土样直接接触，水分便从土中流入滤纸，直至达到平衡。因此，只要测定滤纸平衡时的含水率，根据滤纸的率定曲线(即滤纸含水率与基质吸力的函数关系)，就可以得到滤纸的基质吸力，也即是土样的基质吸力。

本次试验采用杭州新华造纸厂生产的“双圈”牌NO.203型滤纸，该滤纸主要技术指标为:直径，70mm;灰分，0.000035g/张，占质量百分比为0.01%;滤速为慢速。试验过程中保证室内温度为25±1℃，因而不考虑温度的影响;湿度为70%～75%。在这种环境下，滤纸率定曲线如图3-6，率定曲线方程为［155］:

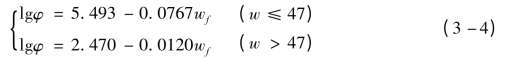
式中:φ(kPa)和wf(%)分别为滤纸的吸力和含水率。

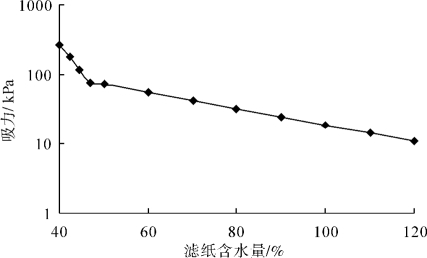
图3-6　“双圈”牌NO.203型滤纸率定曲线

(2)试验设备

试验设备主要有:“双圈”牌NO.203型滤纸，烘箱，恒温箱，精度为0.0001g的电子天平，三轴制样模具，保鲜膜，温度计，湿度计，镊子，干燥器。

(3)试验方案

通过测出6种不同含水量的土样在3种不同干密度下的基质吸力来分析干密度对土-水特征曲线的影响。3种干密度分别为1.70g/cm3、1.75g/cm3和1.80g/cm3(对应压实度分别为90%、93%和96%)，含水量分别为0.14、0.16、0.18、0.20、0.22和0.24，将3种干密度和6种含水量进行组合，每种组合进行3组平行试验。

(4)试验步骤

具体试验步骤如下(见图3-7):

1)根据设计的含水量称取一定量的土样和水，水土拌匀后，放入塑料袋中闷置24h，使配制土含水量均匀。

2)采用三轴制样模具，按照设计的干密度，将配制好含水量的土制成三轴试样。试样大小为直径50mm，高100mm。

3)由于滤纸(直径70mm)断面大于试样的断面(直径39.1mm)，将滤纸裁剪成略小于试样断面大小。为保证中间的一张计量滤纸不直接接触土样，中间的滤纸略小于上下两张滤纸。将裁剪好的滤纸放入烘箱中烘烤若干小时，使滤纸充分干燥。烘干的滤纸冷却后放入干燥器中储存备用。

4)将制好的三轴试样从中间50mm高度处切开，再将切开后的两个断面用小刀刮平，使土样再次合上时能够接触良好。

5)从干燥器中拿出3张滤纸，其中一张滤纸用电子天平称量质量，作为干滤纸质量m0。将3张干滤纸(称量质量的那张滤纸置于中间)重叠放入切开的试样中，再将土样合上，使滤纸和土样充分接触，然后用保鲜膜将土样包裹。

6)将包裹好的试样放入恒温箱中，恒温箱中的温度为25℃，湿度为70%～75%。

7)在恒温箱中存放14d，取出试样，拆开保鲜膜，快速取出中间那张滤纸并称量质量，记为m1。

图3-7　滤纸法试验过程

(5)注意事项

由于滤纸法技术要求很高，操作可能引起的误差较大，试验时必须注意以下事项:

1)土样切开后的两个断面要刮平，保证放入滤纸后，滤纸和土样能接触良好。

2)两次称量滤纸质量时，操作必须十分迅速。滤纸必须在很短时间(3～5s)内称量，以免滤纸与周围大气接触而发生水分变化，对滤纸质量产生影响。

3)用保鲜膜包裹土样时，要将两段土样的断面对接处闭合好;另外，保鲜膜要将土样包裹严实，使两段土样不能有错动。

(6)试验结果

1)数据整理以及曲线拟合。

试样内滤纸平衡后的含水率wf计算公式为:

再根据率定曲线公式(3-4)，得到在某种干密度和含水量下土样的基质吸力。

在制样时，每个试样的含水量都是用质量含水量表示的。在拟合土-水特征曲线表达式时，经常要用到体积含水量或饱和度。在不同干密度下，体积含水量和饱和度与质量含水量之间的换算关系是:

式中:θ——压实样的体积含水量(%);

w——土样的质量含水量(%);

S——压实样的饱和度(%);

n——压实样的孔隙率(%);

Gs——土粒的比重，即土粒和水在标准大气压、温度为3.98℃时密度的比值;

ρd——压实样的干密度(g/cm3);

ρw——在标准大气压、温度为3.98℃时水的密度(g/cm3)。

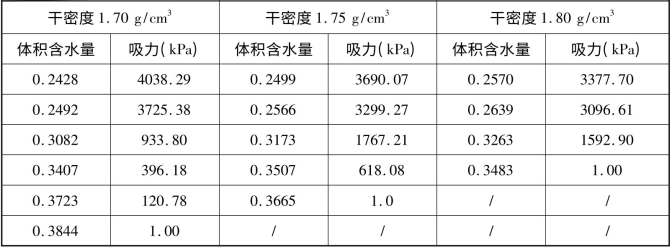
根据以上试验，得到3种干密度下不同含水量对应的吸力值，如表3-5。

下面根据以上试验数据拟合3种干密度下的土-水特征曲线。由于土-水特征曲线是表征非饱和土持水特性和水分迁移特性的重要参数，近年来，不少学者对其进行了深入的研究，越来越多的数学模型被用来描述非饱和土的土-水特征曲线。目前广泛采用的有Van Genuchten模型［151］、Fredlund-Xing模型［150］、分形模型［152］以及包承纲模型［153］等。大量研究表明，Van Genuchten模型对绝大多数土体在相当宽的水势或含水量范围内具有普遍适用性，是最为普遍采用的描述土体持水特征的通用模型，因此，采用VG模型［130］，即式(3-8)，分别对1.70g/cm3、1.75g/cm3和1.80g/cm33种干密度下的体积含水量和吸力之间的关系进行拟合。

表3-5　3种干密度下不同含水量土样的吸力值(www.daowen.com)

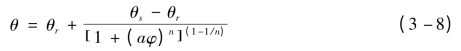
式中:θr——残余体积含水量;

θs——饱和体积含水量;

a，n——拟合参数。

3种干密度下的SWCC拟合曲线表达式为:

拟合曲线如图3-8所示。从图中可以看出，1.70g/cm3、1.75g/cm3和1.80g/cm33种干密度下的数据点与拟合曲线吻合得很好。

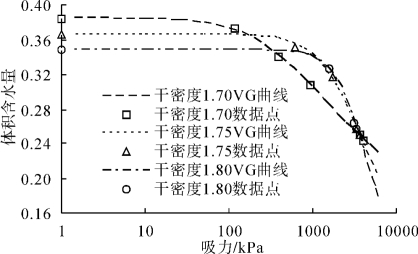
图3-8　3种干密度下的SWCC拟合曲线

2)结果分析。

图3-8为1.70g/cm3、1.75g/cm3和1.80g/cm33种干密度下的SWCC拟合曲线。从图上可以看出，干密度对土-水特征曲线有很大影响。干密度越大，饱和含水量越小，进气值越大，超过进气值后的脱湿速率(即曲线斜率)越大，土体的持水性能越强。这主要是因为土体干密度越大，单位体积内的土粒越多，孔隙越少，孔隙率也就越小，从而导致饱和体积含水量减小;土样干密度越大，孔隙率越小，而土中最可能的孔隙率减小方式是减小土中的大孔隙，土中最大孔隙越小，从而导致气体开始进入土体时对应的吸力值，即进气值越大;另外，当孔隙率减小，土中的平均孔隙尺寸也会减小，导致土体的持水性能增强，脱湿速率减慢。

表3-6　3种干密度的SWCC曲线拟合参数

表3-6为3种干密度下的SWCC曲线VG模型参数的拟合结果。从表3-6可以看出，干密度对土-水特征曲线VG模型的参数有很大影响。下面逐一分析干密度对VG模型4个拟合参数的影响。

饱和体积含水量与干密度之间存在以下关系:

式中符号意义与式(3-7)相同。

由式(3-9)可知，饱和体积含水量随干密度增大而线性减小，图3-9验证了饱和体积含水量与干密度之间的关系。

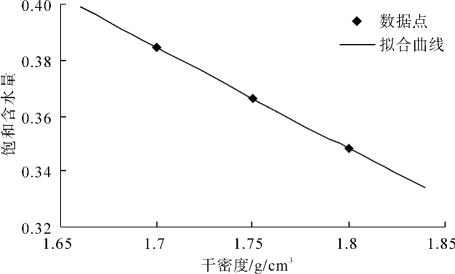
图3-9　饱和体积含水量随干密度的变化

残余含水量指的是土体中含水量随着吸力的增加降低到一临界值后，含水量的继续减少需要增加很大的吸力，这一临界含水量称为残余含水量。这说明土体在含水量大于残余含水量时的脱水速率比达到残余含水量以后的脱水速率大得多，土体对残余阶段土中水的吸附作用比对快速脱水阶段排出水的吸附作用大得多。因此，可以认为在快速脱水阶段在吸力作用下排出的那部分水是土中的自由水，而在残余段排出的水是土中的结合水，即紧密吸附于土颗粒表面的那部分水。那么，单位体积内结合水的体积只与单位体积中的土粒的表面积成正比。当认为土体为均匀介质时，土粒的表面积与土粒的质量成正比，从而得到

式中:mw-res——单位体积中残余水的质量;

ms——单位体积中土粒的质量;

wres——残余质量含水量。

再根据质量含水量和体积含水量的关系，得到

式中:θres——残余体积含水量。

由式(3-11)可知，残余体积含水量与干密度呈线性相关。用式(3-11)对以上试验得到3种干密度下的残余体积含水量进行拟合，得到

结果如图3-10所示。从图中可以看出，试验数据与拟合曲线吻合较好，这也验证了以上对残余含水量的分析以及残余体积含水量与干密度之间的关系。

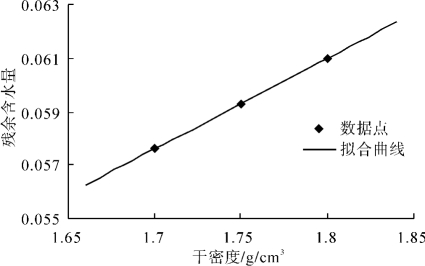
图3-10　残余体积含水量随干密度的变化

在VG模型中，参数a是与土的进气值ψa相关的参数。进气值指的是土水特征曲线边界效应段渐近线与转化段渐近线交点对应的吸力值［131］。从3种不同干密度对应的a值来看，干密度为1.70g/cm3对应的a值远远大于干密度为1.75g/cm3和1.80g/cm3对应的a值。根据作图法，得到3条SWCC的进气值分别为168.13kPa，1134.66kPa和1787.07kPa。从这些数据可以看出，干密度越大，土体的进气值越大。通过数据分析，参数a与进气值的倒数之间的相关系数R2=0.999，说明参数a与进气值的倒数之间具有很好的线性相关性。通过数据拟合，得到参数a与进气值ψa之间的关系式为:

拟合曲线如图3-11所示。

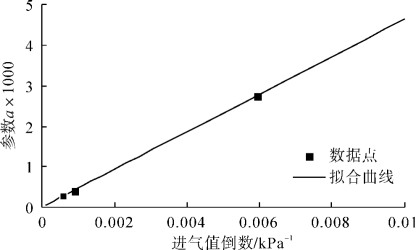
图3-11　参数a与进气值ψa的关系

图3-12为参数n随干密度变化的情况。在VG模型中，参数n与曲线的斜率相关。从图上可以看出，随着干密度增大，参数n也增大，且参数n与干密度之间具有较好的线性关系。通过曲线拟合，得到参数n与干密度之间的关系式:

相关系数R2=0.999。

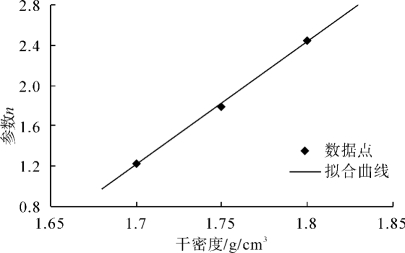
图3-12　参数n随干密度的变化