土壤水的运动主要是指液态的流动。在一定条件下,土壤水也可以气态形式流动。液态水的流动可以在饱和状态下流动,也可以在非饱和状态下流动。目前,在设计路基时,对路基的湿度控制标准是使路基始终保持在干燥或中湿状态,因此,路基土多处于非饱和状态,路基中水的运动则属于非饱和流问题。
饱和流和非饱和流各具自身的特点。就水分流动的驱动力而言,饱和流为重力势梯度和压力势梯度;而非饱和流的驱动力为基质势梯度和重力势梯度。就导水率而言,饱和流的导水率为一常数,而非饱和流的导水率则是基质势和含水量的函数。尽管非饱和流和饱和流之间存在着差异,但就水流而言,它们都服从于达西定律。
(1)非饱和土达西定律
处于非饱和状态下的土壤水和饱和土壤水一样,也遵循热力学第二定律,水分从水势高处自发地向水势低处运动。一般认为,适用于饱和水流动的达西定律在很多情况下也同样适用于非饱和土壤水分流动。
最早将达西定律引入非饱和土壤水流动的是Richards。非饱和流动的达西定律可表示为:
![]()
虽然上式的形式与饱和流动的达西定律相同,但水势和导水率却有不同的含义和特点。
首先,饱和土壤水和非饱和土壤水的运动尽管都是由于水势差的存在而引起的,但对于饱和土壤水,任一点的土水势ψ包括重力势ψg和压力势ψp,它们分别由该点相对参考平面的高度和地下水位以下的深度来确定。对于饱和土壤水,习惯上用水头h表示水势ψ,即总水头等于位置水头和压力水头之和,水由总水头高处向总水头低处流动。对于非饱和土壤水,当无须专门考虑溶质势ψs、温度势ψt以及压力势ψp时,任一点的土水势只包括重力势ψg和基质势ψm。若以单位重量的土壤水计,水势单位用水头表示,那么,非饱和土壤水的总水头就等于位置水头与基质势水头(或称负压水头)之和。前者取决于相对参考平面的高度,后者取决于土壤的干湿程度。对于非饱和土壤水,不能笼统地说水由位置高处流向位置低处,或水由湿处移向干处,流动遵循的唯一原则是自土水势高处向土水势低处运移。
其次,非饱和土壤水流动和饱和土壤水流动的另一重要区别在于导水率。当土壤处于饱和状态时,全部孔隙都充满了水,因而具有较高的导水率值,且为常数。非饱和土壤的导水率K又称为水力传导度,由于土壤中部分孔隙为气体所填充,故其值低于该土壤的饱和导水率。不仅如此,非饱和土壤水的导水率K还是土壤水基质势或含水率的函数,记为K(ψm)或K(θ)。
(2)非饱和土壤水运动基本方程
达西定律是多孔介质中流体流动所应满足的方程。质量守恒是物质运动和变化普遍遵循的原理,将质量守恒原理具体应用在多孔介质中的流体运动即为连续方程。达西定律和连续方程相结合便导出了描述土壤水分运动的基本方程。
研究只限于固相骨架不变形的多孔介质。设在土壤水分流动的空间内任取一点(x,y,z),并以该点为中心取无限小的一个平行六面体。六面体的边长分别为Δx,Δy,Δz,且和相应的坐标轴平行,如图2-5所示。
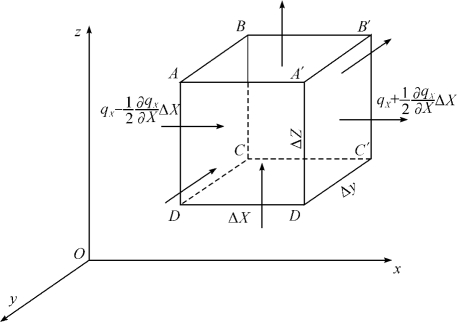
图2-5 直角坐标系中的单元体
现分析自t至t+Δt时间内单元体的水体质量守恒问题。设单元体中心土壤水分运动通量在3个方向上的分量分别为qx,qy,qz,水的密度为ρw。取平行于坐标平面yoz的两个侧面ABCD和A'B'C'D',其面积为ΔyΔz。自左边界面ABCD流入的土壤水分通量为qx- ,在Δt时间内由此界面流入单元体内的土壤水质量为:
,在Δt时间内由此界面流入单元体内的土壤水质量为:

自右边界面A'B'C'D'流出的土壤水分通量为qx+![]() ,在Δt时间内由此界面流出单元体内的土壤水质量为:
,在Δt时间内由此界面流出单元体内的土壤水质量为:
![]()
因此,沿x轴方向流入单元和流出单元体的土壤水分质量之差为:
![]()
同理,可以写出沿y轴方向和沿z轴方向流入单元体和流出单元体的土壤水分质量之差分别为- ΔxΔyΔzΔt和-
ΔxΔyΔzΔt和-![]() ΔxΔyΔzΔt,这样,在Δt时间内流入和流出单元体的土壤水分质量差总计为
ΔxΔyΔzΔt,这样,在Δt时间内流入和流出单元体的土壤水分质量差总计为
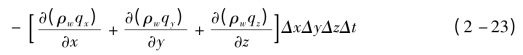
在单元体内,土壤水分的质量ρwθΔxΔyΔz,θ如前为体积含水率。由于固相骨架不变形,即Δx,Δy,Δz不随时间改变。根据质量守恒原理的物理意义,在单位时间内净入流量(或净流出量)必与土体内变化的含水量相等。因此,Δt时间内单元体内土壤水分质量的变化量为

单元体内土壤水分质量的变化,是由流入单元体和流出单元体的水分质量之差造成的。根据质量守恒原理,两者在数值上是相等的,由此可得出土壤水分运动的连续方程为:
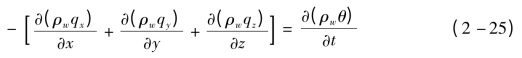
或表示成(https://www.daowen.com)
![]()
∇·(ρwq)或记为div(ρwq),称为(ρwq)的散度。当土壤水不可压缩时,水的密度为常数,此时连续方程可写为
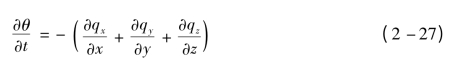
或

将式(2-19)表示的达西定律代入上式,即可得出非饱和土壤水分运动的基本方程
![]()
上式可展开为

设土壤为各向同性,则Kx(θ)=Ky(θ)=Kz(θ)=K(θ)。对于非饱和流动,总水势ψ由重力势ψg和基质势ψm组成。取单位重量土壤水分的水势,则ψ=ψm±z,将此关系代入到式(2-30)后可得
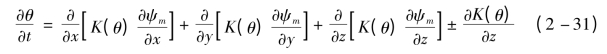
式(2-31)便是非饱和土壤水分运动的基本微分方程式。由于导水率是基质势ψm或含水率θ的函数,故此方程为一个二阶非线性的偏微分方程。除少量问题外,一般情况下此方程解析求解是困难的,大量的问题需用数值法求解。
(3)基本方程的各种形式
运用基本方程解决实际问题时,遇到的情况是各式各样的。有的土壤剖面可近似为均质土壤,有的则须视为层状土壤;有的土壤剖面须考虑地下水位的存在和变化,有的则可视为无地下水位;有的土壤水分运动可近似为一维或二维(平面)的流动问题,对此宜用直角坐标系,有的则可近似为轴对称流动问题,宜用柱坐标系,如此等等。为了适用于复杂多变的实际问题,并使得问题的分析比较简便,故将基本方程转换为其他的形式。基本方程的转换有多种形式,本书根据道路工程的实际情况和特点,仅介绍以含水率θ为因变量的基本方程。
定义非饱和土壤水的扩散率D(θ)为导水率K(θ)和比水容量C(θ)比值,即
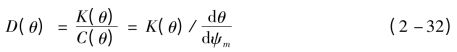
显然,非饱和土壤水的扩散率D同样是土壤含水率θ或基质势ψm的函数,其函数关系必须通过试验测定。
引入扩散率后,利用复合求导则有
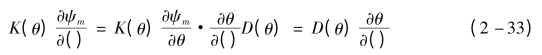
至此,非饱和流动的达西定律可表示为以下形式:
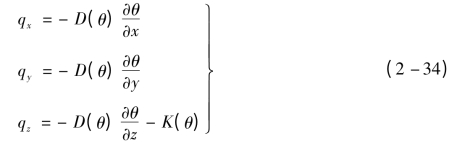
同理,由基本方程(2-31)可改写出以含水率θ为因变量的土壤水分运动的基本方程
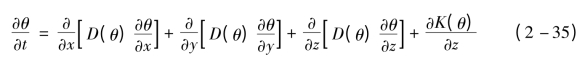
以上是非饱和土壤水分运动基本方程改换为以含水率θ为因变量的基本方程。
本书主要考虑含水量在路基横断面的分布情况,所研究的水分迁移是二维的,因此二维水分迁移的基本方程为:
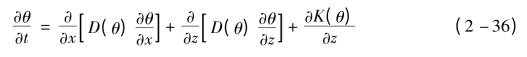
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






