非饱和土与饱和土的不同之处在于，非饱和土中存在基质吸力的作用。Croney［53］首先认识到基质吸力对非饱和土力学性能的重要影响。Fredlund［54］提出，非饱和土的体积和含水量变化可以用两个应力状态变量的函数来表示，即平均净应力［p=(σ1+σ2+σ3)/3-ua］和基质吸力(s=ua-uw)，非饱和土的性能可以通过平均净应力和基质吸力的变化来描述。非饱和土有3个主要的本构关系:

1)总体积和含水量方面:表示净应力和基质吸力与土体的体积和含水量的关系;

2)剪切强度方面:表示土体的剪切强度与应力状态变量之间的关系;

3)水力传导参数方面:表示土体的水力传导参数与应力状态变量之间的关系。

在目前大部分的计算分析中，对于非饱和土渗流、体积变化和剪切强度问题通常都是相互独立考虑的。实际上，许多岩土工程问题都应该进行渗流、变形和剪切强度的耦合分析，那么，必须建立以上的3个本构关系。基于当前的计算能力，剪切强度和水力传导本构关系都可以通过土-水特征曲线间接得到，而土-水特征曲线是体积-质量本构关系中的一部分，可见，体积-质量本构关系是非饱和土耦合分析中的关键问题。鉴于非饱和土体积-质量本构关系的重要性，近几十年来，国内外不少学者进行了这方面的研究。

通常情况下，采用孔隙比e和含水量w作为土体的总体积和水相体积的状态变量，建立孔隙比e和含水量w与净应力(σ-ua)和基质吸力(ua-uw)的关系。将e-(σ-ua)-(ua-uw)和w-(σ-ua)-(ua-uw)的关系在三维坐标系下表示的曲面称为非饱和土体积-质量本构面［55］。

Fredlund and Rahardjo［55］通过一系列的、按照一定应力路径进行的试验给出了典型的体积-质量本构面，如图1-1所示。由于进行非饱和土试验条件有限、费用较高且耗时较长，建立非饱和土的体积-质量本构模型是很有必要的。

图1-1　典型的体积-质量本构面［55］

Alonso et al［56］认为土体在一定吸力下的压缩曲线与饱和状态下的压缩曲线是相似的，即在一定吸力下的非饱和土压缩曲线可以近似由两条直线来表示，这两条直线的交点即为土体的屈服应力，其中加卸载压缩曲线的斜率是一个常数，不随吸力的变化而变化，即有κ(0)=κ(ψ);而原始压缩曲线的斜率是吸力的函数，即有λ=λ(ψ)。Wheeler and Sivakumar，Tang and Graham，Blatz and Graham，Chiu and Ng，Lloret et al，Tamagnini等［57-62］的体积-质量本构模型中也采用了这种假设。但对于λ与吸力之间的关系还存在一定的争议，Alonso et al［56］认为λ随着吸力的增大而增大，而Wheeler and Sivakumar［57］认为λ随着吸力的增大而减小。

Fredlund，Fredlund and Morgenstern，Richards et al，Ho，Alonso et al，Fredlund and Rahardjo，Ho and Fredlund等［55-56，63-67］通过试验研究了土体在一定净应力下相对于吸力的压缩曲线，试验结果如图1-2所示。结果表明，土体在一定净应力下相对于吸力的压缩曲线与相对于净应力的压缩曲线具有相似性。Fredlund and Rahardjo［55］提出了对土体相对吸力的压缩曲线与相对于净应力的压缩曲线的假设比较，如图1-3。比较结果表明，当土体的吸力小于土体的进气值时，相对于吸力的压缩曲线与相对于净应力的压缩曲线是一样的;当吸力大小于土体的进气值时，吸力引起的土体结构体积变化是很小的;当吸力大于土体的残余吸力后，吸力的变化基本上不引起体积的变化。Alonso et al［56］认为土体在一定净应力下相对于吸力的压缩曲线可以近似由两条相交于屈服吸力的直线表示，相对于吸力的加卸载压缩曲线和原始压缩曲线的斜率分别为κs和λs，且κs和λs与净应力不相关。

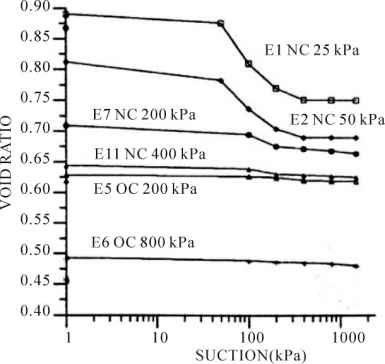
图1-2　孔隙比随吸力的变化曲线［65］

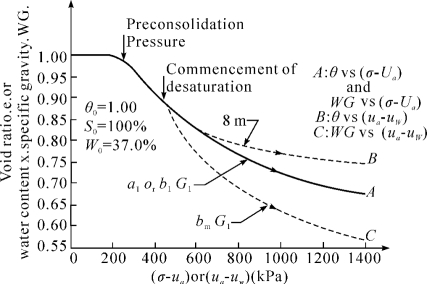
图1-3　初始饱和土体相对于吸力的压缩曲线与相对于净应力的压缩曲线的比较［55］

S.K.Vanapalli，Charles W.W.Ng，Lai Chunhon，Ho Mei Yung，Zhou Jian，龚壁卫，苗强强和周冬等［68-75］通过室内试验得到了不同应力状态下的土-水特征曲线，分析了应力对土-水特征曲线的影响。Sharma［76］通过试验研究了在一定吸力下含水量对非饱和土压缩性的影响，结果表明，在一定的吸力下，含水量越大，土体的压缩性越大。Wheeler［77］认为土体的含水量和孔隙比之间存在一定的关系，并提出了一个类似于土体总体积的预测含水量的弹塑性模型。

Fredlund［78］提出了一个非线性弹性模型，认为非饱和土孔隙比本构面在很大范围的对数应力变量下是线性的。在任何应力状态下，孔隙比e和含水量w可以按下式计算:

式中:e0，w0——分别为初始孔隙比，初始含水量;

Ct——相对于净平均应力的体积变化指数;

Cm——相对于基质吸力的体积变化指数;

(σ-ua)0，(ua-um)0——分别为初始净平均应力和初始基质吸力;

Dt——相对于净平均应力的含水量指数;

Dm——相对于基质吸力的含水量指数。

其中，参数Ct、Dt均是土体吸力的函数;参数Cm、Dm分别为净平均应力的函数。

Kayadelen C.［79］通过对压实土进行几组常吸力下的固结试验以及常竖向净应力的压力板试验，分析了孔隙比和含水量随净应力和基质吸力的变化特征，并基于试验数据，建立了Ct、Dt与基质吸力之间以及Cm、Dm与净应力之间的指数关系式。

Ho［80］认为在一定的孔隙比下，净平均应力与土体吸力之间呈线性关系。孔隙比曲面在半对数坐标系中，可以近似地画成3个平面，分别称为平面Ⅰ、Ⅱ和Ⅲ。这3个平面相交于应力状态变量均为零时在孔隙比(如lg(σ-ua)=0且lg(ua-uw)=0)纵坐标上的点。平面Ⅰ垂直于e-lg(σ-ua)平面，平面Ⅲ垂直于e-lg(ua-uw)平面，平面Ⅱ表示平面Ⅰ和平面Ⅲ之间的过渡。平面Ⅱ与e-lg(σ-ua)平面和elg(ua-uw)平面均相交。这个曲面的3个平面，平面Ⅰ、Ⅱ和Ⅲ可以用下式表示:

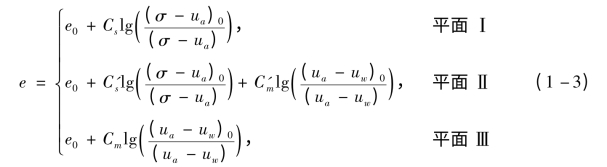(www.daowen.com)

式中:e0——初始孔隙比;

(σ-ua)0——初始净平均应力;

(ua-uw)0——初始基质吸力;

Cs——平面Ⅰ与e-lg(σ-ua)平面的交线的斜率;

Cm——平面Ⅲ与e-lg(ua-uw)平面交线的斜率;

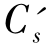——平面Ⅱ与e-lg(σ-ua)平面交线的斜率;

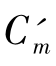——平面Ⅱ与e-lg(ua-uw)平面交线的斜率。

Lloret and Alonso［81］提出了多种体积质量本构面的曲面拟合方程。Lloret and Alonso认为，当施加一定范围的总应力时，孔隙比本构面可以用下式来表示:

式中:e——孔隙比;a，b，c，d——曲面拟合参数。

如果应力变化范围很大，Lloret and Alonso(1985)建议了一个更合适的孔隙比曲面方程:

式中:e——孔隙比;a，b，c，d——曲面拟合参数。

除了上面两个描述孔隙比本构面的方程式，Lloret and Alonso也提出了饱和度本构面方程式:

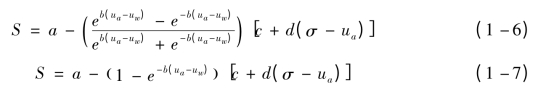
式中:S——饱和度;a，b，c，d——曲面拟合参数。

Hung［82］认为在一定孔隙比下，吸力与净平均应力的关系可以用斜率为ξ的直线表示。孔隙比曲面可以表示成:

式中:e0——初始孔隙比;

Ps——膨胀压力;

Cs——膨胀指数。

Pereira［83］采用了一个5参数函数来拟合孔隙比和基质吸力的关系，该关系式为:

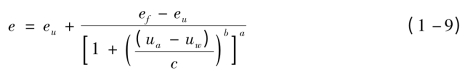
式中:eu——初始孔隙比;

ef——最终孔隙比;

a——控制函数对称性的参数;b——控制斜率的参数;c——拐点对应的吸力值。

综上所述，对于非饱和土，净应力和基质吸力的变化均会对土体的孔隙比和含水量产生显著影响，研究孔隙水和含水量与净应力和基质吸力的关系是非饱和土本构关系的重要内容。目前，国内外已有不少学者对非饱和土的体积-质量本构关系进行了研究，并提出了孔隙比和含水量与净应力和基质吸力的关系，但基本上都是基于一定的假设基础之上，或者是根据某种土体的试验数据建立的，因而到目前为止，还没有得到被学术界广泛认可的体积-质量本构关系。因此，对于非饱和土的体积-质量本构关系，有待于进一步的研究。