在潜水含水层中抽水时，潜水面是一个随时间不断变化的曲面。因此，地下水向潜水井的非稳定运动与承压含水层中的非稳定运动有显著的不同，主要表现为：

（1）抽水井附近地下水流具有三维流的特征。

（2）潜水井的导水系数T=K·h是随时间和距离而变化的。

（3）具有“迟后疏干”（延迟给水）现象。含水层储存量的释放主要是以重力排水的形式，在水位下降后，含水层的疏干不是瞬时完成的，而是缓慢排水，逐渐释放水量。这种现象称为迟后疏干现象。沃尔顿在20世纪60年代初提出潜水井抽水时降深—时间曲线有3个不同的区段。

抽水初期，S-t曲线与承压井的泰斯曲线一致。这时主要为弹性释放，可用贮水系数表示。虽然潜水位下降了，重力疏干因滞后反应所起的作用还很小。所以，含水层的作用相当于贮水系数小的承压含水层。这阶段的时间很短，也许只有几分钟。

抽水中期，S-t曲线的变化很像有越流补给时半承压含水层的情况，明显偏离泰斯曲线，曲线斜率变小，甚至出现短时间的假稳定。此时重力疏干的作用逐渐明显，贮存的重力水逐步释放出来，起到连续再补给的作用。弹性释放的作用依然存在，但所占比例已逐渐减弱，此时给水度的数值逐渐增大而趋向潜水含水层的最大值。这个阶段，由于潜水层性质的不同，可能是几分钟，也可能是几天。

抽水后期，S-t曲线又与泰斯曲线相一致，水头下降速度增大，降落漏斗扩展，这时主要为重力疏干作用。由于抽水时间的增长，重力排水已跟得上水位的下降，滞后作用可忽略不计，此时的给水度达到最大值。

由于潜水向井运动时水流情况十分复杂，迄今尚无严格的、确切的解。目前仅有一些近似的解法，以及考虑上述三问题中某一个或两个问题的解。

（一）仿泰斯公式

（1）以Sw表示抽水井中的水位降深，当时，即可认为水位降深与潜水含水层厚度h0相比很小，可忽略不计，则式（4-76）及式（4-78）可分别写成

即此时可直接将承压含水层的泰斯公式近似用于潜水层的计算。

（2）当时，考虑导水系数变化，在利用泰斯公式时，水位降深值需要按下式进行修正：

于是潜水的泰斯公式可以写成

潜水的雅各布公式可以写成

（二）考虑潜水含水层滞后疏干的博尔顿公式

博尔顿公式的水文地质模型为：(www.daowen.com)

（1）潜水含水层在整个影响带内是均质、各向同性及等厚的。

（2）含水层侧向无限延伸。

（3）底板为水平的隔水层。

（4）井是完整单井，井半径可以忽略，定流量抽水。

（5）水的释放不是瞬时的，抽出的水量由两部分组成，即：1）由于水位下降所引起的含水层的弹性释放量，这是释放瞬时完成的；2）由于含水层厚度减薄所引起的重力疏干量，这些水量的释放是缓慢的释放过程，不是瞬时完成的。

博尔顿在上述前提条件下导出了抽水开始后t时刻，距抽水井r处的水位降深值的计算式

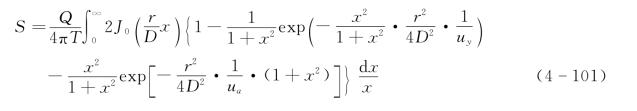
以代表其积分值，则式（4-101）为

称为潜水含水层的完整井的井函数，标准曲线如附图3所示，它描述的S-t曲线是一条横的S形状的曲线。可将式（4-102）分解为3部分

式（4-101）～式（4-105）便是博尔顿公式。利用它们可预测潜水井任一点处任一时刻潜水位的水位降深，或根据抽水试验资料用以确定含水层的有关参数。前者是根据给定的数值查图表进行计算的问题，比较简单。下面着重介绍确定含水层参数的问题。解决该问题通常采用配线法，其基本原理同前。主要计算步骤如下：

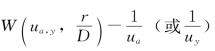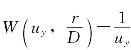（1）具备一张标准曲线图，见附图3。它由两类曲线组成：位于值左侧称为A类标准曲线，为标准曲线束。值右侧的称为B类标准曲线，为标准曲线束，A类标准曲线的右边部分及B类标准曲线的左边部分都接近于水平渐近线。A类标准曲线用于解释潜水含水层抽水初期的资料，B类标准曲线用于分析抽水后期的资料；

（2）在与标准曲线图模数相同的透明双对数纸上点绘S-t实测曲线；

（3）将S-t曲线重叠于标准曲线图（附图3）上，保持坐标轴平行，使S-t曲线尽可能多地与某一个的A组曲线重合，任选一配合点，读得，代入式（4-105）求T、μ*；

（4）将S-t曲线后面部分尽可能多地与同的B组曲线组合，任选一配合点，读得，代入式（4-105）求T、μ。

两次计算（早期和后期）得T值应相等或相接近。根据求得的值，计算滞后指数值：

滞后指数近似看成是常数，是个经验数值，其物理意义仍然不明确，在同一次抽水试验中，根据与抽水井距离（r）不同的观测孔的水位数据计算出的数值不同。所以“滞后指数”的数值可靠性较差，因而使博尔顿理论的应用受到一定影响。