实际上，任何地区的含水层分布范围都是有限的，只是当抽水井离边界较远，尤其是抽水时间延续不长时，含水层才能近似视为无界的。

有界含水层是指含水层的侧向有隔水边界或供水边界。研究有界含水层中地下水向承压完整井的运动，是以泰斯单井公式为基础，利用映射原理及叠加原理进行的。

映射原理就是把边界当作一面“镜子”来映射实际存在的井（实井），在“镜”内（即边界的另一侧）对称位置上成像得一虚构的井（虚井），以虚井代替边界的作用。于是，就把有界含水层中井的计算问题转化为无界含水层中干扰井群的计算问题。为了保证映射后按干扰井群所得的结果完全等同于有边界时所得的结果，映射应满足以下要求：

（1）实井与虚井的位置对称于边界。

（2）实井与虚井的工作强度（抽水量或注水量）相等。

（3）虚井的工作性质取决于边界的性质，如为定水头供水边界，实井与虚井性质相反；如为隔水边界，实井与虚井性质相同。

图4-30　直线隔水边界附近的抽水井

（4）虚井与实井的结构（井径、井的类型等）相同。

（5）虚井与实井同步工作。

（一）抽水井位于直线隔水边界附近

设隔水边界附近有一抽水量为定值Q的抽水井。若在边界的另一侧，与其对称的位置上映射一抽水量相等的抽水井，用此虚构的抽水井来代替边界的作用，这就成为无界含水层中干扰井群的计算问题（图4-30）。根据迭加原理，任一点

A处的降深值为(www.daowen.com)

如果满足雅各布公式的应用条件，A点处的降深亦可写成

化简后得

式（4-88）和式（4-89）就是直线隔水边界附近完整井的水位降深公式。由式（4-89）可见，降深S和时间的对数值lgt呈直线关系，当隔水边界产生影响时，该直线的斜率。在无界含水层中S-lgt曲线的斜率。则i′=2i。利用这一特点，我们可根据抽水资料的S-lgt曲线判断水文地质条件。当S-lgt曲线的直线段出现斜率急剧变大（i′≈2i）时，可确定附近存在隔水边界，此边界可能是隔水断层，也可能是其它隔水岩体。直线段S-lgt的资料，同样可用来确定含水层的参数。

（二）抽水井位于定水头供水边界附近

当边界是一定水头供水边界时，应映射一个注水井来代替边界的作用（图4-31）。此时，任一A点处的降深应为

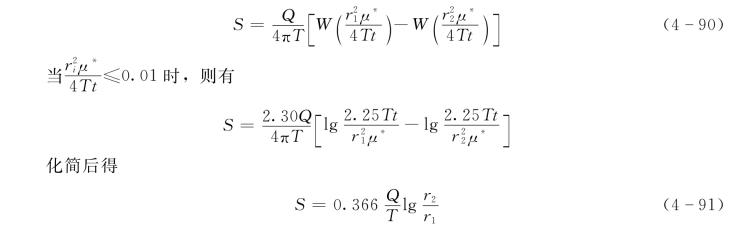
式（4-90）和式（4-91）就是直线补给边界附近完整井的水位降深方程式。在式（4-91）中，等式右边没有时间t这个变量，全部是常数项。因此S亦为常量，和稳定井流的方程式完全一致。可见在存在补给边界的条件下，抽水井工作一段时间后，渗流场便达平衡状态，水流呈稳定流动。实际上，在此条件下，井的出水量是由补给边界处的补给量来补偿的，不再消耗含水层的储存量，因此降落漏斗不再扩展，水流呈稳定运动。由此可见，在具有补给边界的情况下，含水层某一断面处的S与lgt初期呈曲线，而后期呈直线。当补给边界发生影响时，便成水平线。根据S-lgt曲线的这种特点，有助于我们利用抽水试验资料判别地下水与地表水间的水力联系情况，以及发现隐状的富水断层和富水岩体。利用S-lgt直线段同样可以确定含水层的各项水文地质参数。

图4-31　直线供水边界附近的抽水井