（一）承压含水层的弹性特征及其贮水系数

承压含水层上覆隔水顶板岩层的压力是恒定的，它由含水层的颗粒骨架和水共同承受。当从承压含水层中抽水或其它原因导致水位下降时，水承受的压力相应减少，水密度变小，水体积膨胀，释放一定数量的水。与此同时，水承受压力减小的那部分压力转由颗粒骨架承受，颗粒骨架受压增大，粒间压密，含水层压缩，释放一定数量的水。若水头升高，则引起相反的效应。总之，承压含水层随其水头的增减，引起弹性释水或贮水。例如，从规模较大的承压含水层中抽水时，当缺乏补给时，就是在不断消耗弹性贮存水量的过程，因而是一个非稳定运动的过程。

不同岩性、不同结构的承压含水层，弹性释水或贮水的能力也不同。为便于比较和计算，用弹性释水（或贮水）系数作为参数指标。弹性释水系数定义为：当水头降低（或升高）一个单位时，从水平面积为一个单位面积，高为含水层厚度的含水层柱体中所释放（或贮存）的水量。弹性释水系数用符号μ*表示，无量纲。一般承压含水层的μ*值介于10-5～10-3之间。

（二）承压完整井的非稳定运动基本微分方程

在承压含水层中打一口完整单井，以定流量Q抽水，水量来自含水层弹性贮量的瞬时释放，井径无限小。假定含水层的平面上无限延伸、均质、各向同性且水平埋藏；抽水前的水头面水平，水头为H0。渗流服从达西定律。抽水后将形成以井轴为对称轴的降落漏斗（图4-27）。

为方便起见取柱坐标系，原点设置在含水层底板抽水井中心处，取井轴为水头H坐标，向上为正；沿含水层底板为r坐标。

取半径为r和r+dr的两个直圆柱面所围成的环状柱体作为均衡单元（图4-27）。抽水时，在均衡时段dt内，通过半径为r的断面流出均衡单元的水量为Qrdt；通过半径为r+dr的断面流入均衡单元的水量为dt；由于抽水，均衡单元内的水头下降，这时单元内含水层将释放一定体积的水量dV贮。

根据水均衡原理，在均衡时段dt时间内有

图4-27　轴对称二维非稳定井流

化简得

由于渗流服从达西定律，则Qr可表示为

为r处过水断面上的水力坡度。忽略不计K及M变化的影响，视K和M沿r方向为常量。则有

其弹性释放量

其中为均衡时段内水头随时间的变化率。

将式（4-69）和式（4-70）代入式（4-67）中，得

化简后有

令T=KM，式（4-71）又可写为

式中　T——导水系数，m2/d。

若以H0表示抽水前的水头，S=H0-H即为降深，则式（4-72）亦可写为

T与μ*均为承压含水层的水文地质参数。由达西定律可知，导水系数在数值上等于水力坡度为1时通过整个含水层厚度的单宽流量。

式（4-72）与式（4-73）即为承压完整井的非稳定运动基本微分方程。

（三）数学模型、定解条件及其解

1.数学模型

上面所讲的承压完整井非稳定流运动基本微分方程是以水均衡原理和达西定律为基础指导出来的水头与空间和时间的一般表达形式，该式反映了地下水运动所服从的普遍规律。为了确定实际问题的地下水运动规律，必须针对实际问题给方程式一定的附加条件，组成数学模型再求解。这个附加条件是初始条件和边界条件，初始条件和边界条件统称为定解条件，也就是说数学模型是由偏微分方程加定解条件组成的。

2.初始条件

对研究稳定流来讲，基本的偏微分方程再加上与之相应的边界条件就构成了一个完整地描述地下水运动的数学模型。对非稳定流还要加上初始条件。所谓初始条件，就是给定某一时刻渗流区域上的水头分布，以便指明非稳定过程是从何种状态下开始研究的。需要指出的是“某一时刻”系相对时刻，常把这一时刻认为是零时刻，即t=0。

3.边界条件

边界条件系指渗流区域几何边界上的水力性质。通常分两类：第一类边界条件与第二类边界条件。第一类边界条件又叫做给定水头边界条件（供水边界）。与含水层系统联系畅通的地表水体（如河流及湖泊）相接处就是典型的第一类边界，其水位可作为第一类边界条件的值。在地下水溢出带处，地下水头取决于地面标高，只要溢出带不消失，溢出带就是第一类边界，其地面标高就可以作为第一类边界条件的值。在理论上，第一类边界具有无限补给或排泄地下水的能力。第二类边界条件又叫做给定流量边界条件（隔水边界）。最典型的第二类边界是隔水断层和固定的地下水分水岭所确定的流量为零的边界，以及抽水井构成的以井壁为边界的定流量边界。

4.数学模型的解算方法

常用的数学模型的解算方法主要有两种。

（1）解析解法。就是用数学物理方法，诸如分离变量法、拉普拉斯变换、傅立叶变换、汉克尔变换等方法求解数学模型，从而得到一个能反映含水层系统中某些变量变化规律的解析表达式，这种表达式称为解析解或分析解。由于解析解可以将描述地下水运动的各种物理量，例如水头（或降深）、水量及各种参数反映在一个表达式中，这样就可以利用数学分析的方法来研究各个量之间相互联系与相互制约的内在规律。因此，在可能的情况下，应尽量去求模型的解析解。由于用解析解法解数学模型所必须的假设条件常常受到相当大的限制，例如含水层一般须是均质的，边界的几何形状不能是任意的等，这就使得许多数学模型难以用解析解法求解。即使对定解条件作了相当的概化假设，往往也因解析解法中包含着复杂的积分项及一些特殊函数而限制了解析解法的应用。限于篇幅这里只介绍解析解法。

（2）数值解法。通常使用的主要是有限差分法与有限单元法。不论哪种解法，其基本步骤是一样的，都是通过以下三步解决问题的：

1）将渗流区域按一定的规律剖分成许多（例如几个）小的子区域（又叫单元），将边界的不规则几何形状依一定规律裁弯取直，把非均质的含水层按子区域均质化，按特定要求在子区域上定义一个点称为结点（或叫点元），然后把整个渗流区域上的连续水头分布离散化为在全部结点上由几个数所组成的数组；

2）在离散化的基础上，将偏微分方程联同边界条件转化为线性代数方程组；

3）解线性代数方程组求出水头分布。若为非稳定流，还应根据初始水头分布多次解线性代数方程组，以求得各时刻的水头分布。

在把偏微分方程转化为线性代数方程组时，有限差分法是采用差商来代替导数，而有限单元法则是利用线性的或高次的插值函数来实现离散化，然后用变分方法或其他数学方法将偏微分方程转化为线性代数方程组。随着电子计算机的发展，数值解法已成为求解地下水运动数学模型的重要方法，限于篇幅这里不作介绍，详细内容可参考有关地下水动力学教材。

（四）泰斯公式

根据将上述假定解条件与微分方程式（4-72）相结合，得下列数学模型：

泰斯给出了这一问题的解（解法可参考地下水动力学）

式中　u——参变量，；

　　　——指数积分，可用收敛级数表示为

在地下水动力学中，上述指数积分又称为泰斯井函数，用W（u）表示，即

上式的值可利用表4-7查得。将W（u）代入式（4-74）中，并用降深S表示，则得

式（4-74）及式（4-76）均称为泰斯公式。

从泰斯井函数的级数展开式可以看出，当u值足够小时，级数第三项以后的各项数值都非常小，W（u）可用级数的前两项近似表示：

若将代入上式，得

于是泰斯公式又可近似表示为

(www.daowen.com)

式（4-77）与式（4-78）又称为雅各布公式。

u取不同数值时，雅各布公式与泰斯公式比较，其误差值如下：当u≤0.01时，误差≤0.25%；u≤0.05时，误差≤2%；u≤0.1时，误差≤5%。

（五）泰斯公式应用

1.泰斯公式和雅各布公式通常可作某些计算

在含水层参数T、μ*以及井的抽水量Q给定的情况下，可直接利用泰斯公式，确定井中或含水层中任一点处任一时刻的降深值，从而可以预测抽水时降落漏斗的发展规模及变化趋势。当含水层参数下，μ*以及抽水的时间t和降深S给定时，还可以确定井的抽水量。

【例4-2】 有一侧向无限分布的承压含水层，其导水系数T=2000m2/d，贮水系数μ*=2×10-4。有一完整生产井以抽水量Q=3140m3/d进行开采。试计算距井300m处，开采10d、20d、30d时的降深。

【解】 利用泰斯公式计算：

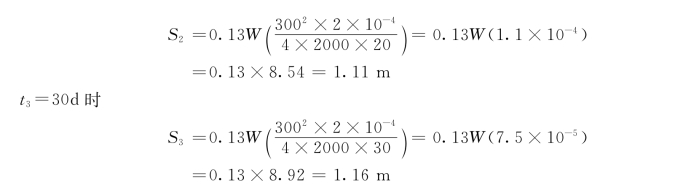
2.根据单井非稳定抽水试验资料确定含水层的参数

确定含水层参数的方法较多，目前常用的方法有配线法及直线图解法。

（1）配线法。此法是一种通过实测数据与理论曲线进行配线以确定含水层参数T和μ*值的图解—解析法。由于所采用的实测资料不同可分为降深—时间配线法，降深—距离配线法及降深—时间距离配线法。由于上述3种方法的图解原理和计算步骤基本相同，因此，仅以降深—时间配线法为例进行讨论。

现将泰斯公式

取对数，得

在式（4-79）和式（4-80）中，对某一观测孔而言均为常数。所以在对数坐标系中W（u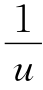）-曲线和S-t曲线形状相同，只是纵坐标和横坐标平移了的距离。因此，只要将两线重合，两重叠坐标系上任意一点均满足式（4-79）和式（4-80），即满足泰斯公式。

由以上讨论可得到确定参数的方法及步骤：首先在双对数坐标纸上用表4-7中所列的数据绘制W（u）-曲线，此曲线常称为标准曲线或理论曲线（见附图1）。在与绘制理论曲线相同模数的双对数坐标纸上，取纵坐标为S，横坐标为t，用抽水试验资料绘出降深历时曲线。在保持各对应坐标轴互相平行的前提下，移动二坐标纸，使实测降深历时的数据点均匀地落在理论曲线的两侧。任选一点，在两张相重合的双对数坐标纸上取其四个坐标：W（u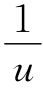）、、S和t，为简化计算，尽可能选取W（u）及为10的整数次幂的点。然后根据下式确定T和μ*：

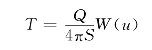
配线法的主要优点是，能较充分地利用实测数据，减少观测误差的影响。尤其当实测的降深曲线偏离泰斯公式而服从其他公式时，就可在图上直观地看出来。配线法的不足之处是，当实测的降深值变化不大时，会给配线带来很大的随意性，影响计算结果的精度。

【例4-3】 某地区打一承压完整井进行非稳定抽水试验，承压含水层由均粒细砂组成，平面上无限延伸，抽水量为542.4m3/d，距井110m处有一观测孔，观测资料见表4-8。试用配线法求贮水系数和导水系数。

表4-8　抽水试验实测资料

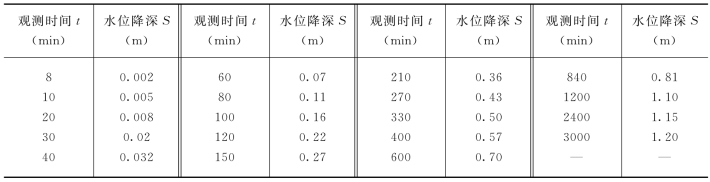
【解】 解题步骤如下：

（1）在与标准曲线模数相同的透明双对数纸上，将表4-8中的S、t资料点绘成实测曲线；

（2）将透明实测曲线纸蒙在标准曲线上（附图1），保持相应坐标轴S轴与W（u）轴，t轴与轴平行，移动透明双对数坐标纸，取得最佳配合，如图4-28所示；

（3）取配合点A，读出两张曲线图上的4个坐标值为

（4）求含水层参数，将上述数值代入公式计算得

（2）直线图解法。该法是根据实测的降深历时数据点在半对数坐标纸上展成的直线部分，通过图解计算以确定参数T和μ*。由于所依据的实测数据不同，直线图解法可分为降深—时间直线图解法、降深—距离直线图解法及降深—时间距离直线图解法。上述3种方法的图解原理和计算步骤基本相同，因此仅以降深—时间直线图解法为例进行讨论。

可将雅各布公式

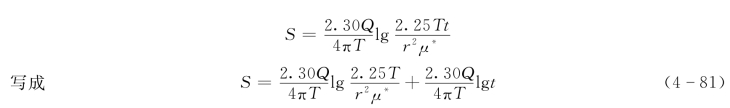
由于式（4-81）中的Q、T、μ*及r（对某一孔）皆为常数，因此S与lgt在以S为纵轴、t为横轴的半对数坐标系上为一直线。由式（4-81）知该直线的斜率：

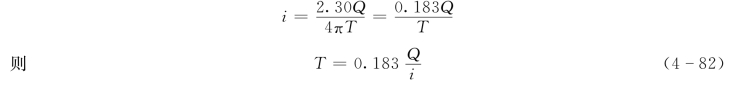
首先在以S为纵轴（普通坐标）、t为横轴（对数坐标）的半对数坐标系上，绘制降深历时曲线。然后确定曲线的直线段及其斜率i值。i值可用直线段上任意两点的坐标，按下式计算：

常用的方法是在对数坐标轴上任取一个对数周期，使Δlgt=1，则i=ΔS。将所得的i值代入式（4-83），即可求得T值。

图4-28　降深—时间配线法图示

图4-29　实测S-lgt曲线

为了计算μ*值，将直线段延长，与横轴相交得t0值。将t0值代入雅各布公式，显然有

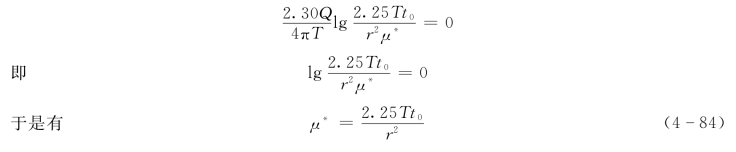
直线图解法具有作图和计算简便的优点。但由于受u≤0.01条件的限制，常使某些数据点，特别是抽水时间短的数据点或距抽水井远的观测孔的数据点偏离直线段而无法利用。

【例4-4】 用例4-3的资料，由直线图解法求参数T、μ*。

【解】 用表4-8中的资料，在单对数纸上绘制S-lgt曲线图（图4-29）。该曲线前部较弯曲，后面部分的点可近似取一直线，在直线取t=500mm及t=5000mm时的一个对数周期，这时i=0.96并代入式（4-83）求得T

延长直线与S=0的横轴相交，得交点t0=92min，代入式（9-18）求得μ*

与配线法相比，两种计算结果很相近。

（六）承压完整干扰井群的非稳定流计算

地下水向干扰井群非稳定运动的计算公式，是以单井的泰斯公式为基础，根据叠加原理来建立的。

设任意分布的n个承压完整井，均以定流量抽水，各井的抽水量分别为Q1、Q2、…、Qn。现计算在n个井共同作用下，某一时刻在任一点A处产生的降深S（图4-18）。

当各井单独抽水时，在A点处所产生的水位降深值根据泰斯公式分别为

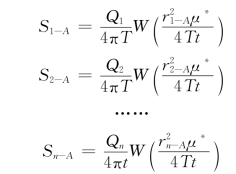
根据叠加原理，任一点A处的降深值为

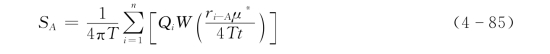
当时，可用雅各布公式叠加表示

式中　S1-A，S2-A，…，Sn-A——各井分别对A点所产生的水位下降值；

　　　Q1，Q2，…，Qn——各井的抽水量；

　　　r1-A，r2-A，…，rn-A——各井至A点的距离；

　　　t1，t2，…，tn——各井从各自开始抽水时起到计算时刻的抽水延续时间。

式（4-85）～式（4-87）为定流量抽水时，地下水向承压完整干扰井群的非稳定渗流方程。

式（4-85）～（4-87）可用于：已知含水层的水文地质参数，给定各井的抽水量；预测任一点在抽水后任一时刻的水位下降值；或给定各井在某时刻的水位降深，以确定各井的抽水量；还可根据群井抽水资料确定含水层的水文地质参数。