以上各节所讨论的地下水向井中运动的理论计算公式，都是在一系列假设的水文地质条件下获得的，生产实际往往无法满足这些条件。对于水文地质条件复杂或勘探试验工作不足的地区，常采用流量与降深之间关系的经验公式来确定流量或降深值。其具体计算步骤如下：

（1）进行多次降深的稳定流抽水试验（至少3次），利用试验所得的流量（Q）和降深（Sw）资料绘Q-Sw关系曲线。

（2）根据Q-Sw曲线的形状确定经验公式的类型。

（3）确定经验公式中的各项系数。确定系数的方法有图解法和计算法两种。

（4）根据经验公式预测流量或降深。

目前生产中采用的经验公式有直线型、抛物线型、指数型、对数型4种。

1.直线型

直线型经验公式为

式（4-54）又称裘布依公式。式中Q、Sw分别为井的流量及相应的降深值；q为待定系数（也称单位流量）。如果在普通坐标纸上，以Q为纵坐标，Sw为横坐标作图，则该式为通过原点的一条直线，该直线的斜率为q值。如果利用最小二乘法计算q值，可按下式计算：

式中Qi，Sw，i分别表示第i次抽水试验时的流量和降深值；n为稳定抽水试验的落程数。

2.抛物线型

抛物线型经验公式为

式（4-56）又称凯列尔公式。式中a、b为待定系数。该式两端除以Q，得如下直线方程：

如果在普通坐标纸上，以Q为横坐标，S0（也称单位降深）为纵坐标作图，则该式为一直线，该直线的斜率为b值，其在S0轴上的截距为a值。如果利用最小二乘法计算a、b之值，可按下式计算：

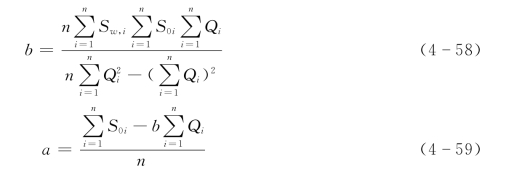
3.指数型

指数型经验公式为

式（4-60）又称斯姆列盖尔公式，式中q0和m为待定系数。将上式两端取对数则得：

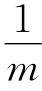如果在双对数纸上，以Q为纵坐标，Sw为横坐标作图，式（4-61）为一直线，该直线的斜率为，其在lgQ轴上的截距为lgq0。如果利用最小二乘法计算、q0之值，可按下式进行

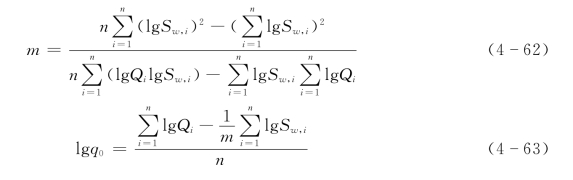
4.对数型

对数型经验公式为

式（4-64）又称阿尔托夫斯基公式。式中a、b为待定系数。如果在单对数坐标系纸上，以Q为普通坐标（纵坐标），Sw为对数坐标（横坐标）作图，式（4-64）为一直线，该直线的斜率为b值，其在Q轴上的截距为a值。如果利用最小二乘法计算a、b之值，可按下式进行

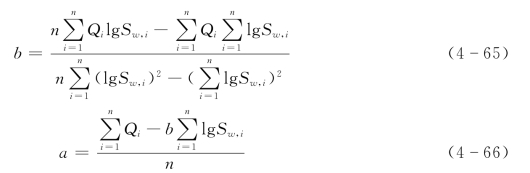(www.daowen.com)

将上述4种类型曲线归纳于表4-4中。

表4-4　流量与水位降深经验公式汇总表

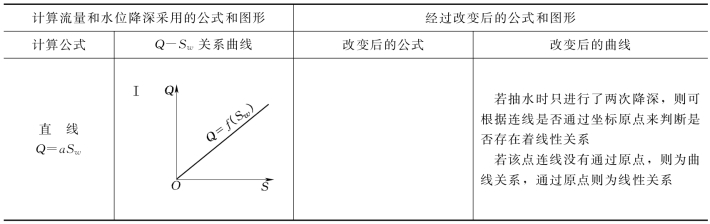
续表

经验公式是在实际试验资料基础上建立的，它反映了试验时的水动力条件和地下水的补给和消耗间的情况。若条件变化，经验公式的系数甚至公式的类型就可能产生变化。因此，通常预测的降深值不能超过试验最大降深值的1.5～2倍。

【例4-1】 在某井中进行了4个落程的抽水试验，其结果列于表4-5中，试计算当水位降深6m时的流量。

表4-5　抽水试验资料

【解】 （1）判断经验公式类型：①根据原始资料作Q=f（S）曲线（见图4-23）。呈曲线，说明不是直线类型，而可能是其它三种曲线类型中的一种；②计算S0，lgS和lgQ，列于表4-6中。作S0=f（Q），lgQ=f（lgS），Q=f（lgS）3种曲线（图4-24～图4-26）。从以上3个图可以看出Q=f（lgS）最接近直线关系，故属于对数曲线类型，即Q=a+blgS。

（2）确定待定系数a、b：

1）图解法 在图4-26中，将Q=f（lgS）直线延长，与Q轴交于一点，得截距a=50，=198.41

表4-6　计算数据表

图4-23　Q-S关系曲线

图4-24　S0=f（Q）图解

图4-25　lgQ=f（lgS）图解

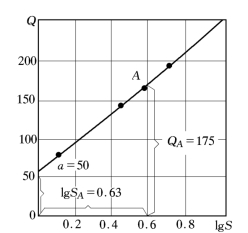
图4-26　Q=f（lgS）图解

2）最小二乘法 计算QlgSw及（lgSw）2之值，列入表4-6。可利用式（4-65）、式（4-66）计算a、b值如下：

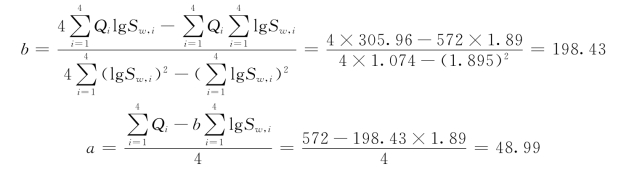
（3）计算Sw=6m时的流量：

1）图解法

2）最小二乘法

由以上计算结果可看出，图解法与最小二乘法所得结果比较接近。