在供水和排水工程中，只用单井的情况是很少的，通常总要用多个井进行抽水。在同一个水平含水层中有两个以上的抽水井同时工作，当井与井之间的距离小于两个影响半径时，就要产生相互干扰的现象。这种干扰表现为：当井中水位降深一定时，干扰井的流量比单独工作的非干扰井流量小；如果井的流量保持不变，则干扰井的水位降深要大于未发生干扰的单井降深。干扰作用使各个井的降落漏斗叠在一起而形成大面积的区域降落漏斗。在供水工程和排水（疏干）工程中，常根据需要规定降深，计算各井的涌水量及井群的总涌水量及降深。

井群的干扰程度一方面受含水层性质、补给、排泄等条件的影响；另一方面也受井的数量、井的间距、布置方式、井到边界的距离等因素的影响，在设计时都应考虑到。一般说，在同一含水层中，井越多，出水量越大；井间距越小，水位降深越大。对于供水井群应从合理的技术及经济效益出发，以少量的井达到流量大的效果；对于排水井群应以少量井达到降深大的效果。

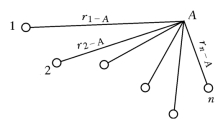
图4-18　干扰井群

地下水向干扰井群稳定运动的计算公式，是以单井的裘布依公式为基础，根据叠加原理来建立的。叠加原理可简述为：干扰井群工作时，于任一点处产生的降深值，等于各井单独工作时于该点处产生降深值的代数和。

（一）任意排列的干扰井群

设在一无限的水平含水层中有n口完整井，按任意方式排列并相互干扰（图4-18）。各井的干扰抽水量为Q1-A、Q2-A，…，Qn，井群影响范围内有任意计算点A，各井到A点的距离为r1，r2，…，rn-A。当各井同时工作，按叠加原理，计算点A的总降深是各井单独工作时在A点产生的降深之和：

对于承压井群：

为简化起见，设

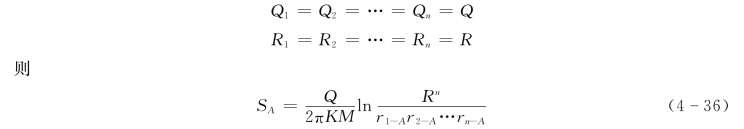
承压井群中任一井的单井流量

潜水井群中任一井的单井流量

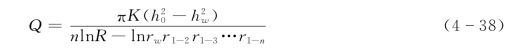
式中　Sw，rw——任一井中的水位降深和井的半径；

　　　r1-2，r1-3，…，r1-n——该井至其余各井的距离。

干扰井群的总流量

在排水疏干设计时，常常要计算含水层内任意点A的动水位，以检查水位降深是否达到要求，如降深不够，可增加抽水量或增加排水井。具体计算如下：

承压井群

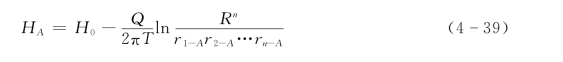
潜水井群

（二）环状排列的干扰井群

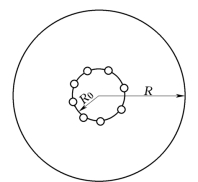
在上述条件下井群按半径为R0的圆周均匀布置（如图4-19）。设每口井的抽水量相等，即Q=Q1=Q2=…=Qn。当计算点A取在井群中任意一口井的井壁上，根据几何关系可知：rwr1-1，r2-1，…，rn-1=rwnRn0-1，在上述简化条件下，由式（4-37）和式（4-38）两式可得近似公式如下：

承压井群中任一井

(www.daowen.com)

图4-19　环状排列的干扰井群

潜水井群中任一井

当井数较多，环状排列较密，可视井群为以R0为半径的“大井”，其总出水量Q如下：

承压完整井群

潜水完整井群

（三）矩形排列的干扰井群

井群排列成方形或矩形时，设井群中心的降深为Sw，这样每一个单井的降深必然比它大。这时将矩形排列的井群看成是以R0为半径的大井。干扰井群的总流量Q的计算公式如下：

承压完整井群

潜水完整井群

式中　hw——与Sw相应的井群中心含水层厚度。

大井半径R0的确定：

井群按圆形排列时，大井半径就是圆形的半径；

井群不规则或其他形状排列时，可按下式计算引用半径R0

式中　F——井群排列线范围内的面积，m2。

如果井群排列为狭长的矩形，可用下式计算

式中　l、b——矩形的长和宽，m；

　　　η——系数，按表4-3确定。

表4-3　狭长的矩形排列井群系数计算表